 |
2.4. Зміст розрахункової роботи
|
|
|
|
2. 4. Зміст розрахункової роботи
Для плоского перерізу, складеного з прокатних профілів, потрібно визначити положення головних центральних осей. Знайти значення моментів інерції перерізу, а також моментів опору перерізу та радіусів інерції відносно цих осей.
Приклад виконання розрахункової роботи
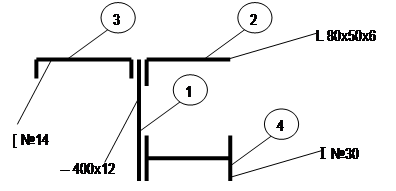 |
Задано переріз, що складається з чотирьох профілів: листа - 1, нерівнобокого кутника - 2, швелера - 3, двотавра - 4. Схема перерізу з номерами профілів приведена на рис. 2. 1.
Рис. 2. 1
1. Виписуємо зі сортамента прокатних профілів необхідні розміри елементів (у сантиметрах) та величини геометричних характеристик перерізу. Заносимо в таблицю вихідних даних 2. 1.
У тому разі, коли положення перерізу в завданні не відповідає розташуванню його в сортаменті прокатних профілів, вносимо зміни до величини геометричних характеристик.
Наприклад:
а) Нерівнобокий кутник: L 80х50х6
| Сортамент | Завдання | ||
|
|
F = 7, 55 см2 х0 = 1, 17 см у0 = 2, 65 см |
| |
 14. 8 см4 14. 8 см4
 = 49 см4 = 49 см4
| F = 7, 55 см2 х0 =2, 65 см у0 = 1, 17 см | ||
Рис. 2. 2
б) Швелер: № 14
| Сортамент | Завдання | ||||||
  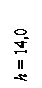   
|
F = 15. 6 см2 х0 =1. 67 см у0 = 0 см |
| |||||
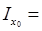 45. 4 см4 45. 4 см4
 = 491 см4 = 491 см4
| F = 15. 6 см2 х0 = 0 см у0 = 1. 67 см | ||||||
Рис. 2. 3
в) Двотавр: № 30
| Сортамент | Завдання | ||
|
|
F = 46. 5 см2
|
| |
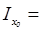 337 см4 337 см4
 = 7080 см4 = 7080 см4
| F = 46. 5 см2 | ||
Рис. 2. 4
Моменти інерції листа визначаємо так:
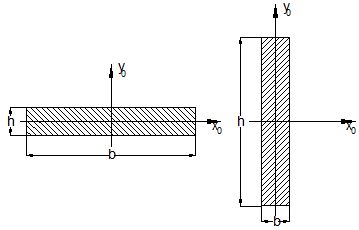
|  (2. 7) (2. 7)
 (2. 8)
h = 40 см,
b = 1, 2 см (2. 8)
h = 40 см,
b = 1, 2 см
|
Рис. 2. 5
У таблиці сортаменту для нерівнобокого кутника приведені значення мінімального моменту інерції Imin та кута a нахилу осі min, необхідні для визначення відцентрового моменту інерції.
|
|
|
Величину Imax для нерівнобокого кутника знаходимо з умови:
 +
+  = Imin+ Imax
= Imin+ Imax
Звідси
Iymax =  +
+  - Imin (2. 9)
- Imin (2. 9)
2. Заданий поперечний переріз зображуємо в масштабі (рис. 2. 6).
Для кожного елемента перерізу показані власні центральні осі та розміри, що визначають положення центрів ваги Сі окремих профілів.
3. Визначаємо координати центру ваги усього перерізу. За допоміжну систему координат приймемо осі х1 у1, що проходять через центр ваги листа. При такому виборі допоміжної системи обчислення декілька спрощуються.
Координати центру ваги перерізу визначаються за формулами (2. 1):
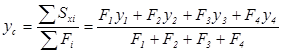

де Sxi, Syj - статичні моменти площі перерізів окремих фігур;
хi, уі - координати центрів ваги окремих фігур у допоміжній системі координат.
За допомогою рис. 2. 6 знайдемо:
х1 = 0;
х2 = 2, 65 + 0, 6 = 3, 25 см,
х3 = -(7 + 0, 6) = -7, 6см;
х4 = 15 + 0, 6 = 15, 6см;

у2 = 40/2 – 1, 17 = 18, 8 см
у3 = 40/2 – 1, 67 = 18, 33 cм
у4 = - (40/2 – 6, 75) = -13, 25 см
Обчислення проводимо в табличній формі (див. табл. 2. 2). Знайдені значення координат заносимо в стовбці 3, 4 таблиці. У стовбцях 5, 6 обчислюються значення статичних моментів окремих профілів і всього перерізу. За формулами (2. 4) маємо
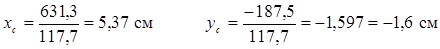
Таблиця 2. 1.
Вихідні дані завдання.
|
№ п/п |
Розмір перерізу |
F, см2 | Центр ваги у власних осях (см) |
Ixo см4 |
Iyo см4 |
Imin см4 |
Imax см4 |
b см |
tga | |
| х0 | у0 | |||||||||
| -40x1, 2 | - | - | 5, 8 | - | - | - | - | |||
| L8x5x0, 6 | 7, 55 | 2, 55 | 1, 17 | 14, 8 | 8, 9 | 54, 92 | - | 0, 386 | ||
| [ № 14 | 15, 6 | - | 1, 67 | 45, 4 | 49, 1 | - | - | 5, 8 | - | |
| I № 30 | 46, 5 | - | - | - | - | 13, 5 | - | |||
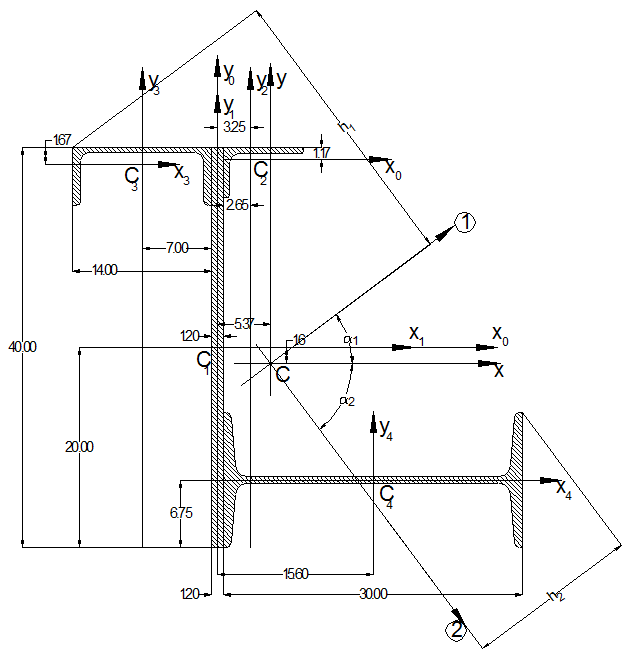
Рис. 2. 6 (М 1: 4)
|
Таблица 2. 2
| ||||||||||||||||||||
| № п/п | Fi (см2) | yi (см) | xi (см) | Sxi (см3) | Syi (см3) | ai=yi-yc | bi=xi-xc | Перевірка | Ixi (см4) | ai2Fi (см4) | Ixc (см4) | Iyi (см4) | bi2Fi (см4) | Iyc (см4) | Ixiyi (см4) | aibiFi (см4) | Ixcyc (см4) | |||
| Sxi=aiFi | Syi=biFi | |||||||||||||||||||
| 1. 59 | -5. 36 | 76. 3 | -257. 3 | 5. 8 | -410 | -410 | ||||||||||||||
| 7. 55 | 18. 83 | 3. 25 | 142. 7 | 24. 5 | 20. 42 | -2. 11 | 154. 2 | -15. 9 | 14. 8 | 15. 5 | -328 | -312 | ||||||||
| 15. 6 | 18. 33 | -7. 6 | 285. 9 | -118. 6 | 19. 92 | -12. 9 | 310. 8 | -201. 2 | 45. 4 | -4030 | -4030 | |||||||||
| 46. 5 | -13. 25 | 15. 6 | -616. 7 | 725. 4 | -11. 66 | 10. 24 | -542. 2 | 476. 2 | -5547 | -5547 | ||||||||||
| 117. 7 | -187. 5 | 631. 3 | -0. 9 | 1. 8 | -10310 | |||||||||||||||
0, 17% 0, 38%
Наносимо на рис. 2. 6 координати центру ваги С усього перерізу і проводимо через нього центральні осі х і у. Знайдемо координати центрів ваги окремих фігур у новій системі координат:
ai = уci - уc, bi = хci - хc (2. 9)
Результати цих обчислень за формулами (2. 6) заносимо в стовбці 7, 8 табл. 2. 2.
Для перевірки правильності обчислень координат центру ваги необхідно порахувати статичні моменти площі перерізу відносно осей х и у:
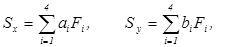 (2. 10)
(2. 10)
які повинні дорівнювати нулю.
Згідно зі стовбцями 9, 10 табл. 2. 2 відносні похибки рівні:

4. Обчислимо осьові та відцентрові моменти інерції усього перерізу відносно центральних осей х, у за формулами (2. 2)
Обчислення за формулами (2. 2) заносяться в стовбці 11-19 табл. 2. 2.
Відцентровий момент інерції кутника  обчислюється слідуючим чином. На рис. 2. 7. показано кутник і його головні центральні осі 1, 2.
обчислюється слідуючим чином. На рис. 2. 7. показано кутник і його головні центральні осі 1, 2.
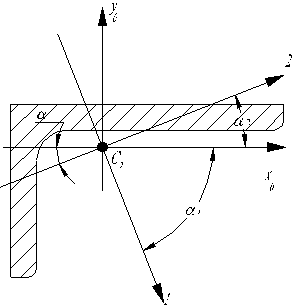 |
Рис. 2. 7
Для нерівнобокого і рівнобокого кутників осі х та у не є головними, тому відцентровий момент інерції для цих фігур обчисляється за формулами (2. 4).
Звідси

 (2. 11)
(2. 11)
Відповідно до рисунка 2. 7
tga2 = tga = 0, 386
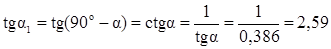
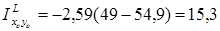 см4
см4  = 0, 386(49-8, 9)=15, 4см4
= 0, 386(49-8, 9)=15, 4см4
Для рівнобокого кутника a1 = a2 = 45о, tgai = ±1.
Таким чином для всього перерізу маємо (див. табл. 2. 2):
Ix = 22596 см4, Iy = 16534 см4, Ixy = -10310см4.
|
|
|
5. Обчислимо головні центральні моменти інерції всього перерізу за формулами (2. 3):
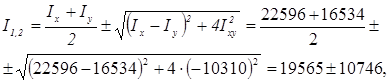
I1 = 30311см4, I2 = 8819см4
6. Визначаємо положення головних центральних осей 1 і 2 відносно центральної осі х:
 = 360 47’
= 360 47’
 = -530 21’
= -530 21’
Кут a1 визначає положення головної осі з максимальним моментом інерції, а кут a2 – з мінімальним.
Відкладаємо за допомогою транспортира головні осі 1 (a1) і 2 (-a2), (рис. 2. 6).
7. Перевірки:
а) Інваріантність моментів інерції
Ix + Iy = I1 + I2
22596 + 16534 = 30311 + 8819
39130 = 39130
б) Екстремальність моментів інерції:
I1 > Ix > Iy > I2
30311 > 22596 > 16534 > 8819
аналогічно
I2 < Iy < Ix < I1
в) Перпендикулярність головних осей 1 і 2:
|a1| + |a2| = p/2
36, 790 + 53, 210 = 900 = p/2.
8. Обчисляємо розміри моментів опору відносно головних центральних осей інерції 1, 2 за формулами (2. 5):
 см3
см3  см3
см3
h1max та h2max - визначаються з урахуванням масштабу згідно рисунка 2. 6.
9. Радіуси інерції відносно головних центральних осей визначаються за формулами (2. 6)
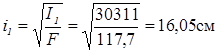
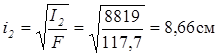
|
|
|




 49 см4
49 см4 = 14. 8 см4
= 14. 8 см4
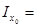 491 см4
491 см4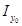 = 45. 4 см4
= 45. 4 см4

