 |
5.4.2. Зміст задачі на позацентровий стиск.
|
|
|
|
5. 4. 2. Зміст задачі на позацентровий стиск.
Для короткого стояка потрібно:
- визначити координати центру ваги, виразивши всі величини через характерні розміри перерізу; обчислити головні моменти і квадрати радіусів інерції заданого перерізу;
- знайти відрізки, що відсікаються на головних осях інерції, нейтральною лінією та побудувати її;
- з умови міцності матеріалу на розтяг і стиск визначити розміри поперечного перерізу, якщо Rст - розрахунковий опір матеріалу на стиск, Rpозт - те ж, на розтяг;
- знайти нормальні напруження у характерних точках перерізу стояка і побудувати епюру s в аксонометрії;
- побудувати ядро перерізу.
Приклад розрахунку короткого стояка на позацентровий стиск
Для стояка, завантаженого в точці I силою Р = 1, 0 МН, визначити розміри перерізу при Rст = - 200 МПа, Rpозт = 75 МПа, b/h =7/16 (рис. 5. 8, а).
1. Розбиваємо заданий переріз на прості площі F1, F2, F3 з показом власних центральних осей xi, yi (i=1, 2, 3) (Рис. 5. 8, б)
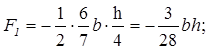® D EGF
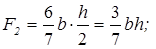® EGKD
® BLHA
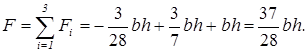
2. Координати центрів ваги складових площ щодо допоміжної осі х0:
3. Обчислення координати центру ваги, що лежить на осі симетрії у:
Головні центральні осі х, у показані на рис. 5. 9.
 |
Рис. 5. 8
4. Обчислення значень квадратів радіусів інерції 
відносно головних центральних осей х, у.
, 
5. Визначення положення нейтральної лінії відрізками, які відсікає вона на головних центральних осях інерції за формулами (5. 6):
, 
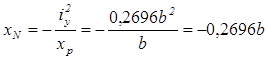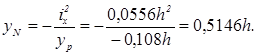
На рис. 5. 10 показано положення нейтральної лінії. Нейтральна лінія поділяє переріз на дві зони: в однієї виникають розтягуючі напруження, а у другій – стискаючі. Очевидно, що в стиснутій зоні небезпечною є точка Н, а в розтягнутій – точка В. З умови міцності матеріалу в цих точках визначимо необхідні розміри b і h перерізу короткого стояка.
|
|
|
6. Визначення розмірів поперечного перерізу з умови міцності:
а) 
£ Rст
або
£ Rст
відкіля при 
: 
£ Rст.
Відкіля 
см
см.
б) 
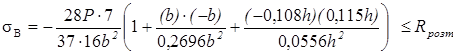
см.
Остаточно приймаємо розміри b = b(2) = 11, 5 см, h = h(2) = 26, 50 см.
7. Визначення нормальних напружень у кутових точках контуру поперечного перерізу стояка і побудова епюри напружень в аксонометрії. Застосовуємо формулу (5. 4*)
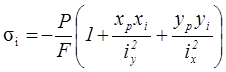
Так для точки B маємо:
Для точки Н одержуємо:
= -134, 2 МПа < Rст =200МПа
Аналогічно знаходимо нормальні напруження в інших кутових точках та заносимо до таблиці 5. 1 при хр = b = 11, 5 см; ур = - 0, 108h = - 2, 862 см;
.
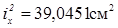Таблиця 5. 1
|
Точки | Координати точки, де знаходиться Р=1МН | Координаты характерних точок (i) | Напруження s, МПа | ||
| хр, см | ур, см | х, см | у, см | ||
| A |
11, 5 |
-2, 862 | -11, 5 | -9, 487 | 50, 00 |
| B | -11, 5 | 3, 763 | 74, 12 | ||
| D | -4, 9335 | 3, 763 | 21, 53 | ||
| E | -4, 9335 | 17, 013 | 45, 645 | ||
| F | 0, 0 | 10, 388 | -6, 014 | ||
| G | 4, 9335 | 17, 013 | -33, 376 | ||
| K | 4, 9335 | 3, 763 | -57, 492 | ||
| L | 11, 5 | 3, 763 | -110, 08 | ||
| H | 11, 5 | -9, 487 | -134, 20 | ||
 |
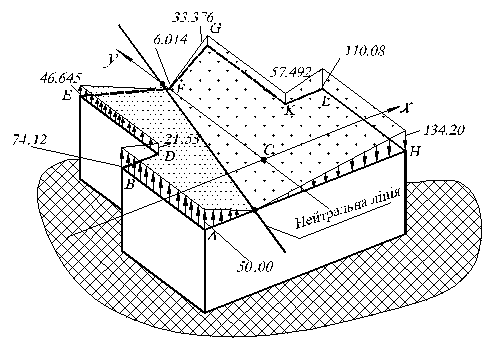Епюра нормальних напружень представлена на рис. 5. 9.
Рис. 5. 9
Напруження - у МПа.
 |
8. Побудова ядра перерізу. Задаємось положеннями дотичних ліній (рис. 5. 10):
Рис. 5. 10
а) дотична лінія I-I ~ АВ; відрізкі які дотична відсікає на координатних осях: ах = -11, 5 см, ау Þ ¥
За формулами (5. 7) одержуємо:
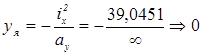
б) дотична лінія II-II проходе через точки В и Е.
За формулами (5. 9) и (5. 10) отримуємо:
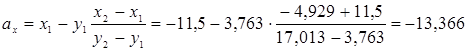см
см
см, 
см.
в) дотична лінія III-III між точками Е и G.
ах Þ ¥, ау = 17, 013 см
хя = 0,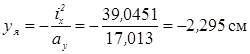 
|
|
|
г) дотична лінія IV-IV між точками А и Н.
ах Þ ¥, ау = -9, 487 см,
хя = 0, 
Точки 1¢, 2¢ розташовані симметрично точкам 1, 2 відносно осі у. Таким чином з’єднавши точки 1, 2, 3, 4, 2¢, 3¢ прямими одержуємо ядро перерізу, що заштриховано на рис. 5. 10.
РОЗРАХУНКОВО-ПРОЕКТУВАЛЬНА РОБОТА №6
Розрахунок центрально-стиснутих стержнів на стійкість
6. 1. Питання до самостійної роботи
1. У чому полягає явище втрати стійкості стисненого стержня?
2. Що називається критичною силою і критичним напруженням?
3. Як впливає жорсткість поперечного перерізу і довжина стержня на величину критичної сили?
4. Що являє собою коефіцієнт приведення довжини і чому він дорівнює при різноманітних умовах закріплення кінців стержня?
5. Який критерій застосування формули Ейлера?
6. Як визначаються критичні напруження за формулою Ясинського?
7. Який вигляд має умова міцності при поздовжньому згині стисненого стержня?
8. Що являє собою коефіцієнт поздовжнього згину, як визначається його значення?
9. Як визначити коефіцієнт запасу стійкості?
|
|
|
