 |
6.2. Стислі теоретичні зведення
|
|
|
|
6. 2. Стислі теоретичні зведення
Розрізняють стійкий, байдужний та нестійкий стани рівноваги. Навантаження, що відповідає граничному значенню байдужного стана рівноваги довгого стисненого стержня, називається критичним. Перевищення цього значення навантаження призводить до нестійкої рівноваги елемента або до його руйнування.
Розмір критичного навантаження визначається за формулою Л. Ейлера в тому випадку, коли максимальна гнучкість 
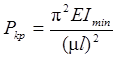 , або
, або  (6. 1)
(6. 1)
Критичне навантаження визначається за емпіричною формулою Ф. С. Ясинського для значень максимальної гнучкості (40 ¸ 50) £ lmax < 104:
Ркр = sкр · F, де (6. 2)
sкр = a - bl; (6. 3)
Емпіричні коефіцієнти а і b визначаються по довідковим даним у залежності від матеріалу елемента.
Так для Ст. 3 - а = 310 МПа, b = 1, 14 МПа (6. 4)
Значення критичного навантаження Ркр залежить від довжини стояка l, умов закріплення його кінців (коефіцієнт m), а також форми і розмірів поперечного перерізу (мінімальний радіус інерції i). Тут і далі використовується поняття гнучкості елемента 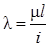 . Чим більше гнучкість, тим менше величина Ркр. Тому що критичну силу Ркр в елементах конструкцій допускати не можна. Допустиме навантаження на стиснений стояк визначається:
. Чим більше гнучкість, тим менше величина Ркр. Тому що критичну силу Ркр в елементах конструкцій допускати не можна. Допустиме навантаження на стиснений стояк визначається:
[P] = Pкр/k (6. 5)
де k > 1 - коефіцієнт запасу стійкості.
Умова стійкості при поздовжньому згині записується у вигляді:
 , (6. 6)
, (6. 6)
|
|
|
j - коефіцієнт зниження розрахункового опору при поздовжньому згині. Визначається за таблицями у залежності від гнучкості l та конкретним матеріалом стояка. Така таблиця наведена для сталі з розрахунковим опором R=205МПа (таблиця 6. 1).
Формула (6. 6) містить дві невідоміх величини F та j. Тому задача підбора поперечного перерізу при поздовжньому згині вирішується методом послідовних наближень.
6. 3. Порядок виконання роботи
1. Задаємось значенням j = 0, 5 і підбираємо розміри поперечного перерізу елемента.
2. Розташовуємо заданий поперечний переріз стояка найбільш раціонально щодо умов закріплення в двох взаємно перпендикулярних площинах.
3. У площині найбільшої гнучкості, де Ркр має найменше значення, підбираємо розміри поперечного перерізу стояка.
4. Визначаємо розмір розрахункових напружень матеріалу стояка при прийнятих розмірах перерізу.
5. Визначаємо розмір критичної сили та коефіцієнт запасу стійкості.
6. 4. Зміст роботи
Для стояка з заданою формою поперечного перерізу і закріпленого відповідно до завдання потрібно:
1. Розташувати поперечний переріз елемента найбільш раціонально щодо умов закріплення в двох взаємно перпендикулярних площинах.
2. Підібрати розміри поперечного перерізу елемента, якщо розрахунковий опір матеріалу R = 205 МПа, модуль пружності Е =  МПа.
МПа.
3. Обчислити значення критичної сили та коефіцієнта запасу на стійкість.
Таблица 6. 1
Коеффициенты j продольного изгиба центрально-сжатых элементов
Сталь Ry=205 МПа, E=2. 06*105 МПа
СНиП II-23-81* Стальные конструкции
| l | ||||||||||
| 0. 9882 | 0. 9864 | 0. 9845 | 0. 9826 | 0. 9805 | 0. 9784 | 0. 9762 | 0. 9739 | 0. 9716 | 0. 9692 | |
| 0. 9667 | 0. 9642 | 0. 9616 | 0. 9590 | 0. 9563 | 0. 9535 | 0. 9507 | 0. 9478 | 0. 9449 | 0. 9419 | |
| 0. 9389 | 0. 9358 | 0. 9327 | 0. 9295 | 0. 9263 | 0. 9230 | 0. 9197 | 0. 9163 | 0. 9129 | 0. 9094 | |
| 0. 9059 | 0. 9023 | 0. 8988 | 0. 8951 | 0. 8914 | 0. 8877 | 0. 8839 | 0. 8801 | 0. 8763 | 0. 8724 | |
| 0. 8685 | 0. 8645 | 0. 8605 | 0. 8565 | 0. 8524 | 0. 8483 | 0. 8441 | 0. 8399 | 0. 8357 | 0. 8314 | |
| 0. 8271 | 0. 8228 | 0. 8184 | 0. 8140 | 0. 8095 | 0. 8051 | 0. 8005 | 0. 7960 | 0. 7914 | 0. 7868 | |
| 0. 7821 | 0. 7775 | 0. 7727 | 0. 7680 | 0. 7632 | 0. 7584 | 0. 7535 | 0. 7487 | 0. 7438 | 0. 7388 | |
| 0. 7338 | 0. 7289 | 0. 7217 | 0. 7145 | 0. 7073 | 0. 7002 | 0. 6932 | 0. 6861 | 0. 6792 | 0. 6722 | |
| 0. 6654 | 0. 6585 | 0. 6517 | 0. 6449 | 0. 6382 | 0. 6316 | 0. 6249 | 0. 6183 | 0. 6118 | 0. 6053 | |
| 0. 5988 | 0. 5924 | 0. 5860 | 0. 5797 | 0. 5734 | 0. 5672 | 0. 5610 | 0. 5548 | 0. 5487 | 0. 5426 | |
| 0. 5366 | 0. 5306 | 0. 5247 | 0. 5188 | 0. 5129 | 0. 5071 | 0. 5013 | 0. 4956 | 0. 4899 | 0. 4843 | |
| 0. 4787 | 0. 4731 | 0. 4676 | 0. 4622 | 0. 4567 | 0. 4513 | 0. 4460 | 0. 4407 | 0. 4355 | 0. 4302 | |
| 0. 4251 | 0. 4199 | 0. 4149 | 0. 4098 | 0. 4048 | 0. 3999 | 0. 3950 | 0. 3901 | 0. 3853 | 0. 3805 | |
| 0. 3757 | 0. 3710 | 0. 3664 | 0. 3618 | 0. 3572 | 0. 3499 | 0. 3454 | 0. 3409 | 0. 3365 | 0. 3323 | |
| 0. 3281 | 0. 3240 | 0. 3199 | 0. 3160 | 0. 3121 | 0. 3083 | 0. 3045 | 0. 3009 | 0. 2973 | 0. 2938 | |
| 0. 2903 | 0. 2869 | 0. 2836 | 0. 2803 | 0. 2771 | 0. 2739 | 0. 2708 | 0. 2677 | 0. 2647 | 0. 2618 | |
| 0. 2589 | 0. 2561 | 0. 2533 | 0. 2505 | 0. 2478 | 0. 2452 | 0. 2425 | 0. 2400 | 0. 2374 | 0. 2350 | |
| 0. 2325 | 0. 2301 | 0. 2277 | 0. 2254 | 0. 2231 | 0. 2209 | 0. 2187 | 0. 2165 | 0. 2143 | 0. 2122 | |
| 0. 2101 | 0. 2081 | 0. 2061 | 0. 2041 | 0. 2021 | 0. 2002 | 0. 1983 | 0. 1964 | 0. 1946 | 0. 1928 | |
| 0. 1910 | 0. 1892 | 0. 1875 | 0. 1857 | 0. 1841 | 0. 1824 | 0. 1808 | 0. 1791 | 0. 1775 | 0. 1760 | |
| 0. 1744 | 0. 1729 | 0. 1714 | 0. 1699 | 0. 1684 | 0. 1670 | 0. 1656 | 0. 1642 | 0. 1628 | 0. 1614 | |
| 0. 1600 | 0. 1587 | 0. 1574 | 0. 1561 | 0. 1548 | 0. 1536 | 0. 1523 | 0. 1511 | 0. 1499 | 0. 1487 |
|
|
|
6. 5. Приклад виконання розрахункової роботи
ЗАДАЧА 1
Дано: Р = 1000 кН, l= 4 м, R = 205 МПа, Е =  МПа. Переріз стержня складено з чотирьох однакових швелерів. Форма перерізу й умови закріплення кінців стержня приведені на рис. 6. 1а.
МПа. Переріз стержня складено з чотирьох однакових швелерів. Форма перерізу й умови закріплення кінців стержня приведені на рис. 6. 1а.
1. Задаємося значенням j1 = 0, 5 та визначаємо потрібну площу поперечного перерізу швелера:
F(1) = 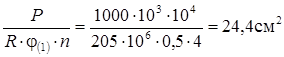
Приймаємо 4 [ № 20. Геометричні характеристики за сортаментом для кожного складають:
 = 23, 4 см2, Ix = 1520 см4, Iy = 113 см4, х0 = 2, 07 см.
= 23, 4 см2, Ix = 1520 см4, Iy = 113 см4, х0 = 2, 07 см.
Моменти інерції щодо головних центральних осей х і у перерізу (рис. 6. 1а):

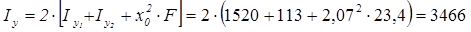 см4
см4
F = 4 · 23, 4 = 93, 6 см.
Радіуси інерції:

2. Визначаємо раціональне розташування перерізу для двох варіантів (рис. 6. 1, б):
I варіант:
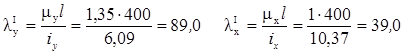
II варіант:

З огляду на те, що розрахунок ведеться по максимальній гнучкості, у першому варіанті втрата стійкості буде відносно осі y, у другому - відносно осі x.
|
|
|
З двох варіантів розташування перерізу найбільш раціональним є другий, тому що

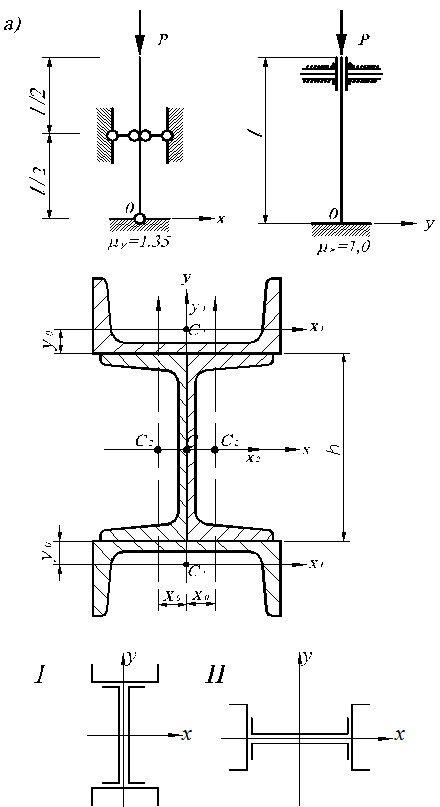 |
Рис. 6. 1
3. Приймаємо другий варіант і розрахунок ведемо відносно осі х (рис. 6. 1. а):
lх = 66, 0 за таблицею 
Друге наближення:
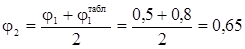
F(2) =  18, 76 см2
18, 76 см2
Приймаємо 4 [ № 16 F = 18, 1см2, Iх = 747 см4, Iу = 63, 0 см4, х0 = у0 = 1, 8 см.

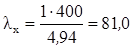

Третє наближення:
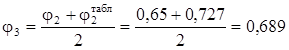
Аналогічно далі F3 = 17, 70 см2.
Приймаємо 4[№ 16 (F = 18, 1см2, Iх = 747 см4, Iу = 63, 6 см4, х0 = 1, 8 см).
ix = 4, 94 см, lх = 81, 0,  = 0, 727.
= 0, 727.
4. Визначаємо розрахункові напруження у матеріалі стояка:
 МПа < R = 205 МПа
МПа < R = 205 МПа
Таким чином, остаточно приймаємо переріз стояка з 4 швелерів за № 16.
5. Визначаємо величину критичної сили та коефіцієнт запасу на стійкість. Тому що в останньому наближенні lх=81, 6 < 104 - критичне навантаження визначаємо за формулою Ясинського:
Ркр = sкр·F =(310-1, 14lх)·4·106·F=(310-1, 14·81, 6)·4·18, 1·10-4=1, 576МH=1576 кН
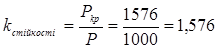
ЗАДАЧА 2
Дано: Р = 200 кН, l = 2 м, R = 205 МПа, Е =  МПа. Поперечний переріз стержня має характерний розмір “а”, та послаблений отвором прямокутної форми (рис. 6. 2, а). Умови закріплення кінців стержня приведені на рис. 6. 2, а.
МПа. Поперечний переріз стержня має характерний розмір “а”, та послаблений отвором прямокутної форми (рис. 6. 2, а). Умови закріплення кінців стержня приведені на рис. 6. 2, а.
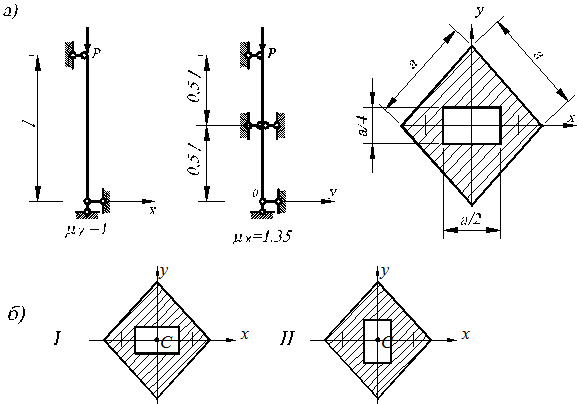 |
Рис. 6. 2
1. Визначаємо геометричні характеристики заданого поперечного перерізу:
F = a · a - 0, 5a · 0, 25a = 0, 875 a2
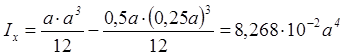

Радіуси інерції:

2. Визначаємо раціональне розташування перерізу для двох варіантів (рис. 6. 2 б):
I варіант:

II варіант:
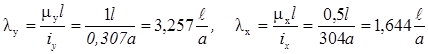
Таким чином вигіднішим є варіант II. Розрахунок ведемо відносно осі у за другим варіантом.
3. Визначаємо аналітичну залежність між гнучкістю l і коефіцієнтом j:


lу = 195, 1 
I спроба: j1 = 0, 5, lу = 195, 1  = 138, j1= 0, 386.
= 138, j1= 0, 386.
II спроба: 
III спроба: 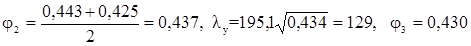
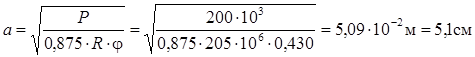
4. Розрахункове напруження:
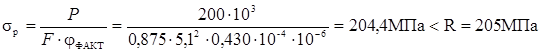 .
.
Остаточно приймаємо характерний розмір поперечного перерізу стояка а = 5, 1 см.
5. Визначаємо величину критичної сили і коефіцієнт запасу на стійкість:
lу =129 > 100. Критичну силу визначаємо за формулою Ейлера:

Коефіцієнт запасу стійкості визначаємо із співвідношення:
|
|
|

|
|
|


