 |
Геометрический смысл производной
|
|
|
|
Геометрический смысл производной
Вспомним, что производная — это скорость изменения функции.
Производная функции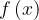 
в точке 
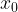равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.
1. На рисунке изображён график функции 
и касательная к нему в точке с абсциссой 
Найдите значение производной функции 
в точке
Производная функции в точке 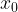равна тангенсу угла наклона касательной, проведенной в точке .
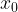Достроив до прямоугольного треугольника АВС, получим:
Ответ: 0, 25.
2. На рисунке изображён график функции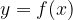 
и касательная к нему в точке с абсциссой
Найдите значение производной функции 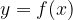в точке
Начнём с определения знака производной. Мы видим, что в точке 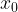функция убывает, следовательно, её производная отрицательна. Касательная в точке 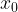образует тупой угол 
с положительным направлением оси 
. Поэтому из прямоугольного треугольника мы найдём тангенс угла 
, смежного с углом .
Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: 
Поскольку 
, имеем:
Ответ: − 0, 25.
Касательная к графику функции
3. Прямая 
является касательной к графику функции 
Найдите абсциссу точки касания.
Запишем условие касания функции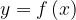 
и прямой 
в точке
При 
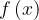значения выражений и 
равны.
При этом производная функции 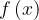равна угловому коэффициенту касательной, то есть 
.
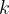Из второго уравнения находим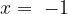 
или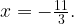 
Первому уравнению удовлетворяет только 
.
Физический смысл производной
Мы помним, что производная — это скорость изменения функции.
Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.
|
|
|
Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.
4. Материальная точка движется прямолинейно по закону 
, где 
— расстояние от точки отсчета в метрах, 
— время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени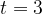 
с.
Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета: 
Найдем скорость материальной точки как производную от координаты по времени:
В момент времени 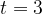получим:
.
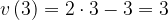Ответ: 3
Применение производной к исследованию функций
Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.
Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.
Или наоборот. Нарисован график производной — а спрашивают о поведении функции.
И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.
Если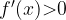 
, то функция возрастает.
Если 
, то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
|
| возрастает | точка максимума | убывает | точка минимума | возрастает |
| 
| 
|
|
5. На рисунке изображен график функции 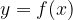, определенной на интервале 
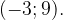Найдите количество точек, в которых производная функции равна 0.
|
|
|
Производная функции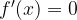 
в точках максимума и минимума функции 
Таких точек на графике 5.
Ответ: 5.
6. На рисунке изображён график 
— производной функции , определённой на интервале 
. В какой точке отрезка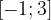 
функция принимает наибольшее значение?
Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?
Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.
На отрезке 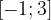производная функции положительна.
Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.
Ответ: 3.
7. На рисунке изображён график функции 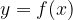, определённой на интервале 
. Найдите количество точек, в которых касательная к графику функции параллельна прямой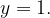 
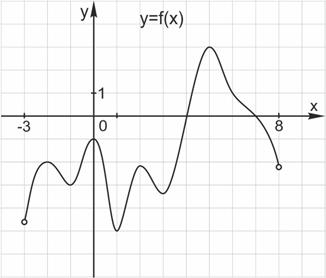
Прямая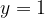 
параллельна оси абсцисс. Найдем на графике функции 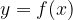точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.
Ответ: 7.
8. На рисунке изображен график производной функции , определенной на интервале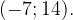 
Найдите количество точек максимума функции на отрезке 
Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке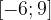 
такая точка всего одна! Это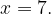 
Ответ: 1.
9. На рисунке изображен график производной функции , определенной на интервале 
Найдите точку экстремума функции на отрезке 
Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке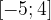 
график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке 
В этой точке производная меняет знак с минуса на плюс.
Значит,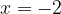 
является точкой экстремума.
|
|
|
