 |
Задачи для самостоятельной работы
|
|
|
|
Задачи для самостоятельной работы
12. 1. Случайная величина X задана плотностью распределения вероятностей 
; 
; 
. Найти ее характеристическую функцию.
12. 2. Найти преобразование Лапласа и начальные моменты двух первых порядков случайной величины X, имеющей равномерное распределение на интервале [2, 4].
12. 3. Величины X и Y независимы и одинаково распределены с преобразованием Лапласа 
. Найти преобразование Лапласа величин Z=X+Y и T=X-Y.
12. 4. Найти преобразование Лапласа случайной величины X, заданной плотностью распределения вероятностей 
, .
12. 5. Найти характеристическую функцию и начальные моменты случайной величины, плотность распределения вероятностей которой имеет следующий вид
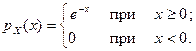
12. 6. Случайная величина X имеет плотность распределения вероятностей
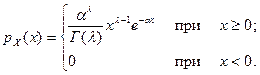
Найти ее производящую функцию семиинвариантов, математическое ожидание и дисперсию.
12. 7. Найти характеристическую функцию, математическое ожидание и дисперсию случайной величины X, плотность распределения вероятностей которой (закон арксинуса) имеет вид 
.
12. 8. Найти характеристическую функцию случайной величины X, распределенной по закону Коши 
.
12. 9. Случайная величина X задана характеристической функцией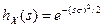 
. Найти все центральные моменты этой величины.
12. 10. Случайная величина X задана характеристической функцией 
. Определить плотность распределения вероятностей величины X.
12. 11. Является ли характеристической функцией распределения вероятностей функция 
.
12. 12. Найти математическое ожидание и дисперсию случайной величины X, характеристическая функция которой имеет вид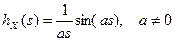 
.
12. 13. Найти производящую функцию семиинвариантов, математическое ожидание и дисперсию, асимметрию и эксцесс случайной величины X, заданной характеристической функцией 
.
|
|
|
12. 14. Независимые случайные величины X и Y заданы характеристическими функциями: 
; 
. Найти распределение величины Z=X+Y.
12. 15. Для случайной величины, заданной плотностью распределения вероятностей 
, найти производящую функцию семиинвариантов.
12. 16. Найти производящую функцию семиинвариантов, математическое ожидание и дисперсию случайной величины X, заданной распределением Максвелла 
.
12. 17. Найти правостороннее преобразование Лапласа и начальные моменты случайной величины X, заданной функцией распределения вероятностей 
.
12. 18. Найти плотность распределения вероятностей и правостороннее преобразование Лапласа случайной величины X, заданной характеристической функцией 
.
12. 19. Независимые случайные величины X, Y и Z заданы производящими функциями семиинвариантов 
; c – целое положительное число. Найти константу c и характеристическую функцию величины Q=X+Y+Z.
12. 20. Найти коэффициенты асимметрии и эксцесса случайной величины X, заданной характеристической функцией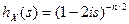 
, n – целое положительное число.
12. 21. Случайные величины X и Y независимы и равномерно распределены на отрезке [a, b]. Найти характеристическую функцию величины Z=X+Y.
13. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Основные понятия и теоремы раздела
Последовательность случайных величин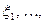 
называется сходящейся по вероятности к случайной величине 
, если для любого e > 0 имеет место равенство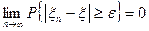 
. Кратко такой вид сходимости записывается следующим образом: 
.
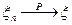Последовательность случайных величин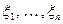 
называется сходящейся с вероятностью единица (почти наверное (п. н. ), или почти всюду (п. в. )) к случайной величине , если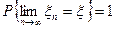 
. Краткие обозначения: 
, 
, 
.
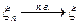Последовательность случайных величин называется сходящейся в среднем порядка r к случайной величине , если 
. Кратко такая сходимость записывается следующем виде: 
. В том частном случае, когда r = 2, эту сходимость называют сходимостью в средне квадратическом и обозначают так: 
.
|
|
|
Последовательность случайных величин 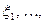называется сходящейся к случайной величине по распределению, если 
в каждой точке непрерывности функций распределения 
, 
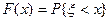. Сокращенно этот вид сходимости отображается следующим образом: 
.
Связь между различными видами сходимости можно изобразить следующим образом:
Здесь 
. Обратить двойные стрелки, вообще говоря, нельзя.
Неравенства Чебышева:
1) 
;
2) для неотрицательной целочисленной случайной величины с конечным математическим ожиданием неравенство (иногда называется неравенством Маркова) имеет вид: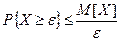 
.
Теорема Чебышева ( 
– последовательность независимых случайных величин, имеющих дисперсии, ограниченные одной и той же постоянной):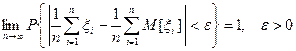 
.
|
|
|
