 |
Задачи с решениями
|
|
|
|
1. Случайная величина X задана плотностью распределения вероятностей: 
. Найти производящую функцию начальных моментов.
Решение. По определению производящая функция начальных моментов определяется по формуле: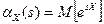 
. Используя свойство математического ожидания для функции от случайной величины, находим:
Введя подстановку 
, сведем интеграл к табличному и получим производящую функцию начальных моментов заданной случайной величины:
.
2. Найти производящую функцию начальных моментов и начальные моменты двух первых порядков случайной величины X, имеющей распределение: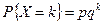 
; 
; 
.
Решение. Воспользовавшись определением производящей функции начальных моментов, свойством математического ожидания для функции от случайной величины и зная предел суммы членов бесконечно убывающей геометрической прогрессии, имеем:
.
Известно, что если задана производящая функция начальных моментов некоторой случайной величины, то начальные моменты этой величины можно найти по формуле: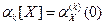 
. Применив эту формулу для нашего случая, получим начальные моменты двух первых порядков заданной случайной величины:
;
.
3. Пусть случайная величина X имеет производящую функцию начальных моментов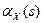 
. Найти производящие функции начальных моментов величин Y=aX+b и Z=-bX, когда a=3, b=2.
Решение. Найдем производящую функцию начальных моментов линейного преобразования Y=aX+b, воспользовавшись ее определением в форме математического ожидания:
Подставив вместо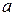 
и 
соответствующие значения, окончательно получим: 
; 
.
4. Найти производящую функцию центральных моментов случайной величины X, заданной рядом распределения
| X | ||||
| P | 0, 4 | 0, 3 | 0, 2 | 0, 1 |
Решение. Согласно определения, производящая функция центральных моментов случайной величины X находится по формуле: 
, которую легко свести к следующему виду:
|
|
|
. (*)
Найдем математическое ожидание 
и производящую функцию вероятностей 
.
;
.
Тогда производящая функция центральных моментов заданной случайной величины будет иметь следующий вид:
.
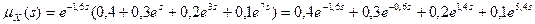5. Найти производящую функцию центральных моментов и центральные моменты двух первых порядков случайной величины X, заданной плотностью распределения вероятностей
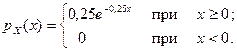
Решение. Для нахождения производящей функции центральных моментов воспользуемся формулой (*), полученной в задаче 4: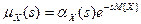 
. Определим математическое ожидание и производящую функцию начальных моментов:
;
.
Отсюда имеем: 
×
Зная производящую функцию центральных моментов, найдем центральные моменты двух первых порядков по формуле: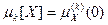 
. Следовательно,
;
.
6. Найти производящую функцию центральных моментов величины Z=X+Y, если известно, что случайные величины X и Y независимы, X имеет производящую функцию центральных моментов
,
а Y задана рядом распределения
| Y | ||
| P | 0, 1 | 0, 9 |
Решение. Для решения задачи воспользуемся свойством производящих функций центральных моментов для независимых случайных величин: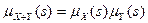 
. Найдем 
, используя формулу (*), полученную в задаче 4: 
, и зная, что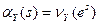 
. Тогда
;
;
.
Перемножив производящие функции центральных моментов величин X и Y и выполнив простейшие преобразования, получим
.
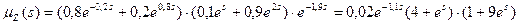7. Случайная величина X задана производящей функцией вероятностей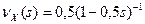 
. Найти производящую функцию факториальных моментов и математическое ожидание величины X.
Решение. Известно, что 
. Отсюда имеем:
.
Для нахождения математического ожидания воспользуемся известными соотношениями: 
, а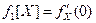 
. Следовательно,
.
8. Случайная величина X (число частиц, достигающих счетчика в некотором физическом опыте с радиоактивными частицами) распределена по следующему эмпирическому закону, заданному таблицей:
|
|
|
| X | |||||||||||
| P | 0, 021 | 0, 081 | 0, 156 | 0, 201 | 0, 195 | 0, 151 | 0, 097 | 0, 054 | 0, 026 | 0, 011 | 0, 007 |
Найти факториальные моменты двух первых порядков.
Решение. Для нахождения производящей функции факториальных моментов заданной величины X воспользуемся соотношением: . Отсюда
Зная производящую функцию факториальных моментов, найдем факториальные моменты заданной случайной величины по формуле: 
.
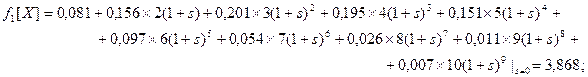
9. Найти производящую функцию факториальных моментов и факториальные моменты случайной величины X, заданной распределением Бернулли: 
; ; 
.
Решение. По определению производящая функция факториальных моментов есть 
. Применив эту формулу для нашего случая, имеем
.
Найдем факториальные моменты бернуллиевской случайной величины по формуле: .
; 
, 
.
10. Законы распределения вероятностей независимых случайных величин X, Y и Z заданы таблично:
| X | ||
| P | 0, 7 | 0, 3 |
| Y | ||
| P | 0, 5 | 0, 5 |
| Z | ||
| P | 0, 2 | 0, 8 |
Найти производящую функцию факториальных моментов величины Q=X+Y+Z и математическое ожидание величины Q.
Решение. Известно, что для независимых случайных величин 
. Применив соотношение, связывающее производящую функцию факториальных моментов и производящую функцию вероятностей, получим:
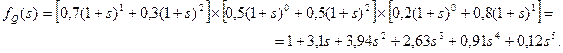
Зная, что 
, найдем математическое ожидание величины Q.
.
|
|
|
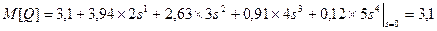