 |
Задачи для самостоятельной работы
|
|
|
|
Задачи для самостоятельной работы
10. 1. Найти закон распределения, которому соответствует производящая функция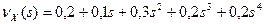 
.
10. 2. Найти производящую функцию вероятностей случайной величины Y, имеющей распределение Пуассона с параметром 
.
10. 3. Дискретная случайная величина X задана таблично:
| X | ||||
| P | 0, 5 | 0, 1 | 0, 3 | 0, 1 |
Найти производящую функцию вероятностей и математическое ожидание величины X.
10. 4. Законы распределения вероятностей независимых случайных величин X и Y заданы таблично:
| X | ||
| P | 0, 2 | 0, 8 |
| Y | ||
| P | 0, 6 | 0, 4 |
Найти производящие функции вероятностей X и Y и закон распределения величины Z=X+Y.
10. 5. Вывести производящую функцию вероятностей суммы независимых случайных величин X и Y, имеющих геометрическое распределение с параметром p.
10. 6. Неотрицательная целочисленная случайная величина X задана таблично:
| X | ||||
| P | 0, 4 | 0, 3 | 0, 2 | 0, 1 |
Найти производящую функцию вероятностей и факториальные моменты случайной величины X.
10. 7 Законы распределения вероятностей независимых случайных величин Y и Z заданы таблично:
| Y | ||
| P | 0, 1 | 0, 9 |
| Z | ||
| P | 0, 2 | 0, 8 |
Найти производящие функции вероятностей Y и Z и дисперсию величины X=Y+Z.
10. 8. Найти производящую функцию вероятностей суммы трех независимых случайных величин, имеющих бернуллиевское распределение с параметром p, математическое ожидание и дисперсию новой случайной величины.
10. 9. Найти законы распределения, которым соответствуют следующие производящие функции: 
, 
.
10. 10. Пусть X неотрицательная целочисленная случайная величина с производящей функцией 
. Найти производящие функции величин Y=X+1 и Z=2X.
|
|
|
10. 11. Найти производящую функцию вероятностей и факториальные моменты случайной величины, подчиняющейся закону распределения Паскаля с параметрами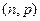 
.
10. 12. Найти производящую функцию вероятностей и дисперсию суммы трех независимых случайных величин, имеющих биномиальное распределение с параметрам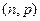и , 
и 
соответственно.
10. 13. Можно ли считать производящей функцией вероятностей функцию: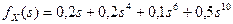 
?
10. 14. Случайная величина X задана производящей функцией 
. Найти закон распределения вероятностей (в виде таблицы), математическое ожидание и дисперсию величины X.
10. 15. Найти факториальные моменты случайной величины X, заданной производящей функцией вероятностей:
.
10. 16. Назовем циклом последовательность испытаний Бернулли до первой неудачи включительно. Найти производящую функцию и распределение вероятностей общего числа успехов в n циклах.
10. 17. При каких значениях параметров дробно-линейная функция 
является производящей функцией вероятностей?
10. 18. Независимые случайные величины X и Y заданы производящими функциями: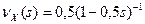 
, 
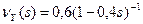. Найти производящую функцию вероятностей величины 
.
10. 19. Независимые случайные величины Y и Z заданы производящими функциями: 
, 
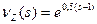. Найти математическое ожидание величины 
.
10. 20. Может ли функция 
быть производящей функций вероятностей? Если да, то найти распределение вероятностей, которому она соответствует.
10. 21. Случайные величины X и Y заданы таблично.
| X | ||
| P | 0, 5 | 0, 5 |
| X | ||||
| P | 0, 125 | 0, 25 | 0, 5 | 0, 125 |
Доказать, что не существует случайной величины Z, не зависящей от X и такой, что X+Z=Y.
11. ПРОИЗВОДЯЩИЕ ФУНКЦИИ МОМЕНТОВ
Основные понятия раздела
Бесконечный ряд однотипных моментов (если такой существует) предполагает существование соответствующей производящей функции точно так же, как это было с рядом вероятностей. Для НЦСВ таким требованиям удовлетворяет функция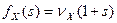 
, называемая производящей функцией факториальных моментов (ПФФМ), ипозволяющая находить факториальные моменты: 
. В терминах математических ожиданий 
.
|
|
|
По распределению вероятностей случайной величины X определяются также производящая функция начальных моментов (ПФНМ) 
и производящая функция центральных моментов (ПФЦМ) 
. Аргумент s – любое комплексное число, для которого приведенные интегралы (суммы) сходятся абсолютно.
Если для распределения вероятностей случайной величины X существует начальный момент соответствующего порядка, то его можно найти по формуле: 
. Аналогично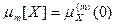 
.
Производящие функции моментов (ПФНМ, ПФЦМ и ПФФМ) обладают рядом общих и важных в прикладном аспекте свойств. Главное из них может быть сформулировано следующим образом: производящая функция моментов суммы X независимых случайных величин X1,..., Xn равна произведению соответствующих производящих функций слагаемых, т. е. 
. Здесь в качестве функций j могут фигурировать ПФФМ, ПФНМ или ПФЦМ.
|
|
|
