Задачи для самостоятельной работы

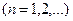13. 1. Дана последовательность независимых случайных величин . Случайная величина  может принимать только три значения:  с вероятностями, равными соответственно . Применима ли к данной последовательности теорема Чебышева?

13. 2. Последовательность независимых случайных величин  задана законом распределения:

	a	-a
P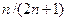

Применима ли к исходной последовательности теорема Чебышева?

13. 3. Доказать, что из сходимости в среднем любого порядка следует сходимость по вероятности.

13. 4. Используя неравенство Чебышева, найти вероятность того, что относительная частота появления герба при ста бросаниях монеты отклонится от вероятности не более чем на 0, 1.

13. 5. Производится большое число n независимых опытов, в каждом из которых случайная величина X имеет равномерное распределение на участке [0, 2]. На основе закона больших чисел выяснить, к какому числу a будет приближаться (сходиться по вероятности) при  величина . Оценить ошибку равенства .

13. 6. Случайные величины  распределены равномерно на участках [-1, 1], [-2, 2], …, [-n, n]. Будет ли среднее арифметическое этих величин при увеличении n сходиться по вероятности к 0.

13. 7. Длина изготовляемых изделий представляет случайную величину, математическое ожидание которой равно 90 см. Дисперсия этой величины равна 0, 0225. Используя неравенство Чебышева, оценить вероятность того, что: а) отклонение длины изготовленного изделия от ее математического ожидания по абсолютной величине не превзойдет 0, 4; б) длина изделия выразится числом, заключенным между 89, 7 и 90, 3 см.

13. 8. Вычислительная машина вырабатывает двоичные числа так, что знаки 0 и 1 на каждой позиции появляются с одинаковой вероятностью и независимо от других позиций. Последовательность знаков делится на группы, состоящие из одинаковых знаков, например, 000 111 0 1 00 1111 00 11 0000 1 0... . Подсчитывается число знаков в каждой группе и делится на число групп. Как будет вести себя средняя величина при неограниченном увеличении числа групп n?

13. 9. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за время t равна 0, 05. Оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и математическим ожиданием отказов за время t окажется меньше двух.

13. 10. В очереди на получение денег в кассу стоит n=60 человек; размер выплаты каждому из них случаен. Средняя выплата M[X]=50 у. е. , среднеквадратическое отклонение выплаты σ [X]=20 у. е. Выплаты отдельным получателям независимы. Сколько должно быть денег в кассе, чтобы их с вероятностью 0, 95 хватило на выплату всем 60 получателям? Каков будет гарантированный с той же вероятностью 0, 95 остаток денег b в кассе после выплаты всем 60 получателям, если в начале выплаты в кассе было 3500 у. е.?

13. 11. Вероятность появления события A в одном опыте равна 0, 5. Можно ли с вероятностью, большей 0, 97, утверждать, что число появлений события A в 1000 независимых опытах будет в пределах от 400 до 600?

13. 12. Определить, имеет ли место закон больших чисел для среднего арифметического из n попарно независимых случайных величин 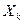, заданных рядом распределения

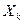
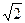
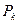
	0, 25	0, 5	0, 25

13. 13. Доказать, что к среднему арифметическому последовательности независимых случайных величин 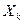, заданных рядом распределения

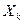
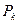
	0, 5	0, 5

применим закон больших чисел.

13. 14. Дискретная случайная величина X задана законом распределения

Оценить вероятность того, что .

13. 15. Задана последовательность  – независимых одинаково распределенных случайных величин с плотностью ; Y – положительная, не зависящая от них целочисленная случайная величина с законом распределения . Найти закон распределения и числовые характеристики случайной величины .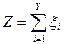

13. 16. Среднее значение скорости ветра у земли в данном пункте равно 16 км/ч. Оценить с помощью неравенства Чебышева вероятность того, что в этом пункте скорость ветра (при одном наблюдении) не превысит 80 км/ч.

13. 17. Известно, что при контроле бракуется 10% шестерен. Для контроля отобрано 500 деталей. Найти вероятность того, что число годных шестерен окажется в пределах от 460 до 475.

13. 18. Математическое ожидание количества выпадающих в течение года в данной местности осадков составляет 55 см. Оценить вероятность того, что в этой местности осадков выпадет 175 см.

13. 19. Число солнечных дней в году для данной местности является случайной величиной с математическим ожиданием, равным 75 дням. Оценить вероятность того, что в течение года в этой местности будет не более 200 солнечных дней.

13. 20. Дисперсия каждой из 2500 независимых случайных величин не превосходит 5. Оценить вероятность того, что отклонение среднего арифметического этих случайных величин от их математических ожиданий не превзойдет 0, 4.

13. 21. Дана последовательность независимых случайных величин 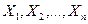; ; . Применим ли к этой последовательности закон больших чисел?