 |
10. Производящая функция вероятностей
|
|
|
|
10. ПРОИЗВОДЯЩАЯ ФУНКЦИЯ ВЕРОЯТНОСТЕЙ
Основные понятия, теоремы и следствия раздела
Среди дискретных случайных величин особое место занимают величины, принимающие только целые неотрицательные значения (0, 1, 2, …). Такие случайные величины называются неотрицательными целочисленными (НЦСВ).
Сумма степенного ряда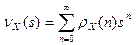 
называется производящей функцией вероятностей (ПФВ) 
. ПФВ является аналитической функцией аргумента при ½ s½ < 1, и приведенная формула дает ее разложение в степенной ряд. Это определение может быть записано в виде математического ожидания 
.
Теорема 1. Распределение вероятностей 
НЦСВ X однозначно определяется соответствующей ПФВ посредством формулы
.
Теорема 2. Если факториальный момент n-го порядка НЦСВ X существует, то 
.
Следствие 1. Для математического ожидания M[X] НЦСВ X (если оно существует) справедливо выражение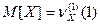 
.
Следствие 2. Для дисперсии D[X] НЦСВ X справедливо выражение
,
если эта дисперсия существует (т. е. D[X] < ¥ ).
Теорема 3. Если X=X1+... +Xn, и слагаемые в этой сумме представляют собой независимые НЦСВ, то 
.
В частности, если величины X1,..., Xn одинаково распределены и имеют ПФВ n(s), то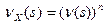 
.
Теорема 4. Сумма Y = X1 +... + XN случайного числа независимых и одинаково распределенных НЦСВ имеет ПФВ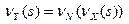 
, где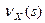 
– ПФВ слагаемых, 
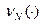– ПФВ числа слагаемых.
Теорема 5. ПФВ случайной величины Y = mX + n, где т, п ‑ неотрицательные целые числа, а X – НЦСВ, имеет вид: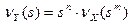 
.
Основные свойства ПФВ.
П1. Функция n(s), определенная на замкнутом интервале от 0 до 1, является производящей функцией вероятностей некоторой случайной величины, если 
, где a0+a1+a2+... =1, an ³ 0.
П2. ПФВ монотонно возрастает при s®1 от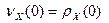 
до 
. Последнее равенство имеет место, если 
.
|
|
|
Задачи с решениями
1. Пусть p – вероятность " успеха" в независимых испытаниях Бернулли, а X – число " неудач", предшествующих первому " успеху". Найти производящую функцию вероятностей величины X.
Решение. Для нахождения производящей функции вероятностей воспользуемся ее определением вида: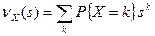 
. Согласно условий задачи величина X имеет геометрическое распределение:
, 
, 
.
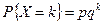Отсюда получаем
.
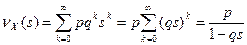2. Найти распределение, которому соответствует производящая функция вероятностей 
.
Решение. Для нахождения распределения величины X воспользуемся свойством функции 
производить вероятности, с которыми неотрицательная целочисленная случайная величина принимает свои значения:
.
Найдем последовательно производные производящей функции и вычислим их значения в точке 0:
; 
;
; 
при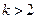 
.
Таким образом, заданная производящая функция вероятностей соответствует биномиальному распределению с параметрами p=0, 5 и n=2.
3. Пусть неотрицательная целочисленная случайная величина X имеет производящую функцию . Найти производящие функции величин 
и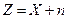 
(n – целое неотрицательное число).
Решение. Для нахождения производящих функций величин Y и Z применим определение: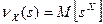 
. Подставляя выражения для Y и Z в эту формулу и используя свойства математического ожидания, получим:
.
.
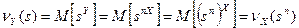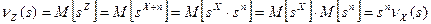4. Законы распределения вероятностей независимых случайных величин X, Y и Z заданы таблично:
| X | ||
| P | 0, 7 | 0, 3 |
| Y | ||
| P | 0, 5 | 0, 5 |
| Z | ||
| P | 0, 2 | 0, 8 |
Найти производящую функцию и распределение (в форме таблицы) для величины Q=X+Y+Z.
Решение. Для нахождения распределения величины Q, определим ее производящую функцию, и по ней построим таблицу. Известно, что производящая функция вероятностей суммы независимых неотрицательных целочисленных случайных величин равняется произведению производящих функций слагаемых. По определению вида 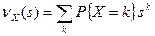имеем: 
; 
; 
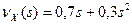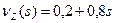. Отсюда
|
|
|
Распределение в форме таблицы имеет вид:
| X | |||||
| P | 0, 07 | 0, 31 | 0, 19 | 0, 31 | 0, 12 |
Условие нормировки выполняется: 
.
5. Пусть X – неотрицательная целочисленная случайная величина с производящей функцией . Найти 
.
Решение. Зная производящую функцию вероятностей, математическое ожидание величины X можно найти по формуле: 
. Введем обозначение: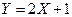 
, и на основании свойств производящей функции (см. задачу 3) найдем 
. Отсюда
.
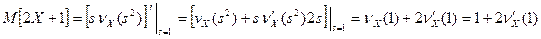6. Неотрицательная целочисленная случайная величина X задана производящей функцией 
. Найти дисперсию величины X.
Решение. Для дисперсии неотрицательной целочисленной случайной величины 
справедливо выражение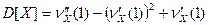 
. Используя эту формулу, находим 
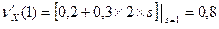и 
. Тогда
.
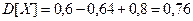7. Найти производящую функцию числа X успехов в n независимых испытаниях Бернулли, если вероятность успеха в каждом испытании равна p.
Решение. Согласно условиям задачи случайная величина X представляет собой сумму независимых бернуллиевских величин 
, что соответствует определению величины, имеющей биномиальное распределение. Известно, что если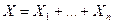 
, и слагаемые в этой сумме независимые неотрицательные целочисленные случайные величины, то 
. Найдем производящие функции величин 
: 
, и окончательно получим
.
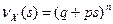8. Покажите, что функция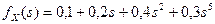 
может быть производящей функцией вероятностей случайной величины X.
Решение. Любая степенная функция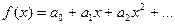 
может быть признана производящей функцией вероятностей, если она отвечает следующим свойствам:
1) коэффициенты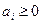 
, и их сумма равна 1;
2) функция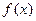 
монотонно возрастает при 
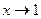от 
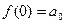до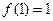 
.
Функция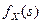 
является степенной, проверим выполнение необходимых условий:
1) коэффициенты при степенях s положительны, а их сумма равняется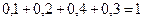 
;
2) при 
функция возрастает от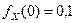 
до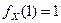 
.
Таким образом, заданная функция 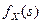может быть производящей функцией вероятностей величины X.
9. Независимые случайные величины X и Y заданы производящими функциям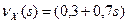и 
, и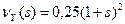 
соответственно. Найти распределение величины Z=X+Y.
Решение. Согласно свойства производящей функции распределения вероятностей для независимых случайных величин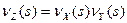 
. Отсюда получаем, что 
. Используя свойство функции производить вероятности, находим
|
|
|
;
;
;
.
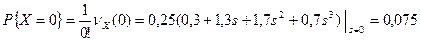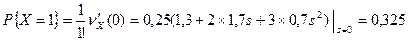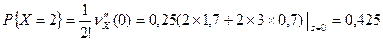Условие нормировки выполняется: 
.
10. Случайная величина X задана производящей функцией вероятностей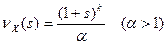 
. Найти факториальные моменты величины X.
Решение. Производящая функция вероятностей позволяет находить факториальные моменты неотрицательной целочисленной случайной величины X по формуле: 
. Применим эту формулу для нашей задачи:
;
;
;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
|
|
|
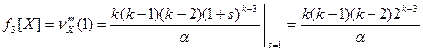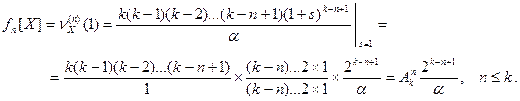
