 |
12. Характеристическая функция и другие линейные преобразования
|
|
|
|
12. ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ И ДРУГИЕ ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
Основные понятия раздела
Характеристической функцией (ХФ) случайной величины X с функцией распределения FX(× ) называется комплекснозначная функция, задаваемая формулой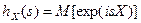 
или, что эквивалентно, формулой 
.
В частности, если существует плотность распределения вероятностей, то ХФ есть преобразование Фурье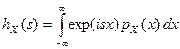 
плотности распределения pX(× ) с обратным преобразованием 
, если ХФ суммируема на вещественной оси.
Основные свойства характеристических функций.
ХФ1. Для любой случайной величины X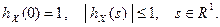 
ХФ2. Характеристическая функция равномерно непрерывна на числовой оси.
ХФ3. Характеристическая функция является положительно определенной.
ХФ4. Характеристическая функция является эрмитовой, т. е. имеет место равенство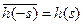 
.
ХФ5. Если Х1,..., Хn независимы, то 
.
ХФ6. Если Y = аX+b, где а и b – постоянные, то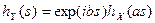 
.
ХФ7. Функция 
– четная, а 
– нечетная. Характеристическая функция действительна тогда и только тогда, когда соответствующее распределение симметрично: 1–FX (–t+0) = FX(t).
ХФ8. Если существует абсолютный момент 
, то существует п-я производная ХФ и 
.
Для достаточно малых значений аргумента s главная ветвь логарифмической функции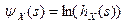 
называется y-функцией или производящей функцией семиинвариантов (ПФС).
Если существует п-й абсолютный момент, то в окрестности s = 0 ПФС непрерывно дифференцируема до порядка п включительно, причем, с учетом разложения ПФС в ряд Маклорена,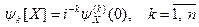 
. Эта величина называется семиинвариантом порядка k (кумулянтом порядка k).
При сложении независимых случайных величин Y = X1+... +Xn производящие функции семиинвариантов складываются: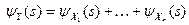 
, складываются также и семиинварианты одного порядка: 
.
|
|
|
Связь между семиинвариантами и моментами в общем виде громоздка. Исключение составляют моменты первых трех порядков:
Отношения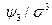 
и 
получили название коэффициентов асимметрии и эксцесса.
Преобразованием Лапласа (односторонним) функции распределения вероятностей FX(t) (или случайной величины Х) называется функция
,
определенная для t ³ 0, Re(s) ³ 0 и аналитическая при Re(s) > 0 (Re(s) = l, если s = l+in).
Если плотность распределения вероятностей pX(t) непрерывна, то 
, где интеграл понимается в смысле главного значения.
Преобразование Лапласа представляется в виде математического ожидания и в виде ряда
в круге 0 £ s < s0, в котором последний ряд сходится.
Основные свойства преобразования Лапласа.
ПЛ1. Если Х1,..., Хn – неотрицательные и независимые случайные величины, то их сумма Y имеет преобразование Лапласа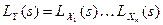 
.
ПЛ2. Если Y = аX+ b, причем а, b, X ³ 0, то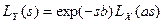 
.
ПЛ3. Если k-й начальный момент существует, то 
.
Задачи с решениями
1. Случайная величина X равномерно распределена на отрезке [0, 2]. Найти характеристическую функцию этой величины.
Решение. Известно, что если для некоторой случайной величины X существует плотность распределения вероятностей 
, то характеристическая функция этой величины может быть найдена как преобразование Фурье 
. Для нашего случая имеем:
тогда 
.
2. Случайная величина X задана плотностью распределения вероятностей:
Найти характеристическую функцию и начальные моменты двух первых порядков величины X.
Решение. Применив преобразование Фурье к заданным условиям, получим
.
Введя подстановку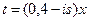 
, найдем выражение для характеристической функции заданной случайной величины
.
Зная характеристическую функцию, найдем начальные моменты двух первых порядков по формуле: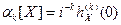 
.
;
.
3. Независимые случайные величины X и Y имеют характеристические функции 
и 
соответственно. Найти характеристическую функцию величины Q=U+V, если U=2X+3 и V=-Y.
|
|
|
Решение. Используя определение 
и свойство характеристической функции для независимых случайных величин 
, находим
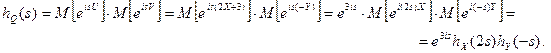
4. Найти плотность распределения вероятностей, которой соответствует характеристическая функция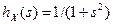 
.
Решение. Плотность распределения связана с характеристической функцией обратным преобразованием Фурье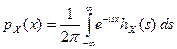 
. Применим его для нашего случая 
.
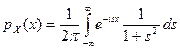Будем рассматривать s как вещественную часть комплексной переменной 
. При 
интеграл по вещественной оси равен интегралу по замкнутому контуру, состоящему из вещественной оси и полуокружности бесконечно большого радиуса, лежащей в верхней полуплоскости (рис. 12. 1), т. е. 
. На основании теоремы о
 |
вычетах
. Отсюда, учитывая, что , имеем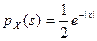 
.
Аналогичным образом при 
плотность 
, где интегрирование ведется по тому же контуру (рис. 12. 1), и на основании теоремы о вычетах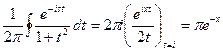 
, а также учитывая, что , имеем 
.
Таким образом, случайная величина X имеет распределение Лапласа с параметрами (0, 1).
5. Случайная величина X задана плотностью распределения вероятностей 
на всей действительной оси. Найти производящую функцию семиинвариантов.
Решение. Для нахождения производящей функции семиинвариантов воспользуемся ее определением, задаваемым формулой 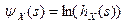. Найдем характеристическую функцию заданной случайной величины, используя для вычисления интеграла рассуждения, приведенные в предыдущем примере.
.
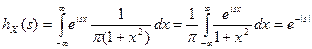Тогда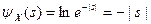 
.
6. Случайная величина X имеет характеристическую функцию 
. Найти производящую функцию семиинвариантов, математическое ожидание, дисперсию, асимметрию и эксцесс величины X.
Решение. По определению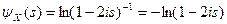 
. Для нахождения требуемых числовых характеристик воспользуемся свойством производящей функции семиинвариантов: 
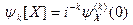, и формулами связи кумулянтов и заданных числовых характеристик:
; 
; 
; 
.
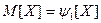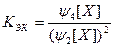Отсюда имеем
;
;
;
;
; 
.
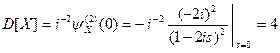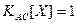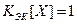7. Независимые случайные величины X, Y и Z заданы производящими функциями семиинвариантов: 
. Найти математическое ожидание и дисперсию величины Q=X+Y+Z.
Решение. Зная свойство производящей функции кумулянтов для независимых случайных величин 
, получим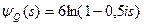 
. Отсюда находим математическое ожидание и дисперсию величины Q.
|
|
|
;
.
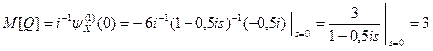8. Вывести двухстороннее преобразование Лапласа для случайной величины X, имеющей стандартное нормальное распределение.
Решение. Двухстороннее преобразование Лапласа в общем случае имеет вид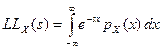 
. Подставив в эту формулу плотность стандартного нормального распределения, находим
.
9. Найти односторонее (правостороннее) преобразование Лапласа величины Z=X+Y, если известно, что X и Y независимы и имеют следующие производящие функции начальных моментов: 
, 
.
Решение. Известно, что одностороннее (правостороннее) преобразование Лапласа связано с производящей функцией начальных моментов соотношением 
. Зная свойство преобразования Лапласа для независимых случайных величин, имеем
.
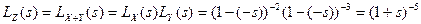10. Случайная величина X задана односторонним (правосторонним) преобразованием Лапласа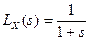 
. Найти математическое ожидание и дисперсию величины X.
Решение. По свойству преобразования Лапласа 
находим
;
.
|
|
|
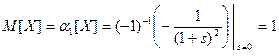