 |
Задачи с решениями
|
|
|
|
1. (Правило " трех сигм". ) Используя неравенство Чебышева, оценить сверху вероятность того, что случайная величина X, имеющая математическое ожидание a и среднеквадратическое отклонение σ , отклонится от a менее чем на 3σ .
Решение. Неравенство Чебышева дает
.
Отсюда имеем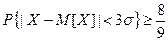 
. Итак, любая случайная величина отходит от своего математического ожидания меньше, чем на 3σ , с вероятностью, не меньшей, чем 8/9.
Примечание. Это – крайний, самый неблагоприятный случай. На практике для обычно встречающихся случайных величин эта вероятность гораздо ближе к единице. Например, для нормального закона она равна 0, 997; для равномерного распределения – единице; для показательного – 0, 982.
2. Задана последовательность случайных величин 
, имеющих равномерное распределение соответственно на участках [0, 1], [0, 2], … [0, n]. Будет ли иметь место сходимость этой последовательности к случайной величине X в среднем порядка r=1?
Решение. Последовательность случайных величин называется сходящейся в среднем порядка r к случайной величине ξ , если
.
В силу определения случайные величины 
, 
и 
. Тогда для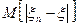 
возможны два случая:
1) если 
, то 
, тогда
2) если 
, то 
, тогда
Следовательно, если 
конечная величина, то сходимость последовательности в среднем порядка r=1 отсутствует.
3. Цех завода выпускает шарики для подшипников. За смену производится n=100000 шариков. Вероятность того, что один шарик окажется дефектным, равна 0, 05. Причины дефектов для отдельных шариков независимы. Продукция проходит контроль сразу после изготовления, причем дефектные шарики бракуются и ссыпаются в бункер, а небракованные отправляются в цех сборки. Определить, на какое количество шариков должен быть рассчитан бункер, чтобы с вероятностью 0, 99 после смены он не оказался переполненным.
|
|
|
Решение. Число X бракованных шариков имеет биномиальное распределение. Так как n достаточно велико, то на основании центральной предельной теоремы распределение X можно считать приблизительно нормальным с математическим ожиданием 
и дисперсией 
.
Найдем такое значение x, для которого 
. Для этого воспользуемся таблицей функции распределения стандартной нормальной величины (таблицей функции Лапласа), т. е. 
. Тогда 
и 
. Таким образом, бункер, рассчитанный примерно на 550 шариков, с вероятностью 0, 99 за смену переполняться не будет.
4. Независимые случайные величины 
, 
, ... распределены одинаково по показательному закону с параметром 
. Найти закон распределения и числовые характеристики случайной величины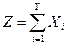 
, где случайная величина Y имеет геометрическое распределение с параметром p, начинающееся с 1.
Решение. Известно, что сумма фиксированного числа n независимых случайных величин 
с одинаковым показательным распределением подчинена закону Эрланга с плотностью распределения с параметрами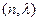 
: 
.
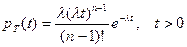Плотность случайной величины Z легко находится по формуле полной вероятности с гипотезами 
:
Таким образом, случайная величина Z также будет подчинена показательному закону распределения, но с параметром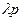 
. Отсюда числовые характеристики: 
, 
.
5. Из 1000 изделий, отправляемых в сборочный цех, было подвергнуто обследованию 200, отобранных случайным образом. Среди них оказалось 25 бракованных. Приняв долю бракованных изделий среди отобранных за вероятность изготовления бракованного изделия, оценить вероятность того, что во всей партии бракованных изделий окажется не более 15% и не менее 10%.
Решение. Определим вероятность изготовления бракованного изделия: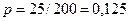 
.
Наибольшее отклонение частоты появлений бракованных изделий от вероятности p по абсолютной величине равно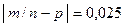 
. Используя неравенство Чебышева, находим
|
|
|
.
6. Средний расход воды в населенном пункте составляет 50000 л в день. Оценить вероятность того, что в этом населенном пункте в данный день расход воды не превысит 150000 л.
Решение. Применив для решения задачи неравенство Чебышева в форме 
, получим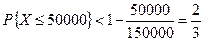 
.
7. Математическое ожидание скорости ветра на данной высоте равно 25 км/ч, а среднеквадратическое отклонение 4, 5 км/ч. Какие скорости ветра можно ожидать на этой высоте с вероятностью, не меньшей 0, 9?
Решение. Обозначив через X скорость ветра, запишем неравенство Чебышева 
. Отсюда 
км/ч и, следовательно, с вероятностью, большей 0, 9, имеем 
.
8. Среднеквадратическое отклонение ошибки измерения азимута равно 30', а математическое ожидание равно нулю. Оценить вероятность того, что ошибка среднего арифметического трех независимых измерений не превзойдет 1°.
Решение. Пусть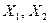 
и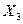 
– ошибки трех наблюдений, тогда ошибка среднего арифметического этих наблюдений 
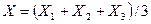имеет дисперсию 
.
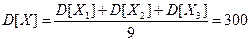Оценим искомую вероятность, используя неравенство Чебышева
.
9. Случайная величина X имеет математическое ожидание M[X]=1 и среднеквадратическое отклонение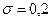 
. С помощью неравенства Чебышева оценить вероятность неравенства 
.
Решение. Перепишем заданное неравенство, прибавив к каждой его части -1: 
или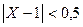 
. Оценим искомую вероятность, используя неравенство Чебышева 
.
10. Дана последовательность независимых случайных величин 
, распределенных по нормальному закону с параметрами 
. Найти предельный закон распределения суммы этих величин при 
, если ряд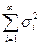 
сходится.
Решение. Введем обозначения: 
и 
. Известно, что характеристическая функция нормально распределенной случайной величины имеет вид: 
и 
. Отсюда имеем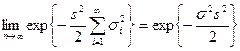 
.
|
|
|
