 |
Средние скорости молекул идеального газа. 1 глава
|
|
|
|
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
Тульский государственный университет
И.Ю. Канунникова
Механика. Термодинамика. Молекулярная физика.
Методические указания
и контрольные задания
Учебное пособие
Тула 2007
УДК 537(07)
Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей. Учеб. пособие/ И.Ю. Канунникова. Тула: Изд-во ТулГУ, 2007 – 102 с
В пособии изложена рабочая программа курса физики по разделам: «Механика. Физические основы классической механики. Элементы специальной теории относительности» и «Молекулярная физика и термодинамика». Приведены краткие теоретические сведения по каждому разделу, примеры решения задач, контрольные задания, правила оформления контрольных работ, сведения о приближенных вычислениях, таблицы интегралов и дифференциалов, основы векторной алгебры, справочные таблицы.
Предназначено для студентов-заочников инженерно-технических специальностей.
Табл. 9 Ил. 38. Библиогр.: 10 назв.
Печатается по решению библиотечно-издательского совета Тульского государственного университета
Рецензент: проф. кафедры физики ЕН факультета Тульского гос. университета, доктор физ.-мат. наук Д.М. Левин
© И.Ю. Канунникова, 2007
© Издательство ТулГУ, 2007
Рабочая программа курса физики
по механике, молекулярной физике и термодинамике
Введение
Предмет физики. Методы физического исследования: опыт, гипотеза, эксперимент, теория. Роль физики в развитии техники и влияние техники на развитие физики. Единицы физических величин.
|
|
|
Физические основы классической механики
Кинематика. Радиус-вектор. Траектория. Скорость. Ускорение. Криволинейное движение. Нормальное и тангенциальное ускорение. Вращательное движение. Угловая скорость и угловое ускорение. Связь угловых и линейных характеристик движения. Переход от неподвижной системы отсчета к движущейся.
Динамика материальной точки. Сила. Масса. Импульс. Фундаментальные взаимодействия. 1-й, 2-й и 3-й законы Ньютона. Преобразования Галилея. Классическая теорема сложения скоростей. Принцип относительности Галилея. Инерциальные и неинерциальные системы отсчета. Силы инерции и их примеры.
Система материальных точек. Полный импульс системы. Центр масс и его координаты. Уравнение движения центра масс. Закон сохранения и изменения полного импульса системы. Движение тела с переменной массой. Уравнение Мещерского.
Работа силы. Консервативные силы. Центральные силы (примеры). Потенциальная энергия. Связь потенциальной энергии и консервативных сил. Градиент. Эквипотенциальные поверхности. Потенциальная энергия системы материальных точек. Кинетическая энергия. Закон сохранения полной механической энергии. Неконсервативные силы. Диссипативные силы. Закон изменения механической энергии.
Потенциальное поле. Гравитационное поле. Закон тяготения Ньютона. Характеристики поля: напряженность и потенциал. Связь напряженности и потенциала гравитационного поля. Потенциальные кривые.
Момент силы. Момент импульса. Основное уравнение динамики вращательного движения. Вращение тела вокруг неподвижной оси. Момент импульса тела относительно оси. Момент сил относительно оси. Момент инерции материальной точки и физического тела. Вычисление моментов инерции. Теорема Штейнера. Основное уравнение вращательного движения тела вокруг закрепленной оси. Полный момент импульса системы и закон его сохранения и изменения. Работа момента силы. Кинетическая энергия вращающегося тела. Система центра масс. Плоское движение. Законы сохранения энергии и импульса в системе центра масс. Движение в поле центральных сил. Задача Кеплера.
|
|
|
Гармонические колебания. Осциллятор. Условие гармонических колебаний. Незатухающие гармонические колебания. Физический и математический маятники (примеры). Затухающие гармонические колебания. Кинематическое и динамическое уравнения затухающих гармонических колебаний. Механическая энергия осциллятора. Сложение гармонических колебаний: а) взаимно-перпендикулярных, б) однонаправленных. Метод векторной диаграммы. Вынужденные колебания. Динамическое уравнение вынужденных гармонических колебаний и его решение. Резонанс. Резонансная частота. Анализ периодических движений с помощью потенциальных кривых.
Элементы специальной теории относительности
Опыты Майкельсона-Морли и их результат. Постулаты СТО Эйнштейна. Принцип относительности Эйнштейна. Одновременность и синхронизация часов. Преобразования Лоренца и их следствия: релятивистское замедление времени и сокращение длины. Релятивистская теорема сложения скоростей. Релятивистский импульс и энергия частицы. Релятивистское уравнение динамики. Полная энергия и энергия покоя. Закон сохранения полной энергии. Связь энергии покоя и массы.
Четырехмерное пространство Минковского. Релятивистские инварианты. Интервал. Связь релятивистской энергии и импульса.
Молекулярная физика и термодинамика
Термодинамический и молекулярно-кинетический способы описания. Термодинамическая система. Равновесные и неравновесные, обратимые и необратимые процессы. Температура. Нулевое начало термодинамики. Уравнение состояния идеального газа. Работа идеального газа. Работа при циклических процессах. Внутренняя энергия термодинамической системы. Первое начало термодинамики. Внутренняя энергия и 1-е начало термодинамики для идеального газа. Теплоемкость. Теплоемкости идеального газа при постоянных объеме и давлении. Уравнение Майера. Адиабатический процесс и его уравнение для идеального газа. Политропический процесс.
|
|
|
Термодинамическое определение энтропии. Второе начало термодинамики. Невозможность существования вечных двигателей 1-го и 2-го рода. Формулировки Кельвина и Клаузиуса II-го начала термодинамики. Тепловые машины и циклические процессы. К.п.д. цикла. Цикл Карно и его к.п.д. Примеры тепловых машин (холодильник, кондиционер, тепловой насос).
Направление протекания естественных процессов. Микросостояние системы. Статистическое определение энтропии. Формула Больцмана для энтропии. III начало термодинамики (теорема Нернста).
Молекулярно-кинетическая теория газов. Функция распределения и ее смысл. Распределение Гаусса и его примеры. Распределение Максвелла для молекул идеального газа по проекциям скоростей. Распределение Максвелла для молекул идеального газа по величинам скоростей и его физический смысл. Экспериментальная проверка распределения Максвелла (опыты Штерна и Ламмерта). Средние скорости молекул газа. Температура в молекулярно-кинетической теории. Частота соударений молекул о стенку. Основное уравнение молекулярно-кинетической теории и его связь с уравнением состояния идеального газа. Теорема о равномерном распределении энергии по степеням свободы молекул. Внутренняя энергия и теплоемкость газа в молекулярно-кинетической теории. Идеальный газ в поле внешних сил. Барометрическая формула. Распределение Больцмана. Распределение Максвелла-Больцмана.
Необратимые процессы в газах. Столкновения молекул между собой. Эффективное сечение и средняя длина свободного пробега молекул газа. Явления переноса. Диффузия в газах. Теплопроводность газов. Вязкость газа. Реальный газ и уравнение его состояния (уравнение Ван-дер-Ваальса).
Литература.
1. Трофимова Т.И. Курс физики. – М.: Высш. шк., 1985.
2. Иродов И.Е. Основные законы механики. – М.: Высш. шк., 1986.
3. Колмаков Ю.Н., Пекар Ю.А., Лагун И.М., Лежнева Л.С. Механика и теория относительности. Лекции по физике. – Тул. гос. ун-т. Тула, 2002.
4. Колмаков Ю.Н., Пекар Ю.А., Лежнева Л.С. Термодинамика и молекулярная физика. Лекции по физике. – Тул. гос. ун-т. Тула, 1999.
|
|
|
5. Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Интеграл-Пресс, 1997. – 544с.
6. Трофимова Т.И., Павлова З.Г. Сб. задач по курсу физики с решениями: Учеб. пособие для вузов. – М.: Высш. шк., 1999. – 591с.
7. Фирганг Е.В. Руководство к решению задач по курсу общей физики. Учеб. пособие для втузов. – М.: Высш. шк., 1978.
Общие методические указания к выполнению контрольных работ.
1. В течение второго семестра студент-заочник выполняет две контрольные работы. Номера задач, которые студент должен включить в контрольную работу №1, определяются по таблице вариантов на стр. 45, в контрольную работу №2 – на стр. 92.
2. Контрольные работы нужно выполнять чернилами в школьной тетради в клетку; на обложке которой привести сведения по следующему образцу:
Контрольные работы №1 и №2
по физике
студента Иванова П.П.
группа 660151
3. Условия задач записать в сокращенном виде, перевести все данные в систему СИ. Каждую задачу следует писать с новой страницы. Для замечаний преподавателя на страницах тетради оставлять поля.
4. Выполненные контрольные работы студент представляет в деканат заочного факультета.
5. Если контрольная работа при рецензировании не зачтена, студент обязан представить ее на повторную рецензию, включив в нее те задачи, решения которых оказались неверными. Повторную работу необходимо представить вместе с незачтенной.
6. Зачтенные контрольные работы предъявляются экзаменатору. Студент во время экзамена должен быть готов дать пояснения по существу решения задач, входящих в его вариант контрольных задач.
7. Решения задач следует сопровождать краткими пояснениями; в тех случаях, когда это необходимо, рисунками, выполненными карандашом с использованием чертежных принадлежностей.
8. После получения расчетной формулы для проверки ее правильности следует подставить в правую часть формулы, вместо символов величин, обозначения единиц измерения этих величин и убедиться в том, что полученная в результате единица измерения соответствует искомой величине.
9. При подстановке в расчетную формулу, а также при записи ответа, числовые значения величин следует записывать как произведение десятичной дроби с одной значащей цифрой перед запятой на десять в соответствующей степени, округляя ответ до трех значащих цифр. Например, вместо 456297 надо записать 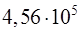 ; вместо 0,0004515 записать
; вместо 0,0004515 записать 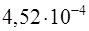 и т.п.
и т.п.
Контрольная работа №1
Кинематика. Динамика. Механические колебания
Основные формулы и примеры решения задач
1. Кинематика
В декартовой системе координат положение материальной точки описывается радиус-вектором (рис.1.1)
|
|
|
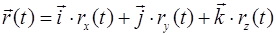 , (1.1)
, (1.1)
где 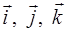 – орты, т.е. тройка взаимноперпендикулярных единичных
– орты, т.е. тройка взаимноперпендикулярных единичных  векторов, направленных вдоль координатных осей OX, OY, OZ.
векторов, направленных вдоль координатных осей OX, OY, OZ.
Кинематический закон движения:
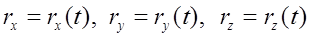 , (1.2)
, (1.2)
выражает зависимость координат точки от времени. С математической точки зрения они представляют собой уравнение траектории в параметрической форме, где роль параметра играет время.
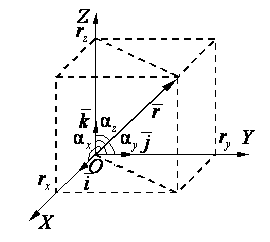
Рис. 1.1. Радиус-вектор  и его проекции
и его проекции 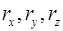 .
.
 – углы между радиус-вектором
– углы между радиус-вектором  и координатными осями OX, OY, OZ
и координатными осями OX, OY, OZ
Проекции радиус-вектора
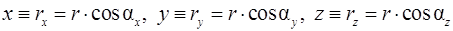 . (1.3)
. (1.3)
Модуль радиус-вектора
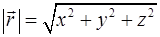 . (1.4)
. (1.4)
Путь, пройденный частицей за время 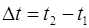 , равен длине траектории
, равен длине траектории 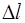 (рис.1.2). Вектор перемещения
(рис.1.2). Вектор перемещения 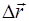 точки из положения 1 в положение 2:
точки из положения 1 в положение 2:
 . (1.5)
. (1.5)
Дифференцированием формул (1.2) можно найти проекции скорости и ускорения точки:
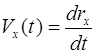 ,
, 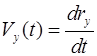 ,
, 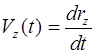 , (1.6)
, (1.6)
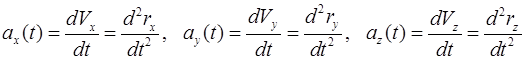 . (1.7)
. (1.7)
Мгновенная скорость: 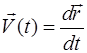 ,
,
 . (1.8)
. (1.8)
Средняя скорость:
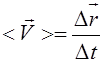 , (1.9)
, (1.9)
где 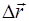 – перемещение материальной точки за время
– перемещение материальной точки за время  .
.
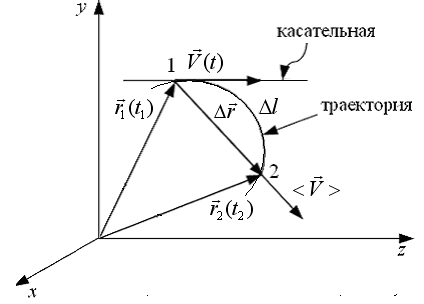
Рис. 1.2. Движение материальной точки из положения 1 в положение 2. 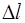 – путь, пройденный точкой.
– путь, пройденный точкой. 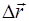 – вектор перемещения.
– вектор перемещения. 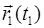 и
и 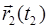 – радиус-векторы точки в моменты времени
– радиус-векторы точки в моменты времени 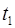 и
и 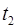 .
. 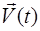 – мгновенная скорость точки.
– мгновенная скорость точки.  – средняя скорость точки
– средняя скорость точки
Модуль скорости 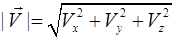 . (1.10)
. (1.10)
Модуль ускорения  . (1.11)
. (1.11)
Ускорение точки можно представить как сумму двух ускорений – тангенциального 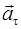 , т.е. касательного к траектории, и нормального
, т.е. касательного к траектории, и нормального 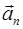 , т.е. перпендикулярного касательной к траектории в данной точке (рис.1.3):
, т.е. перпендикулярного касательной к траектории в данной точке (рис.1.3):
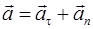 ,
, 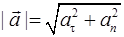 . (1.12)
. (1.12)
Тангенциальное ускорение обусловлено только изменением модуля скорости, а нормальное – только изменением направления скорости.
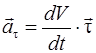 , (1.13)
, (1.13)
 , (1.14)
, (1.14)
где 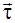 – единичный вектор, направленный вдоль касательной к траектории;
– единичный вектор, направленный вдоль касательной к траектории; 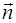 – единичный вектор, направленный к центру кривизны траектории (точка О); R – радиус кривизны траектории. Радиус-вектор
– единичный вектор, направленный к центру кривизны траектории (точка О); R – радиус кривизны траектории. Радиус-вектор  и перемещение измеряются в [м], скорость в [м/с], ускорение в [
и перемещение измеряются в [м], скорость в [м/с], ускорение в [ 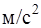 ].
].
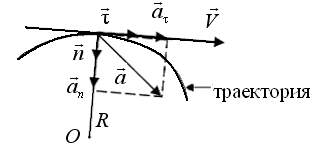
Рис. 1.3. Полное ускорение точки 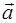 , представленное в виде векторной суммы тангенциального
, представленное в виде векторной суммы тангенциального 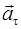 и нормального
и нормального 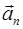 ускорений
ускорений
Кинематика движения точки по окружности
Твердое тело вращается вокруг неподвижной оси 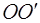 . Угол поворота тела характеризует вектор
. Угол поворота тела характеризует вектор 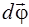 [*], модуль которого равен углу поворота, а направление совпадает с осью вращения
[*], модуль которого равен углу поворота, а направление совпадает с осью вращения 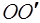 . Направление поворота отвечает правилу правого винта по отношению к направлению вектора
. Направление поворота отвечает правилу правого винта по отношению к направлению вектора 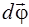 (рис. 1.4).
(рис. 1.4).
За бесконечно малый промежуток времени 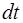 точка А тела, находящаяся на расстоянии R от оси вращения
точка А тела, находящаяся на расстоянии R от оси вращения 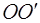 , повернется на угол
, повернется на угол 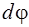 . Линейное перемещение точки А равно приращению радиус-вектора
. Линейное перемещение точки А равно приращению радиус-вектора 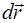 и связано с углом поворота
и связано с углом поворота 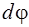 соотношением
соотношением
 . (1.15)
. (1.15)
В векторном виде 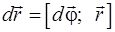 . (1.16)
. (1.16)
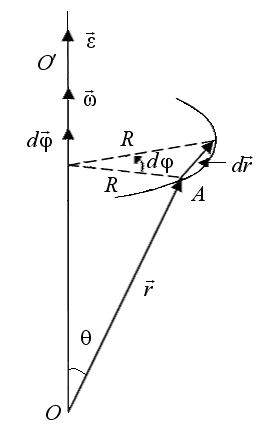
Рис.1.4. Вращение точки А вокруг неподвижной оси 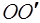 в горизонтальной плоскости.
в горизонтальной плоскости.
 – расстояние до оси вращения
– расстояние до оси вращения 
Вектор угловой скорости 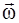 совпадает по направлению с вектором
совпадает по направлению с вектором 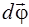 и представляет собой аксиальный вектор (греч. акси – ось)
и представляет собой аксиальный вектор (греч. акси – ось)
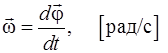 . (1.17)
. (1.17)
Угловое ускорение  . (1.18)
. (1.18)
Направление вектора 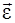 совпадает с направлением приращения вектора угловой скорости
совпадает с направлением приращения вектора угловой скорости 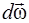 . Вектор
. Вектор 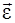 , как и
, как и 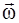 , является аксиальным.
, является аксиальным.
Связь между линейными и угловыми величинами
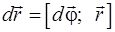 ,
, 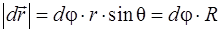 ,
,
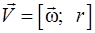 ,
, 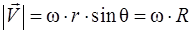 ,
,
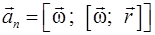 ,
, 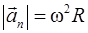 , (1.19)
, (1.19)
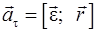 ,
,  .
.
Модуль полного ускорения
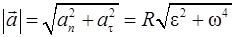 . (1.20)
. (1.20)
Обратная задача кинематики
Если известны зависимости  или
или 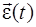 и начальные условия
и начальные условия 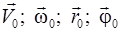 , то можно определить
, то можно определить
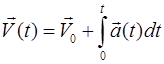 , (1.21)
, (1.21)
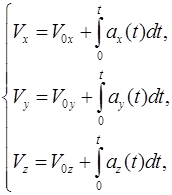 (1.22)
(1.22)
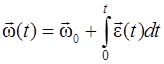 , (1.23)
, (1.23)
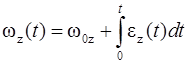 , (1.24)
, (1.24)
где 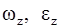 – проекции угловой скорости и углового ускорения на ось вращения.
– проекции угловой скорости и углового ускорения на ось вращения.
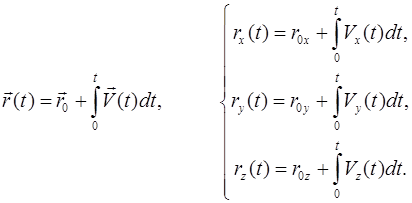 (1.25)
(1.25)
Путь, пройденный точкой за время t, 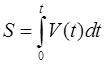 . (1.26)
. (1.26)
Угол поворота точки за время t 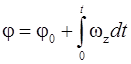 . (1.27)
. (1.27)
Примеры решения задач
Задача 1. Тело вращается вокруг неподвижной оси. Изменение угла поворота со временем определяется формулой 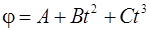 , где
, где 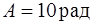 ,
, 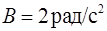 ,
, 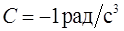 . Найти модуль полного ускорения точки, находящейся на расстоянии
. Найти модуль полного ускорения точки, находящейся на расстоянии 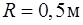 от оси вращения, для момента времени
от оси вращения, для момента времени 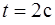 .
.
Решение. Модуль полного ускорения точки 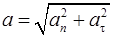 , (1)
, (1)
где 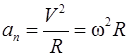 – нормальное ускорение,
– нормальное ускорение,  – тангенциальное ускорение.
– тангенциальное ускорение.
 . (2)
. (2)
Угловая скорость 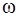 по определению равна производной от угла поворота по времени
по определению равна производной от угла поворота по времени 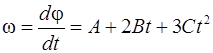 .
.
При 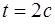
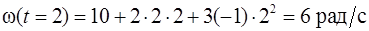 .
.
Угловое ускорение  равно производной от угловой скорости
равно производной от угловой скорости  по времени
по времени 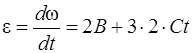 .
.
При 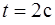
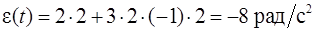 .
.
Знак минус показывает, что тело замедляет вращение с ускорением, зависимость которого от времени определяется выражением 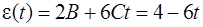 .
.
Подставив полученные значения 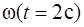 и
и 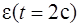 , а также значение
, а также значение 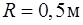 в формулу (2), получим
в формулу (2), получим
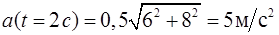 .
.
Задача 2. Частица начала движение из начала координат. Скорость ее зависит от времени по закону 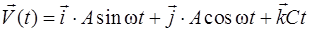 . Найти координаты частицы через
. Найти координаты частицы через  после начала движения, если
после начала движения, если 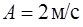 ,
, 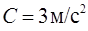 ,
, 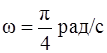 .
.
Решение. Проекции скорости частицы
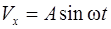 ,
,  ,
, 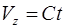 .
.
Проекции радиуса-вектора частицы (или координаты), в соответствии с формулами (1.24),
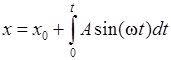 ;
; 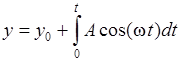 ;
; 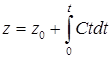 .
.
По условию частица начала движение из начала координат, т.е. 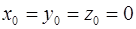 .
.
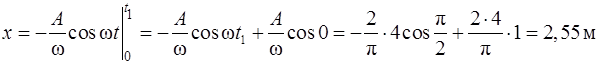 ,
,
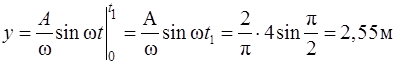 ,
,
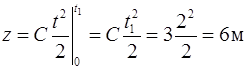 .
.
Координаты частицы  .
.
Задача 3. Частица начала двигаться из начала координат с начальной скоростью 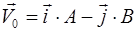 и с ускорением, которое зависит от времени по закону
и с ускорением, которое зависит от времени по закону 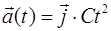 . Каков модуль скорости частицы в момент времени
. Каков модуль скорости частицы в момент времени 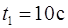 , если
, если 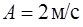 ,
, 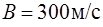 ,
,  ?
?
Решение. Проекции ускорения частицы
 ,
, 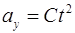 ,
, 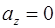 .
.
Проекции скорости 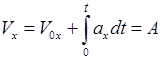 ,
,
 ,
,
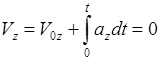 .
.
Модуль скорости частицы  ,
,
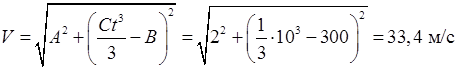 .
.
Задача 4. Частица начала двигаться из точки с радиус-вектором  со скоростью, которая зависит от времени по закону
со скоростью, которая зависит от времени по закону 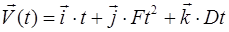 . На каком расстоянии от начала координат будет находится частица в момент времени
. На каком расстоянии от начала координат будет находится частица в момент времени 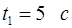 , если
, если 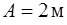 ,
, 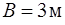 ,
, 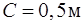 ,
, 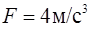 ,
, 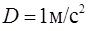 .
.
Решение. Проекции радиус-вектора частицы
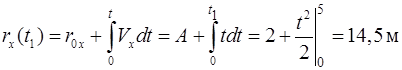 ,
,
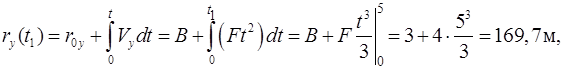
 .
.
Расстояние от начала координат до частицы в момент времени 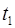 равно модулю радиус-вектора частицы при
равно модулю радиус-вектора частицы при 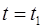
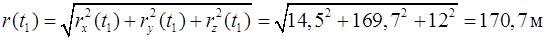 .
.
2. Динамика
Инерция – явление сохранения скорости движения тел при отсутствии внешних воздействий.
Инертность – свойство тел сопротивляться изменению скорости под действием сил.
Первый закон Ньютона (определяет причины изменения движения): тело сохраняет состояние покоя (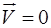 ) или движется равномерно и прямолинейно (
) или движется равномерно и прямолинейно (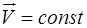 ), если векторная сумма всех сил, приложенных к телу, равна нулю (
), если векторная сумма всех сил, приложенных к телу, равна нулю (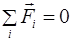 ).
).
|
|
|


