Средние скорости молекул идеального газа. 8 глава

,

.

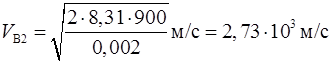Подставляя эти значения 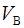в (3), и имея в виду, что , поскольку в задаче идет речь о скоростях, лежащих в интервале от до , получим

, .

Так как 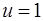, видим, что условие 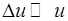выполняется для обеих температур. Теперь по формуле (2) найдем ответы

,

.

Замечание. Таким образом, при увеличении температуры наиболее вероятная скорость молекул увеличивается, а число молекул, скорости которых лежат в одном и том же интервале около наиболее вероятной, уменьшается. На графике, выражающем функцию распределения скоростей молекул , с увеличением температуры максимум кривой сдвигается вправо, а высота максимума уменьшается (рис.2.3).

Рис. 2.3

Задача 4. Пылинки массой взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается не более чем на 1 %. Температура 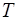воздуха во всем объеме одинакова и равна .

Решение. При равновесном распределении пылинок концентрация их зависит только от координаты 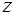по оси, направленной вертикально. В этом случае к распределению пылинок можно применить распределение Больцмана

. (1)

Так как в однородном поле силы тяжести , то

. (2)

По условию задачи, изменение концентрации с высотой мало по сравнению с 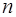, поэтому без существенной погрешности изменение концентрации можно заменить дифференциалом .

Дифференцируя выражение (2) по 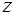, получим

.

Так как , то .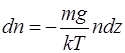

Отсюда находим изменение координаты:

.

Знак минус показывает, что положительным изменениям координаты соответствует уменьшение относительной концентрации . Знак минус опустим (в данном случае он несуществен)
и заменим дифференциалы и конечными приращениями и :

.

Произведя вычисления, найдем .

Как видно из полученного результата, концентрация даже таких маленьких пылинок () очень быстро изменяется с высотой.

 

Задача 5. Барометр в кабине летящего самолета все время показывает одинаковое давление , благодаря чему летчик считает высоту полета неизменной. Однако температура воздуха за бортом самолета изменилась с до . Какую ошибку в определении высоты допустил летчик? Давление 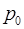у поверхности Земли считать нормальным.

Решение. Для решения задачи воспользуемся барометрической формулой

Барометр может показывать неизменное давление 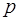при различных температурах и 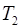за бортом только в том случае, если самолет находится не на высоте 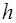(которую летчик считает неизменной), а на некоторой другой высоте .

Запишем барометрическую формулу для этих двух случаев:

; .

Найдем отношение и обе части полученного равенства прологарифмируем:

; .

Из полученных соотношений выразим высоты и и найдем их разность:

. (1)

.

Знак «минус» означает, что и, следовательно, самолет снизился на по сравнению с предполагаемой высотой.

 

Задача 6. Средняя длина свободного пробега 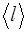молекулы углекислого газа при нормальных условиях равна . Определить среднюю арифметическую скорость 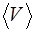молекул и число 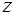соударений, которые испытывает молекула за .

Решение. Средняя арифметическая скорость молекул определяется по формуле

, (1)

где 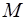– молярная масса вещества.

Подставив числовые значения, получим

Среднее число соударений молекулы за определяется отношением средней скорости 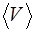молекулы к средней длине ее свободного пробега :

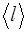(2)

Подставив в формулу (2) значения входящих в нее величин, получим .

 

Контрольная работа №2

Вариант	Номер задач

200. Колба вместимостью V = 0,5 л содержит газ при нормальных условиях. Определите число N молекул газа, находящихся в колбе.

201. В баллоне, объем которого V= 3 л находится кислород массой m = 4 г. Определите количество вещества и число молекул N газа.

202. Определить количество вещества водорода, находящегося в сосуде объемом V = 3 л при нормальных условиях, если плотность газа .

203. Сколько атомов содержится в газах массой 1 г каждый:

1) гелий; 2) углерод; 3) фтор; 4) полоний?

204. В сосуде вместимостью находится однородный газ при нормальных условиях. Количество вещества газа n = 0,2 моль, плотность r = 1,12 кг/м³. Определите, какой это газ?

205. В баллоне объемом V = 5 м³ находится перегретый водяной пар массой m = 10 кг при температуре . Рассчитайте давление пара в котле.

206. При нагревании идеального газа на при постоянном давлении его объем увеличился на 1/350 первоначального объема. Найдите начальную температуру газа.

207. Сухой воздух состоит в основном из кислорода и азота. Если пренебречь остальными составными частями воздуха, то можно считать, что массовые доли кислорода и азота соответственно равны . Определите молекулярную массу М_возд воздуха.

208. В баллонах объемом V ₁ = 20 л и V ₂ = 44 л содержится газ. Давление в первом баллоне p ₁ = 2,4 МПа, во втором p ₂ = 1,6 МПа. Определите общее давление р и парциальные и после соединения баллонов, если температура газа осталась прежней.

209. Смесь азота и водорода находится в сосуде объемом V = 15 л при температуре и давлении p = 200 МПа Рассчитайте массу смеси m и массы ее компонентов m₁ и m₂, если массовая доля азота = 0,7.

210. Каковы удельные теплоемкости C_V и C_p смеси газов, содержащей кислород массой m ₁= 10 г и азот массой m ₂ = 20 г?

211. Рассчитайте удельные теплоемкости C_V и C_p газов:

1) гелия; 2) водорода; 3) углекислого газа.

212. Найти показатель адиабаты для смеси газов, содержащей гелий m ₁= 10 г и водород m ₂ = 4 г.

213. При адиабатическом сжатии газа его объем уменьшился в 10 раз, а давление увеличилось в 21,4 раза. Определите соотношение C_V / C_p теплоемкостей газа.

214. На нагревание кислорода массой m = 160 г было затрачено количество теплоты Q = 1,76 кДж. Температура газа увеличилась на =12 K. Как протекал процесс: при постоянном объеме или при постоянном давлении?

215. Водород массой m = 4 г был нагрет на =10 K при постоянном давлении. Определите работу А расширения газа.

216. Газ, занимавший объем V ₁ = 12 л под давлением p ₁ = 100 кПа, был изобарно нагрет от температуры T ₁ = 300 К до T ₂ = 400 К. Определите работу расширения газа.

217. При адиабатическом сжатии кислорода массой m = 1 кг совершена работа А = 100 кДж. Определите конечную температуру газа, если до сжатия кислород находился при температуре T ₁ = 300 К.

218. Азот массой m= 2 г, имевший температуру Т = 300 К, был адиабатно сжат так, что его объем уменьшился n= 10 раз. Определите конечную температуру Т₂ газа и работу А сжатия.

219. Кислород, занимавший объем V ₁=1м³­­ под давлением p ₁ =1,2 МПа адиабатно расширился до объема V ₂=10 м³. Определите работу А расширения газа.

220. При изохорическом нагреве азота массой m =5 кг температура изменилась на Т=150 K, Найдите:

1) изменение U внутренней энергии;

2) работу А, совершенную газом;

3)количество теплоты Q, сообщенное газу

221. Водород находится в баллоне вместимостью V ₁=10 м³ при давлении p ₁=100 кПа В результате давление водорода увеличилось на p =200 кПа. Определите:

1)изменение внутренней энергии;

2)работу А, совершенную газом;

3)количество теплоты Q, сообщенное газу.

222. Водород находится в баллоне вместимостью V ₁=20 м³ при температуре под давлением p ₁=0,4 МПа. Каковы будут температура и давление, если водороду сообщить количество теплоты Q= 6 кДж.

223. Кислород, находящийся при давлении p ₁=80 кПа, занимает объем V ₁=20 м³. В результате изобарического нагрева его объем увеличивается до V ₂=3 м³. Определите:

1) изменение внутренней энергии;

2) работу А, совершенную им при расширении;

3) количество теплоты Q, сообщенное газу.

224. При изобарическом нагреве азоту было сообщено количество теплоты Q = 21кДж. Определите работу А, которую совершилпри этом газ, и изменение его внутренней энергии.

225. Гелий массой m= 1г был нагрет на 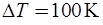при постоянном давлении р. Определите:

1)работу расширения А;

2)приращение внутренней энергии газа;

3)количество теплоты , переданное газу.

226. Какая доля количества теплоты , подводимая к идеальному газу при изобарном процессе, расходуется на увеличение внутренней энергии газа и какая доля - на работу А расширения?

Рассмотрите три случая, если газ:

1)одноатомный (i=3);

2)двухатомный (i= 5);

3)трехатомный (i= 6).

227. Азот массой m= 200 г изотермически расширяется при температуре , объем газа при этом увеличивается в два раза. Найдите:

1)изменение внутренней энергии;

2)работу А, совершенную при расширении газа;

3)количество теплоты , полученное газом.

228. Давление азота, объем которого V= 3 л, при нагревании увеличилось на p =1 МПа. Определите количество теплоты по лученное газом, если объем газа остался неизменным.

229. При адиабатном сжатии кислорода массой m = 20 г его внутренняя энергия увеличилась на U= 8 кДж, а температура повысилась до . Найдите: 1) повышение температуры ; 2) конечное давление газа , если начальное давление p ₁ = 200 кПа.

230. Идеальный двухатомный газ (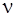 = 3 моль) занимающий объем V ₁ = 5 л и находящийся под давлением p ₁ = 1 МПа, подвергли изохорному нагреву до Т₂=500К. После этого газ изотермически расширился до начального давления, а затем он в результате изобарного сжатия вернулся в первоначальное состояние. Постройте график цикла в координатах Р – V и определите К.П. Д. цикла.

Рис.1

231. Идеальный газ совершает цикл, состоящий из трех последовательных процессов: изобарного, адиабатного и изотермического. В ходе адиабатного процесса газ нагревается от температуры до . Определите К.П.Д. цикла (рис. 1).

232. Идеальный газ совершает цикл Карно, КПД которого . Определите работу изотермического сжатия газа, если работу изотермического расширения составляет 400 Дж.

233. Идеальный газ совершает цикл Карно. Температура нагревателя , холодильника . Работа изотермического расширения газа составляет 2 кДж. Определите: 1)КПД цикла; 2)количество теплоты, отданное газом при изотермическом сжатии холодильнику.

234. Многоатомный идеальный газ совершает цикл Карно, при этом в процессе адиабатного расширения объем газа увеличивается в раза. Определите КПД цикла

235. Идеальный газ совершает цикл Карно. Температура нагревателя в три раза выше температуры холодильника Т₂. Нагреватель передал газу количество теплоты Q= 42 кДж. Какую работу А совершил газ?

236. Холодильная машина работает по обратимому циклу Карно в интервале температур . Рабочее тело азот, масса которого m = 0,2 кг. Найдите количество теплоты, отбираемое у охлажденного тела, если отношение максимального объема к минимальному .

237. Идеальный газ совершает цикл Карно. Температура нагревателя , охладителя . При изотермическом расширении газ совершает работу А = 100 Дж. Определите К.П.Д. цикла и количество теплоты , которое газ отдает холодильнику при изотермическом сжатии.

238. Идеальный газ совершает цикл Карно. Температура нагревателя в 4 раза выше температуры Т₂ холодильника. Какую долю 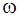количества теплоты, получаемого за один цикл от нагревателя, газ отдает холодильнику?

239.Идеальный двухатомный газ совершает цикл Карно (рис. 2). Объемы газа в состояниях В и С соответственно равны . Найдите К.П.Д. цикла.

Рис. 2.

240. При нагревании двух молей двухатомного идеального газа, его термодинамическая температура увеличилась в раза. Определите изменение энтропии, если нагревание происходит изохорно.

241. При нагревании двух молей двухатомного идеального газа, его термодинамическая температура увеличилась в раза. Определите изменение энтропии, если нагревание происходит изобарно.

242. Идеальный одноатомный газ (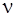 = 2 моль) сначала изобарно нагрели, так что объем газа увеличился в раза, а затем изохорно охладили так что давление газа уменьшилось в 2 раза. Определите приращение энтропии в ходе перечисленных процессов.

243.Азот массой адиабатно расширили в раза, а затем изобарно сжали до начального объема (рис. 3). Определите изменение энтропии в ходе указанных процессов.

Рис. 3.

244. В результате изохорного нагревания водорода массой давление газа увеличилось в два раза. Определите изменение энтропии газа.

245. Азот массой изобарно расширили от объема до . Найдите изменение энтропии.

246. Кислород массой m = 2кг изотермически расширился, увеличив свой объем в пять раз. Найдите изменение энтропии.

247. Водород массой был изобарно нагрет так, что объем его увеличился в 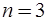раза, затем водород был изохорно охлажден так, что давление его уменьшилось в 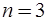раза. Найдите изменение энтропии в ходе указанных процессов.

248. При изохорическом нагреве одного моля двухатомного идеального газа его температура изменилась от , до . Найдите изменение энтропии газа.

249. При изобарном нагреве идеального трехатомного газа его температура изменилась от , до . Найдите изменение энтропии газа.

250. Используя закон распределения молекул идеального газа по скоростям, выведите формулу наиболее вероятной скорости V_в.

251. При какой температуре средняя квадратичная скорость молекул кислорода больше их наиболее вероятной скорости на 100 м/с.

252. Используя закон распределения молекул идеального газа по скоростям, найдите закон, выражающий распределение молекул газа по относительным скоростям .

253. Используя закон распределения молекул идеального газа по скоростям, найдите среднюю арифметическую скорость молекул..

254. Используя закон распределения молекул идеального газа по скоростям, найдите среднюю квадратичную скорость <V_кв>.

255. Используя функцию распределения молекул идеального газа по энергиям, найдите среднюю кинетическую энергию < Е > молекул.

256. На какой высоте давление воздуха составляет 60% от давления воздуха на уровне моря? Считайте, что температура воздуха везде одинакова и равна 10 °С.

257. Пылинки, взвешенные в воздухе, имеют массу . Во сколько раз уменьшится их концентрация при увеличении высоты на ? Температура воздуха Т = 300К.

258. Определите силу , действующую на частицу, находящуюся во внешнем однородном поле силы тяжести, если отношение концентраций частиц на двух уровнях, отстоящих друг от друга на , равно . Температуру Т считать везде одинаковой и равной 300К.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: