 |
Определение вектора. Виды векторов
|
|
|
|
Математические или физические величины, которые характеризуются только числом, измеряющим их в определенных единицах меры, называют скалярными или скалярами. Скалярами являются, например масса, объем и т.п.
Кроме скалярных величин существуют величины векторные (скорость, ускорение, сила и т.п.)
Вектором называется величина, которая характеризуется числом, измеряющим ее в определенных единицах меры, и направлением в пространстве. Обозначается вектор или буквой со стрелкой  , или жирной буквой a.
, или жирной буквой a.
Число  , измеряющее вектор в определенных единицах меры, называется модулем или длиной вектора. Зачастую
, измеряющее вектор в определенных единицах меры, называется модулем или длиной вектора. Зачастую  обозначают простой буквой а.
обозначают простой буквой а.
Геометрически вектор изображают отрезком со стрелкой. Направление стрелки указывает направление вектора в пространстве, а длина отрезка изображает модуль вектора (см. рис. 1а).

Рис. 1
Два вектора называются равными, если равны их длины и совпадают направления.
Вектор, длина которого равна нулю, называется нулевым. Его направление не определено.
Вектор, длина которого равна единице, называется единичным.
Вектор  называется противоположным вектору
называется противоположным вектору  , так как его длина равна длине вектора
, так как его длина равна длине вектора  и он имеет обратное направление.
и он имеет обратное направление.
Единичный вектор 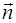 расположенный параллельно вектору
расположенный параллельно вектору  , может быть определен соотношением
, может быть определен соотношением  . Соответственно, любой вектор может быть представлен в виде
. Соответственно, любой вектор может быть представлен в виде  .
.
Проекцией вектора  на направление единичного вектора
на направление единичного вектора  называется вектор
называется вектор  , направление которого совпадает с направлением единичного вектора
, направление которого совпадает с направлением единичного вектора 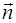 , а длина
, а длина  равна произведению длины вектора
равна произведению длины вектора  на косинус угла между векторами
на косинус угла между векторами  и
и 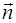 (см. рис. 2):
(см. рис. 2):
 , где
, где 

Рис.2
В зависимости от видов допускаемых инвариантных [†] преобразований векторы как математическое понятие могут быть разделены на три типа.
|
|
|
1. Простые векторы, которые обычно мы называем одним словом вектор. Инвариантным преобразованием для векторов является параллельный перенос в произвольном направлении (см. рис.1.а).
2. Аксиальные векторы. Эти векторы могут располагаться только вдоль определенного направления (см. рис. 1.б). Инвариантным преобразованием для аксиального вектора является его перенос вдоль этого направления.
3. Радиус – вектор соединяет начало координат с точкой, имеющей определенные координаты x, y, z. Для радиус – вектора ни параллельный перенос, ни вращение инвариантными преобразованиями не являются.
Сложение и вычитание векторов
Суммой двух векторов  и
и 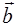 называется вектор, совпадающий с замыкающей стороной треугольника, построенного на данных двух векторах (см. рис. 1.а).
называется вектор, совпадающий с замыкающей стороной треугольника, построенного на данных двух векторах (см. рис. 1.а).
 Рис.4
Рис.4
Правило сложения векторов:
1.  ,
,
2. 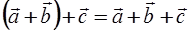 .
.
Эти законы позволяют находить сумму любого числа векторов. На рис. 3.б приведено сложение четырех векторов.
Если многоугольник, построенный на данных векторах, окажется замкнутым так, что конец последнего слагаемого вектора совпадет с началом первого слагаемого, то сумма данных векторов будет равна нулю. И обратно, если сумма некоторых векторов равна нулю, то построенный на этих векторах многоугольник будет замкнутым.
Разностью  двух векторов называется сумма вектора
двух векторов называется сумма вектора  с вектором
с вектором  , противоположным вектору
, противоположным вектору 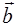 (см. рис. 4):
(см. рис. 4):

 .
.

Рис.4
Умножение вектора на число
Произведением скаляра  на вектор
на вектор  называется вектор, длина которого равна
называется вектор, длина которого равна  , а направление его совпадает с направлением
, а направление его совпадает с направлением  , если
, если  , и противоположно
, и противоположно  , если
, если  . Произведение вектора на скаляр подчиняется законам умножения чисел:
. Произведение вектора на скаляр подчиняется законам умножения чисел:
 .
.
Произведение векторов
Из двух векторов можно образовать два существенно различных произведения: скалярное и векторное.
Скалярное произведение
|
|
|
Скалярным произведением двух векторов  и
и 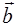 называется произведение модулей этих векторов на косинус угла между этими векторами:
называется произведение модулей этих векторов на косинус угла между этими векторами:  . Эквивалентной формой записи скалярного произведения является выражение
. Эквивалентной формой записи скалярного произведения является выражение  .
.
Пусть 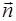 - единичный вектор,
- единичный вектор,  , тогда
, тогда  , т.е. скалярное произведение любого вектора
, т.е. скалярное произведение любого вектора  на единичный вектор
на единичный вектор 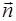 определяет величину проекции вектора на направление этого единичного вектора.
определяет величину проекции вектора на направление этого единичного вектора.
Скалярное произведение векторов обладает следующими свойствами:
1. 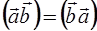 ;
;
2. 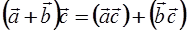 .
.
Если векторы  и
и 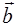 взаимно перпендикулярны, то их скалярное произведение
взаимно перпендикулярны, то их скалярное произведение  . И обратно, если скалярное произведение двух отличных от нуля векторов равно нулю, то эти векторы взаимно перпендикулярны.
. И обратно, если скалярное произведение двух отличных от нуля векторов равно нулю, то эти векторы взаимно перпендикулярны.
Векторное произведение
Векторным произведением двух векторов  и
и 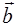 называется
называется
вектор  или в эквивалентной форме
или в эквивалентной форме  , который
, который
а) направлен перпендикулярно плоскости, в которой лежат вектора  и
и 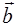 , в сторону поступательного перемещения правого винта, если его вращать от первого сомножителя ко второму в направлении наименьшего угла между векторами;
, в сторону поступательного перемещения правого винта, если его вращать от первого сомножителя ко второму в направлении наименьшего угла между векторами;
б) имеет длину, равную произведению длин векторов  и
и 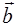 на синус угла между ними (см. рис. 1):
на синус угла между ними (см. рис. 1):  .
.
Векторное произведение обладает следующими свойствами:
 ;
;
 ;
;
 .
.

Рис.5
Произведение трех векторов
Из трех произвольных векторов 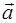 и
и  и
и  можно образовать два существенно различных произведения: смешанное и двойное векторное произведение.
можно образовать два существенно различных произведения: смешанное и двойное векторное произведение.
Смешанное произведение трех векторов
Смешанным произведением трех векторов  ,
, 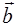 и
и  называется скалярное произведение одного из них на векторное произведение двух других:
называется скалярное произведение одного из них на векторное произведение двух других:
 .
.
Абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих трех векторах.
С помощью смешанного произведения трех векторов решается вопрос об их компланарности.
Векторы называются компланарными, если они лежат либо в одной плоскости, либо в параллельных плоскостях. Очевидно, любые два вектора являются компланарными.
Три вектора не всегда компланарны. Для того, чтобы три вектора были компланарными необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Двойное векторное произведение
Двойным векторным произведением  трех векторов называется векторное произведение одного из них на векторное произведение двух других. Вектор, получившийся в результате двойного векторного произведения
трех векторов называется векторное произведение одного из них на векторное произведение двух других. Вектор, получившийся в результате двойного векторного произведения  , лежит в плоскости векторов
, лежит в плоскости векторов 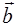 и
и  и может быть представлен выражением
и может быть представлен выражением
|
|
|
 .
.
Координатная форма представления векторов
В системе координат XYZопределим единичные векторы в направлении OX, OYи OZкак  . Тогда произвольный вектор
. Тогда произвольный вектор  может быть представлен в виде суммы трех взаимно перпендикулярных векторов, направленных по осям координат:
может быть представлен в виде суммы трех взаимно перпендикулярных векторов, направленных по осям координат:  ,
,
где скаляры  - проекции вектора
- проекции вектора  на координатные оси OX, OYи OZсоответственно.
на координатные оси OX, OYи OZсоответственно.
Векторы  и
и  взаимно перпендикулярны друг другу, поэтому для них выполняются соотношения:
взаимно перпендикулярны друг другу, поэтому для них выполняются соотношения:
 ;
;
 .
.
Радиус – вектор, проведенный из начала координат в некоторую точку М с координатами (x;y;z), также может быть определен в координатной форме (рис.6): 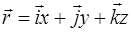 .
.

Рис.6
Правила действия над векторами, заданными в координатной форме:
 ,
,
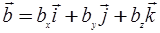 ,
,
 .
.
1. Сложение и вычитание.

2. Скалярное произведение.
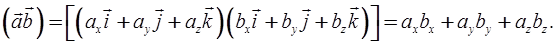
3. Векторное произведение.

Из формул для скалярного произведения двух векторов можно получить формулу для вычисления модуля произвольного вектора  :
:
 .
.
С другой стороны,
 .
.
Поэтому  .
.
Если  - единичный вектор. Тогда его проекциями на оси координат будут косинусы углов
- единичный вектор. Тогда его проекциями на оси координат будут косинусы углов  , образованных единичным вектором с осями координат OX, OY, OZсоответственно. Из предыдущей формулы, записанной для случая единичного вектора, получим условие
, образованных единичным вектором с осями координат OX, OY, OZсоответственно. Из предыдущей формулы, записанной для случая единичного вектора, получим условие 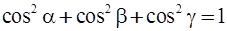 .
.
Отметим, что направляющие косинусы можно определить и для любого произвольного вектора  :
:
 .
.
Из формулы для скалярного произведения двух векторов можно получить также выражение, определяющее косинус угла между этими векторами:
 .
.
Формулы дифференциального исчисления
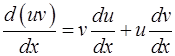




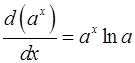
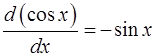


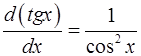
Формулы интегрального исчисления
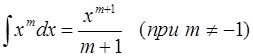










Соотношение между внесистемными единицами и единицами СИ
| Длина | 1 ангстрем ( ) = ) = 
|
| Время | 1 сут = 86400 с, 1 год = 365,25 сут = 
|
| Плоский угол | 
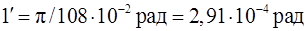

|
| Объем, вместимость | 
|
| Масса |  , , 
|
| Сила | 
|
| Работа, энергия |  , ,  , ,

|
| Мощность | 
|
| Давление |  , ,  , ,
 , , 
|
| Напряжение (механическое) | 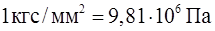
|
| Частота вращения |  , , 
|
| Концентрация частиц | 
|
| Теплота (количество теплоты) |  , ,

|
|
|
|
Эффективный диаметр молекул, динамическая вязкость и теплопроводность газов при нормальных условиях
| Вещество | Эффективный диаметр 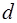 , , 
| Динамическая вязкость  , , 
| Теплопроводность 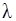 , , 
|
| Азот Аргон Водород Воздух Гелий Кислород Пары воды | 0,38 0,35 0,28 – 0,22 0,36 – | 16,6 21,5 8,66 17,2 – 19,8 8,32 | 24,3 16,2 24,1 – 24,4 15,8 |
Динамическая вязкость  жидкостей при
жидкостей при 
Вода …………………..……………….…… 1,00
Глицерин ………………………………….. 1480
Масло касторовое ………………….……… 987
Масло машинное ………………………….. 100
Ртуть ……………………….…………….… 1,58
Основные физические постоянные
(округленные с точностью до трех значащих цифр)
Нормальное ускорение свободного падения ……….. 
Гравитационная постоянная …………… 
Постоянная Авогадро ………………..……… 
Молярная газовая постоянная ……………. 
Стандартный объем *………………………. 
Постоянная Больцмана ………………………. 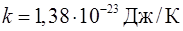
Атомная единица массы ………………...…… 
* Молярный объем идеального газа при нормальных условиях
[*] Бесконечно малый угол поворота, может быть представлен в виде вектора, направленного вдоль оси вращения. Это возможно, когда радиус-вектор можно считать неизменным. Определение векторного произведения двух векторов см. в приложении (стр. 103).
[†] Инвариантностью в математике называется свойство неизменности по отношению какому либо преобразованию (условию) или совокупности преобразований.
|
|
|


