 |
Средние скорости молекул идеального газа. 6 глава
|
|
|
|
 , (1.4)
, (1.4)
где  – масса молекулы.
– масса молекулы. 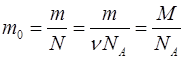 .
.
Замечание: для решения задач полагают, что молярная масса воздуха  .
.
Идеальный газ – это модель, которая удовлетворяет следующим требованиям:
– суммарный объем всех молекул газа  ;
;
– молекулы газа сталкиваются друг с другом и со стенками сосуда как идеально упругие шарики; на расстоянии молекулы газа не взаимодействуют ни друг с другом, ни с другими телами.
При нормальных условиях*, т.е. при не очень больших давлениях и не очень низких температурах, любой газ с хорошей
*Нормальные условия:  ;
;  ;
;  .
.
степенью точности можно считать идеальным.
Уравнение состояния идеального газа:
 . (1.5)
. (1.5)
Величина этой константы для 1 моля идеального газа называется универсальной газовой постоянной  :
:
 .
.
Если газ содержит  молей, уравнение состояния идеального газа (или уравнение Менделеева-Клапейрона) имеет вид
молей, уравнение состояния идеального газа (или уравнение Менделеева-Клапейрона) имеет вид
 или
или  . (1.6)
. (1.6)
Постоянная Больцмана  .
.
 , (1.7)
, (1.7)
где  – число молекул газа.
– число молекул газа.
Концентрация молекул газа:
 . (1.8)
. (1.8)
С учетом выражения (1.8) уравнение состояния (1.7) можно переписать в виде
 . (1.9)
. (1.9)
Закон Дальтона: давление смеси газов равно сумме парциальных давлений компонентов смеси:
 , (1.10)
, (1.10)
где 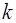 – число компонентов смеси,
– число компонентов смеси,  – парциальное давление каждого газа в отдельности в объеме
– парциальное давление каждого газа в отдельности в объеме 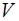 (
( ,
,  – число молекул
– число молекул  -го компонента смеси).
-го компонента смеси).
Закон Авогадро. Равные объемы идеальных газов при одинаковых температуре и давлении содержат одинаковое число молекул.
Макросистема (или термодинамическая система) – система, состоящая из очень большого числа частиц (молекул, атомов и др.). Например, газ.
Макропараметры состояния системы – давление, объем, температура, концентрация и т.д.
Микропараметры системы – средние значения скоростей молекул газа, средние значения энергии молекул и т.д.
|
|
|
Равновесное состояние термодинамической системы – это состояние, при котором макропараметры (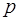 ,
, 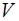 ,
, 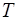 ) имеют постоянные значения для любой части системы. Равновесное состояние можно представить точкой на диаграмме, по координатным осям откладываются значения
) имеют постоянные значения для любой части системы. Равновесное состояние можно представить точкой на диаграмме, по координатным осям откладываются значения 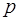 ,
, 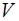 ,
, 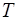 (рис. 1.1).
(рис. 1.1).
Процесс – переход макросистемы из одного состояния в другое, например, благодаря внешнему воздействию. Если воздействие осуществляется достаточно медленно, то процесс называют равновесным. Он может быть изображен на диаграмме  как последовательность точек, соответствующих промежуточным равновесным состояниям системы.
как последовательность точек, соответствующих промежуточным равновесным состояниям системы.
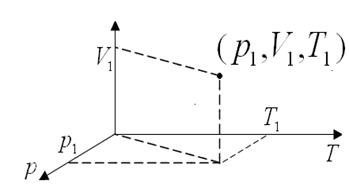
| Рис. 1.1. Изображение равновесного состояния системы в виде точки с координатами 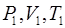 на диаграмме на диаграмме 
|

| Рис. 1.2 Процесс равновесного перехода системы из состояния 1 с макропараметрами  в состояние 2 с макропараметрами в состояние 2 с макропараметрами  на диаграмме на диаграмме 
|
Изопроцессы – процессы идеальных газов, происходящие при неизменном значении одного из параметров 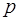 ,
, 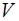 или
или 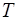 (рис. 1.3).
(рис. 1.3).
Теплоемкость  – это количество тепла, которое нужно сообщить телу (газу), чтобы повысить его температуру на один Кельвин:
– это количество тепла, которое нужно сообщить телу (газу), чтобы повысить его температуру на один Кельвин:
 . (1.11)
. (1.11)
Величина теплоемкости зависит от способа, которым системе сообщают тепло, т.е. различна для различных процессов. Теплоемкость измеряется в  .
.
Молярная теплоемкость  – величина, равная количеству теплоты необходимому для нагревания одного моля вещества на 1 К.
– величина, равная количеству теплоты необходимому для нагревания одного моля вещества на 1 К.
 . (1.12)
. (1.12)
Молярная теплоемкость  измеряется в
измеряется в  .
.

Рис. 1.3. Изопроцессы в идеальных газах
Удельная теплоемкость вещества – величина, равная количеству теплоты необходимому для нагревания 1кг вещества на 1 К:
 . (1.13)
. (1.13)
Удельная теплоемкость измеряется в  .
.
Удельная теплоемкость 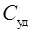 связана с молярной
связана с молярной  соотношением:
соотношением:
 (1.14)
(1.14)
Политропический процесс – процесс, протекающий с постоянной теплоемкостью:  .
.
Молярные теплоемкости при постоянном объеме  и постоянном давлении
и постоянном давлении  :
:
 ,
,  (1.15)
(1.15)
где  – число степеней свободы молекул газа.
– число степеней свободы молекул газа.
|
|
|
У молекул одноатомного газа  три степени свободы поступательного движения (рис.1.4). Молекула двухатомного газа, кроме трех степеней свободы поступательного движения, имеет еще две степени свободы вращательного движения (рис.1.5). У молекул двухатомного газа пять степеней свободы
три степени свободы поступательного движения (рис.1.4). Молекула двухатомного газа, кроме трех степеней свободы поступательного движения, имеет еще две степени свободы вращательного движения (рис.1.5). У молекул двухатомного газа пять степеней свободы  . Трехатомные и многоатомные молекулы газа имеют шесть степеней свободы
. Трехатомные и многоатомные молекулы газа имеют шесть степеней свободы  : три степени свободы поступательного движения и три степени свободы вращательного движения (рис.1.6).
: три степени свободы поступательного движения и три степени свободы вращательного движения (рис.1.6).

| 
| 
|
| Рис. 1.4. Одноатомная молекула имеет три поступательные степени свободы | Рис. 1.5. Двухатомная молекула имеет три поступательные и две вращательные степени свободы | Рис.1. 6. Трехатомная молекула имеет три поступательные и три вращательные степени свобод. |
Уравнение Майера:
 (1.16)
(1.16)
Внутренняя энергия идеального газа равна суммарной кинетической энергии хаотического движения всех 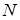 молекул газа:
молекул газа:
 (1.17)
(1.17)
или
 , (1.18)
, (1.18)
где  – масса молекулы газа;
– масса молекулы газа;  – средняя скорость молекул газа;
– средняя скорость молекул газа;  – средняя кинетическая энергия молекулы газа,
– средняя кинетическая энергия молекулы газа,  – количество вещества.
– количество вещества.
Работа, совершаемая идеальным газом при переходе из состояния 1 в состояние 2,
 . (1.19)
. (1.19)
Первое начало термодинамики: теплота, сообщаемая изолированной системе, идет на изменение внутренней энергии системы и на совершение системой работы над внешними телами (против внешних сил):
 (1.20)
(1.20)
Для конечных изменений термодинамических параметров:
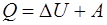 . (1.21)
. (1.21)
При поглощении системой тепла  , при выделении
, при выделении  .
.
При расширении системы 
 , при сжатии
, при сжатии  .
.
При нагревании системы 
 , при охлаждении
, при охлаждении  .
.
Изотермический процесс:  или
или  (рис.1.7). Закон Бойля – Мариотта:
(рис.1.7). Закон Бойля – Мариотта:

|
Рис.1.7. Изотермический процесс перехода системы из состояния 1 в состояние 2 в координатах 
|
 . (1.22)
. (1.22)
Работа при изотермическом процессе:
 . (1.23)
. (1.23)
Внутренняя энергия 
 . (1.24)
. (1.24)
Изохорический процесс -  или
или  (рис.1.8).
(рис.1.8).

| Рис.1.8. Изохорический процесс перехода системы из состояния 1 в состояние 2 в координатах 
|
Закон Шарля:
 . (1.25)
. (1.25)
Работа при изохорическом процессе 
 .
.
Изменение внутренней энергии при изохорическом процессе
 . (1.26)
. (1.26)
 .
.
Изобарический процесс - 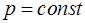 или
или 

| Р ис. 1.9. Изобарический процесс перехода системы из состояния 1 в состояние 2 в координатах 
|
Закон Гей-Люссака:
 (1.27)
(1.27)
 (1.28)
(1.28)
 (1.29)
(1.29)
 , (1.30)
, (1.30)
|
|
|
т.к. из уравнения Менделеева – Клапейрона:
 .
.
Адиабатический процесс – процесс, происходящий без передачи тепла,  . Теплоемкость газа при таком процессе
. Теплоемкость газа при таком процессе  .
.
 . (1.31)
. (1.31)
 . (1.32)
. (1.32)
Подставив (2.1.32) в (2.1.31) получим уравнение адиабатического процесса
 , (1.33)
, (1.33)
 , (1.34)
, (1.34)
где  – показатель адиабаты. После интегрирования выражения (1.34), получим
– показатель адиабаты. После интегрирования выражения (1.34), получим

или
 . (1.35)
. (1.35)

| Рис.1.10. Адиабатический процесс перехода системы из состояния 1 в состояние 2 в координатах  . Адиабата ( . Адиабата (  ) идет круче, чем изотерма ( ) идет круче, чем изотерма (  ) )
|
Уравнения Пуассона:
 (1.36)
(1.36)
Коэффициент полезного действия (к.п.д.) циклического процесса равен отношению произведенной за цикл работы  к полученному от нагревателя теплу
к полученному от нагревателя теплу
 , (1.37)
, (1.37)
где  - количество теплоты, полученное телом (газом) от нагревателя;
- количество теплоты, полученное телом (газом) от нагревателя; 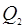 - количество теплоты, переданное рабочим телом холодильнику.
- количество теплоты, переданное рабочим телом холодильнику.
Цикл Карно – это циклический процесс, при котором прием тепла от нагревателя и передача тепла холодильнику обратимы. Этот цикл состоит из двух адиабат и двух изотерм (рис.1.11)
К.п.д. цикла Карно
 . (1.38)
. (1.38)

| Рис.1.11. Цикл Карно.
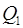 – количество теплоты, полученное системой от нагревателя. – количество теплоты, полученное системой от нагревателя.
 – количество теплоты, отданное системой холодильнику. – количество теплоты, отданное системой холодильнику.
 , ,  – адиабаты, – адиабаты,
 , ,  – изотермы – изотермы
|
Энтропия (S) – это функция состояния термодинамической системы, дифференциалом  которой является соотношение.
которой является соотношение.
 (1.39)
(1.39)
 , (1.40)
, (1.40)
где подынтегральное выражение и пределы интегрирования необходимо выразить через величины, характеризующие исследуемый процесс.
 . (1.41)
. (1.41)
Формулы (1.40) и (1.41) определяют энтропию с точностью до аддитивной постоянной. Физический смысл имеет не сама энтропия, а ее изменение, т.е. разность энтропий.
Приращение энтропии идеального газа:
 . (1.42)
. (1.42)
Первое начало термодинамики для идеального газа с учетом (1.41):
 . (1.43)
. (1.43)
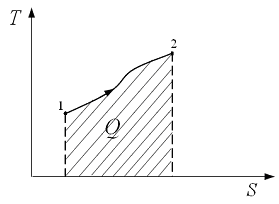 Рис.1.12
Рис.1.12
| Тепло, полученное системой в результате процесса  , ,
 , (1.44)
равно площади под кривой процесса на диаграмме , (1.44)
равно площади под кривой процесса на диаграмме  (рис. 1.12). (рис. 1.12).
|
Неравенство Клаузиуса
 , (1.45)
, (1.45)
т.е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).
Примеры решения задач.
Задача 1. Найти молярную массу  смеси кислорода
смеси кислорода  массой
массой  и азота
и азота  массой
массой  .
.
|
|
|
Решение. Молярная масса смеси  равна отношению массы смеси
равна отношению массы смеси  к количеству вещества смеси
к количеству вещества смеси  :
:
 . (1)
. (1)
Масса смеси  , количество вещества смеси равно сумме количеств вещества компонентов
, количество вещества смеси равно сумме количеств вещества компонентов
 , (2)
, (2)
где  и
и  ,
,  ,
,  .
.
 ,
,
 .
.
Задача 2. В баллоне объемом  находится гелий под давлением
находится гелий под давлением  при температуре
при температуре  . После того как из баллона было израсходовано
. После того как из баллона было израсходовано 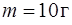 гелия, температура в баллоне понизилась до
гелия, температура в баллоне понизилась до  . Определите давление
. Определите давление  , оставшегося в баллоне гелия. Молярная масса гелия
, оставшегося в баллоне гелия. Молярная масса гелия  .
.
Решение. Для начального и конечного состояний гелия уравнение Менделеева – Клапейрона имеет вид
 , (1)
, (1)
 , (2)
, (2)
где  и
и  – масса гелия в начальном и конечном состояниях.
– масса гелия в начальном и конечном состояниях.
Из (1) и (2) выразим  и
и  :
:
 ,
,  , (3)
, (3)
 . (4)
. (4)
Отсюда найдем искомое давление.
 , (5)
, (5)
 .
.
Задача 3. Определить количество теплоты, поглощаемой водородом массой  при нагревании его от температуры
при нагревании его от температуры  до температуры
до температуры  при постоянном давлении. Найти также изменение внутренней энергии газа и совершаемую им работу.
при постоянном давлении. Найти также изменение внутренней энергии газа и совершаемую им работу.
Решение. Количество теплоты, поглощаемое газом при изобарном нагревании,
 , (1)
, (1)
где  – масса нагреваемого газа,
– масса нагреваемого газа, 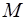 – его молярная масса. Для водорода
– его молярная масса. Для водорода  .
. 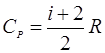 – теплоемкость при постоянном давлении,
– теплоемкость при постоянном давлении,  – число степеней свободы. Для молекулы водорода
– число степеней свободы. Для молекулы водорода 
 .
.  – изменение температуры газа.
– изменение температуры газа.
 .
.
Изменение внутренней энергии газа
 , (2)
, (2)
 .
.
Работа расширения, в соответствии с первым началом термодинамики,
 , (3)
, (3)
 .
.
Задача 4. Один моль идеального двухатомного газа находится под давлением  и занимает объем
и занимает объем  . Сначала газ изохорно нагревают до температуры
. Сначала газ изохорно нагревают до температуры  , затем, изотермически расширяя, доводят его до первоначального давления. После этого путем изобарного сжатия возвращают газ в начальное состояние. Определить к.п.д.
, затем, изотермически расширяя, доводят его до первоначального давления. После этого путем изобарного сжатия возвращают газ в начальное состояние. Определить к.п.д.  цикла.
цикла.
Решение. Построим график цикла в координатах  . Он состоит из изохоры
. Он состоит из изохоры  , изотермы
, изотермы  и изобары
и изобары  (рис.1.13).
(рис.1.13).
 Рис. 1.13
Рис. 1.13
| Работа, совершаемая газом за цикл, равна площади цикла (заштрихована) и равна разности
 . (1)
Газ получает тепло . (1)
Газ получает тепло  на двух участках: на двух участках:  и и  , т.е. , т.е.
 (2) (2)
|
Количество теплоты, полученное газом при изохорном  процессе
процессе  ,
,
 , (3)
, (3)
где  ,
,  . Для двухатомного газа
. Для двухатомного газа  . Температуру газа в состоянии 1 найдем из уравнения Менделеева – Клапейрона
. Температуру газа в состоянии 1 найдем из уравнения Менделеева – Клапейрона
 , (4)
, (4)
 .
.
Количество теплоты, полученное газом при изотермическом процессе, равно
 , (5)
, (5)
где  - объем, занимаемый газом при температуре
- объем, занимаемый газом при температуре  и давлении
и давлении 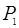 (точка 3 на графике).
(точка 3 на графике).
|
|
|


