 |
Средние скорости молекул идеального газа. 3 глава
|
|
|
|
Решение. По второму закону Ньютона модуль силы равен
 ,
,
где  – ускорение. Первая производная пути по времени – это скорость тела:
– ускорение. Первая производная пути по времени – это скорость тела:
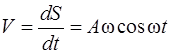 .
.
Производная скорости по времени – ускорение:  .
.
Закон изменения силы  :
:

Подставив числовые значения:  ,
, 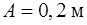 ,
,  и
и 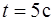 получим: (
получим: ( ,
,  )
)  .
.
Задача 2. Груз массой  вращается на канате длиной
вращается на канате длиной  в горизонтальной плоскости, совершая
в горизонтальной плоскости, совершая  (рис. 2.12). Какой угол с вертикалью образует канат и какова сила его натяжения.
(рис. 2.12). Какой угол с вертикалью образует канат и какова сила его натяжения.
Решение. На груз действуют сила тяжести  и сила натяжения каната
и сила натяжения каната  (рис. 2.12). По второму закону Ньютона
(рис. 2.12). По второму закону Ньютона
 . (1)
. (1)
 Рис. 2.12
Рис. 2.12
| Так как движение по окружности происходит здесь с постоянной по модулю скоростью, то полное ускорение тела равно нормальному ускорению

|
Выберем оси  и
и  как показано на рис. 2.12. Проектируя векторы, входящие в уравнение (1) на эти оси, получим
как показано на рис. 2.12. Проектируя векторы, входящие в уравнение (1) на эти оси, получим
 , (2)
, (2)
 . (3)
. (3)
Из рис.2.12 видно, что радиус окружности равен
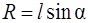 . (4)
. (4)
Решив совместно уравнения (2), (3) и (4), получим
 , (5)
, (5)
 . (6)
. (6)
Подставив числовые значения  ,
,  ,
,  в формулы (5) и (6), получим
в формулы (5) и (6), получим  ,
,  ,
,  .
.
Задача 3.
Через блок, укрепленный на потолке комнаты, перекинута нить, на концах которой подвешены грузы с массами  и
и  . Массы блока и нити пренебрежимо малы, трением можно пренебречь. Найти ускорение центра масс этой системы.
. Массы блока и нити пренебрежимо малы, трением можно пренебречь. Найти ускорение центра масс этой системы.
Решение. Силы, действующие на тела, показаны на рис. 2.13. Предположим, что ускорение первого груза направлено вниз, а второго груза – вверх. Второй закон Ньютона в проекции на ось  для каждого тела в отдельности
для каждого тела в отдельности
 , (1)
, (1)
 . (2)
. (2)
 Рис. 2.13
Рис. 2.13
| Т.к. 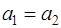 , то из уравнений (1) и (2) сила натяжения нити Т равна , то из уравнений (1) и (2) сила натяжения нити Т равна
 Проекцию ускорения центра масс
Проекцию ускорения центра масс  этой системы на ось y определим из уравнения этой системы на ось y определим из уравнения

|
 .
.
Подставив числовые значения  ,
,  , получим:
, получим:
 .
.
Задача 4.
В вагоне укреплен отвес (шарик массой m на нити). Какое направление примет отвес, если вагон скатывается без трения с наклонной плоскости, образующей с горизонтом угол  (рис.2.14). Отвес считать неподвижным относительно вагона.
(рис.2.14). Отвес считать неподвижным относительно вагона.
|
|
|
 Рис. 2.14
Рис. 2.14
| Решение. По второму закону Ньютона для шарика:
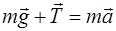 , (1)
где , (1)
где  – ускорение шарика, равное ускорению вагона. Вагону сообщает ускорение составляющая его силы тяжести, направленная вдоль наклонной плоскости – ускорение шарика, равное ускорению вагона. Вагону сообщает ускорение составляющая его силы тяжести, направленная вдоль наклонной плоскости  , где , где 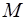 – масса вагона. – масса вагона.
|
По второму закону Ньютона для вагона:
 , (2)
, (2)
 . (3)
. (3)
Уравнение (1) в проекциях на ось х, совпадающую с направлением ускорения  , примет вид
, примет вид
 , (4)
, (4)
отсюда  .
.
Так как сила натяжения нити  , то
, то  и
и  .
.
При спуске вагона отвес расположен по нормали к наклонной плоскости.
Задача 5.
Небольшое тело пустили снизу вверх по наклонной плоскости, составляющей угол  с горизонтом. Найти коэффициент трения, если время подъема тела оказалось в два раза меньше времени спуска.
с горизонтом. Найти коэффициент трения, если время подъема тела оказалось в два раза меньше времени спуска.
Решение. Силы, действующие на тело при его движении вверх, показаны на рис. 2.15. Второй закон Ньютона в проекции на оси x,y имеет вид
 , (1) , (1)
 , (2) , (2)
 , (3)
где , (3)
где 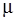 – коэффициент трения. – коэффициент трения.
|  Рис. 2.15
Рис. 2.15
|
Подставив (3) в (1) получим 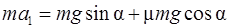 .
.
Т.е. тело движется вверх равнозамедленно с ускорением  :
:
 , (4)
, (4)
а уравнение его движения имеет вид
 , (5)
, (5)
где  – начальная скорость тела. Время движения тела вверх
– начальная скорость тела. Время движения тела вверх  определим из условия:
определим из условия:
 ,
,  , (6)
, (6)
а координата точки поворота  .
.
При движении тела вниз меняется направление силы трения и, следовательно, вниз тело движется с ускорением
 , (7)
, (7)
а уравнение его движения имеет вид
 .
.
Время движения тела вниз 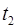 определим из условия
определим из условия
 ,
,
 . (8)
. (8)
Отношение  по условию. Подставив (4), (6), (7) в (8), имеем
по условию. Подставив (4), (6), (7) в (8), имеем
 ,
,


Подставив численные данные задачи, получим  .
.
Задача 6. Однородный шар массы  скатывается без проскальзывания по наклонной плоскости, составляющей угол
скатывается без проскальзывания по наклонной плоскости, составляющей угол 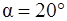 с горизонтом (рис. 2.16). Найти кинетическую энергию шара через
с горизонтом (рис. 2.16). Найти кинетическую энергию шара через  после начала движения.
после начала движения.
Решение. Кинетическая энергия шара равна сумме кинетической энергии поступательного движения центра масс шара и кинетической энергии вращательного движения шара относительно неподвижной оси: 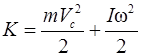 ,
,
|
|
|
где  – момент инерции шара,
– момент инерции шара, 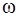 – угловая скорость вращения шара.
– угловая скорость вращения шара.
Скорость центра масс шара  , где
, где  – ускорение центра масс шара, которое найдем следующим образом: уравнение второго закона Ньютона в проекции на ось
– ускорение центра масс шара, которое найдем следующим образом: уравнение второго закона Ньютона в проекции на ось  (см. рис. 2.16):
(см. рис. 2.16):
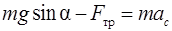 .
.
Основное уравнение вращательного движения шара относительно оси проходящей через центр масс шара:

или  .
.
Т.к. в отсутствие проскальзывания  , а ускорение
, а ускорение  .
.

Рис. 2.16
Получив систему двух уравнений,
 ,
,
находим ускорение 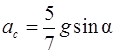 ,
,
скорость центра масс шара  ,
,
и угловую скорость вращения шара
 .
.
Кинетическая энергия шара в момент времени 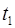 будет равна
будет равна
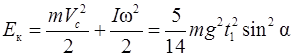 .
.
 .
.
Задача 7. Круглая платформа радиуса 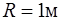 , момент инерции которой
, момент инерции которой  , вращается по инерции вокруг вертикальной оси с частотой
, вращается по инерции вокруг вертикальной оси с частотой  . На краю платформы стоит человек, масса которого
. На краю платформы стоит человек, масса которого  . Сколько оборотов в секунду
. Сколько оборотов в секунду 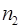 будет совершать платформа, если человек перейдет в центр? Момент инерции человека рассчитывать как для материальной точки. Какую работу совершит при этом человек.
будет совершать платформа, если человек перейдет в центр? Момент инерции человека рассчитывать как для материальной точки. Какую работу совершит при этом человек.
Решение. Так как платформа вращается по инерции, то результирующий момент всех внешних сил, приложенных к системе платформа-человек, равен нулю. Следовательно, выполняется закон сохранения момента импульса:
 ,
, 
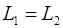 . (1)
. (1)
Когда человек стоит на краю платформы, момент импульса системы платформа-человек равен
 , (2)
, (2)
где 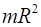 – момент инерции человека;
– момент инерции человека;  – момент инерции системы,
– момент инерции системы,  – угловая скорость платформы.
– угловая скорость платформы.
Когда человек стоит в центре платформы, момент импульса системы равен
 , (3)
, (3)
где 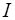 и
и  – момент инерции и угловая скорость системы. Здесь учтено, что момент инерции человека, стоящего в центре платформы, равен нулю. Решая совместно уравнения (1) – (3) получаем
– момент инерции и угловая скорость системы. Здесь учтено, что момент инерции человека, стоящего в центре платформы, равен нулю. Решая совместно уравнения (1) – (3) получаем
 .
.
Из закона сохранения энергии определим работу, совершенную человеком, как изменение механической энергии системы:
 .
.
Задача 8. Найти момент инерции 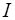 тонкого кольца массы
тонкого кольца массы  и радиуса
и радиуса  относительно оси, лежащей в плоскости кольца и проходящей через его центр (рис. 2.17).
относительно оси, лежащей в плоскости кольца и проходящей через его центр (рис. 2.17).
Решение. Разобьем кольцо на элементы массой  ,
,
где  – линейная плотность;
– линейная плотность;  – длина дуги.
– длина дуги.  – расстояние от элемента
– расстояние от элемента 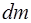 до оси вращения.
до оси вращения.

Рис. 2.17

 ,
,  – момент инерции тонкого кольца.
– момент инерции тонкого кольца.
Задача 9. Найти момент инерции тонкого диска массы  и радиуса
и радиуса  относительно оси, лежащей в плоскости диска и проходящей через его центр (рис. 2.18).
относительно оси, лежащей в плоскости диска и проходящей через его центр (рис. 2.18).
|
|
|

Рис. 2.18
Решение. Разобьем диск на тонкие кольца радиусом  , толщиной
, толщиной  и массой
и массой
 ,
,
где  – площадь диска;
– площадь диска;  – площадь кольца.
– площадь кольца.
Тогда момент инерции такого кольца, учитывая результат полученный в задаче 8, равен
 .
.
Интегрируя по  от
от  до радиуса диска
до радиуса диска  , получим момент инерции диска:
, получим момент инерции диска:
 .
.
3.Механические колебания
Колебания – движения, повторяющиеся во времени.
Периодические колебания – движения, повторяющиеся через равные промежутки времени:  , где
, где 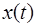 – смещение колеблющейся частицы от положения равновесия, Т – период колебаний,
– смещение колеблющейся частицы от положения равновесия, Т – период колебаний,  – частота колебаний.
– частота колебаний.
Гармонические колебания – это колебания, происходящие по синусоидальному или косинусоидальному закону:
 , (3.1)
, (3.1)
где А – амплитуда колебаний: максимальное смещение частицы из положения равновесия,  – фаза колебаний,
– фаза колебаний,  – начальная фаза (при t =0),
– начальная фаза (при t =0), 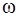 – циклическая частота колебаний
– циклическая частота колебаний
 . (3.2)
. (3.2)
Амплитуда А и частота 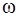 гармонических колебаний постоянны.
гармонических колебаний постоянны.
Гармонический осциллятор – система, совершающая гармонические колебания.
Условие возникновения гармонических колебаний: на частицу (или систему частиц) должна действовать сила или момент сил, пропорциональные смещению частицы из положения равновесия и стремящиеся вернуть ее в положение равновесия.
Такая сила называется квазиупругой и имеет вид
 , (3.3)
, (3.3)
где 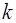 – постоянный коэффициент, называемый квазижесткостью.
– постоянный коэффициент, называемый квазижесткостью.
Пример гармонического осциллятора – шарик на упругой пружинке. Упругая сила, вызывающая колебания пружинного маятника (рис.3.1), имеет вид:
 , (3.4)
, (3.4)
где 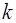 – коэффициент жесткости пружины, х – смещение шарика из положения равновесия.
– коэффициент жесткости пружины, х – смещение шарика из положения равновесия.

Рис.3.1. Горизонтальные колебания грузика на невесомой пружине жесткости k. m – масса грузика
Второй закон Ньютона для шарика, совершающего колебания под действием силы упругости имеет вид
 ,
,  . (3.5)
. (3.5)
Обозначив 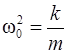 , где
, где  – собственная частота гармонических колебаний, получим динамическое уравнение гармонических колебаний
– собственная частота гармонических колебаний, получим динамическое уравнение гармонических колебаний
 . (3.6)
. (3.6)
Решением уравнения (3.6) является функция
|
|
|
 . (3.7)
. (3.7)
Динамические уравнения движения для систем, совершающих гармонические колебания, затухающие и вынужденные колебания, решения этих уравнений, а так же основные характеристики этих видов колебаний представлены в таблицах 2.2, 2.3 и 2.4.
Физический маятник – это любое физическое тело, совершающее колебания под действием квазиупругого момента силы тяжести  относительно горизонтальной оси Z, не проходящей через центр масс тела (рис.3.2).
относительно горизонтальной оси Z, не проходящей через центр масс тела (рис.3.2).

| Рис. 3.2. Физический маятник. С – центр масс тела. Маятник совершает колебания относительно горизонтальной оси, проходящей через точку О.  – угол отклонения от положения равновесия. l – расстояние от точки подвеса до центра масс тела – угол отклонения от положения равновесия. l – расстояние от точки подвеса до центра масс тела
|
Квазиупругий момент силы тяжести в проекции на ось Z, возвращающий тело (маятник) в положение равновесия, пропорционален углу отклонения  (при малых колебаниях можно считать, что
(при малых колебаниях можно считать, что  )
)
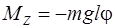 . (3.8)
. (3.8)
Основное уравнение вращательного движения для такого маятника имеет вид
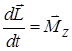 . (3.9)
. (3.9)
В проекции на ось вращения Z
 , (3.10)
, (3.10)
 ,
,
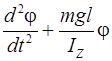 . (3.11)
. (3.11)
Обозначив  , где
, где  – собственная частота колебаний физического маятника, получим
– собственная частота колебаний физического маятника, получим
 . (3.12)
. (3.12)
Решением уравнения (3.12) является функция
 . (3.13)
. (3.13)
Период колебаний физического маятника
 . (3.14)
. (3.14)
Математический маятник – это материальная точка массы  , подвешенная на нерастяжимой нити длинной
, подвешенная на нерастяжимой нити длинной 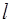 , совершающая колебания в вертикальной плоскости (рис.3.3).
, совершающая колебания в вертикальной плоскости (рис.3.3).
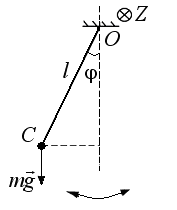
Рис.3.3 Математический маятник. l – длина нити маятника
Момент инерции материальной точки  . Период малых колебаний математического маятника:
. Период малых колебаний математического маятника:
 . (3.15)
. (3.15)
Циклическая частота колебаний 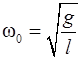 . (3.16)
. (3.16)
Таблица 2.2. Гармонические колебания
| Силы, действующие на частицу | Консервативная квазиупругая сила  ,
где ,
где  – смещение от положения равновесия – смещение от положения равновесия
|
| Второй закон Ньютона | 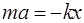 , , 
|
| Динамическое уравнение |  , где , где  – собственная частота гармонических колебаний осциллятора – собственная частота гармонических колебаний осциллятора
|
| Решение динамического уравнения |  , где , где  – амплитуда колебаний, – амплитуда колебаний,  – фаза колебаний – фаза колебаний
|
| Характеристики колебаний | 
|
| Энергия колебаний | 



 – при вращательном движении – при вращательном движении
|
Таблица 2.3. Затухающие колебания
| Силы, действующие на частицу |  – квазиупругая сила, – квазиупругая сила,
 – сила сопротивления,
где – сила сопротивления,
где  – коэффициент сопротивления – коэффициент сопротивления
| ||
| Второй закон Ньютона |  , , 
| ||
| Динамическое уравнение |  , где , где  – собственная частота колебаний осциллятора; – собственная частота колебаний осциллятора;  – коэффициент затухания – коэффициент затухания
| ||
| Решение динамического уравнения |  , где , где  – амплитуда затухающих колебаний, – амплитуда затухающих колебаний,  – начальная фаза; – начальная фаза;  – фаза, – фаза, 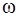 – частота затухающих колебаний – частота затухающих колебаний
| ||
| Характеристики колебаний | 
 – логарифмический декремент затухания, – логарифмический декремент затухания,
|  – частота затухающих колебаний, – частота затухающих колебаний,
 – период затухающих колебаний, – период затухающих колебаний,
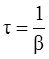 – время релаксации, – время релаксации,
 – добротность осциллятора – добротность осциллятора
| |
| Энергия колебаний | 
| 
 – изменение энергии равно работе сил сопротивления – изменение энергии равно работе сил сопротивления
| |
Таблица 2.4. Вынужденные колебания
|
|
|
|
|
|


