 |
Средние скорости молекул идеального газа. 7 глава
|
|
|
|
На участке 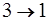 газ изобарически сжимается и отдает количество теплоты
газ изобарически сжимается и отдает количество теплоты 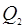 равное
равное
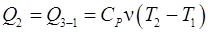 , (6)
, (6)
где 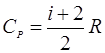 - молярная теплоемкость газа при изобарическом процессе.
- молярная теплоемкость газа при изобарическом процессе.
Подставив значения  и
и 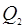 в формулу для к.п.д. цикла:
в формулу для к.п.д. цикла:
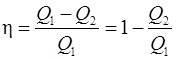 ,
,
получим
 (7)
(7)
Отношение объемов 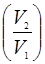 в выражении (7) заменим, согласно закону Гей-Люссака, отношением температур
в выражении (7) заменим, согласно закону Гей-Люссака, отношением температур
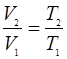 .
.
После подстановки значений 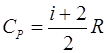 ,
, 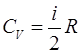 и сокращения на
и сокращения на 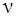 и
и 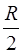 получим
получим
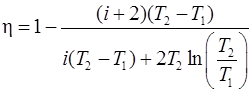 ,
,
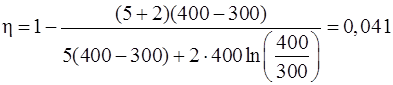 ,
,
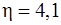 %.
%.
Задача 5. В цилиндре под поршнем находится водород массой 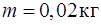 при температуре
при температуре 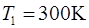 . Водород начал расширяться адиабатно, увеличив свой объем в пять раз, а затем был сжат изотермически, причем объем газа уменьшился в пять раз. Найти температуру
. Водород начал расширяться адиабатно, увеличив свой объем в пять раз, а затем был сжат изотермически, причем объем газа уменьшился в пять раз. Найти температуру 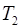 в конце адиабатного расширения и работу
в конце адиабатного расширения и работу  , совершенную газом. Изобразить процесс графически.
, совершенную газом. Изобразить процесс графически.
Решение. Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением
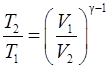 , (1)
, (1)
где 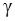 – показатель адиабаты (для водорода, как двухатомного газа,
– показатель адиабаты (для водорода, как двухатомного газа, 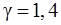 ).
).
Из (1) получаем выражение для конечной температуры 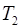 :
:
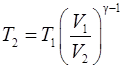 . (2)
. (2)
Подставляя числовые значения заданных величин, находим
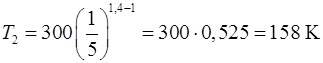 .
.
Работа 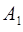 газа при адиабатном расширении определяется по формуле
газа при адиабатном расширении определяется по формуле
 . (3)
. (3)
Подставив в (3) числовые значения величин, получим
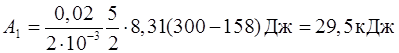 .
.
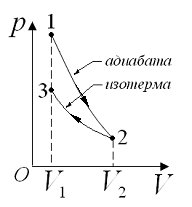 Рис.1.14
Рис.1.14
| Работа 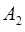 газа при изотермическом сжатии выражается формулой газа при изотермическом сжатии выражается формулой
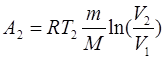 . (4) . (4)
|
Произведя вычисления по формуле (4), найдем  .
.
Знак минус показывает, что при сжатии газа работа совершена внешними силами. Общая работа, совершенная газом при рассмотренных процессах,
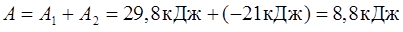 .
.
График процесса приведен на рис.1.14.
Задача 6. Нагреватель тепловой машины, работающей по обратимому циклу Карно, имеет температуру 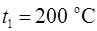 . Определить температуру
. Определить температуру 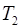 охладителя, если при получении от нагревателя количества теплоты
охладителя, если при получении от нагревателя количества теплоты 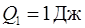 , совершается работа
, совершается работа 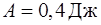 ?
?
Потери на теплоотдачу не учитывать.
|
|
|
Решение. Температуру охладителя 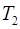 найдем, использовав выражение для термического к.п.д. машины, работающей по циклу
найдем, использовав выражение для термического к.п.д. машины, работающей по циклу
Карно, 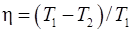 :
:
 . (1)
. (1)
Термический к.п.д. тепловой машины выражает отношение количества теплоты, которое превращено в механическую работу  , к количеству теплоты
, к количеству теплоты 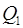 , которое получено рабочим телом тепловой машины из внешней среды (от нагревателя), т. е.
, которое получено рабочим телом тепловой машины из внешней среды (от нагревателя), т. е. 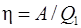 . Подставив это выражение в формулу (1), найдем
. Подставив это выражение в формулу (1), найдем
 . (2)
. (2)
Учтя, что 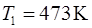 , после вычисления по формуле (2) получим
, после вычисления по формуле (2) получим 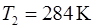 .
.
Задача 7. Найти изменение 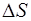 энтропии при нагревании
энтропии при нагревании
воды массой 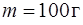 от температуры
от температуры  до температуры
до температуры 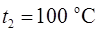 и последующем превращении воды в пар той же температуры.
и последующем превращении воды в пар той же температуры.
Решение. Найдем отдельно изменение энтропии 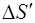 при нагревании воды и изменение энтропии
при нагревании воды и изменение энтропии 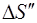 при превращении ее в
при превращении ее в
пар. Полное изменение энтропии выразится суммой 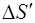 и
и 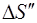 .
.
Изменение энтропии
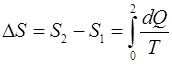 . (1)
. (1)
При бесконечно малом изменении  температуры нагреваемого тела затрачивается количество теплоты
температуры нагреваемого тела затрачивается количество теплоты 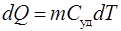 , где
, где  – масса тела;
– масса тела; 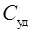 – его удельная теплоемкость. Подставив выражение
– его удельная теплоемкость. Подставив выражение 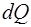 в равенство (1), найдем формулу для вычисления изменения энтропии при нагревании воды:
в равенство (1), найдем формулу для вычисления изменения энтропии при нагревании воды:
 . (2)
. (2)
Вынесем за знак интеграла постоянные величины и произведем интегрирование,
 . (3)
. (3)
После вычислений найдем 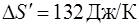 .
.
При вычислении по формуле (1) изменения энтропии во время превращения воды в пар той же температуры постоянная температура 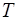 выносится за знак интеграла. Вычислив интеграл, найдем
выносится за знак интеграла. Вычислив интеграл, найдем
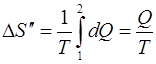 , (4)
, (4)
где  – количество теплоты, переданное при превращении нагретой воды в пар той же температуры.
– количество теплоты, переданное при превращении нагретой воды в пар той же температуры.
Подставив в равенство (4) выражение количества теплоты 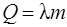 , где
, где 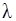 – удельная теплота парообразования, получим
– удельная теплота парообразования, получим
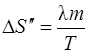 . (5)
. (5)
Произведя вычисления по формуле (5), найдем  .
.
Полное изменение энтропии при нагревании воды и последующем превращении ее в пар
 .
.
Задача 8. Определить изменение 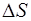 энтропии при изотермическом расширении кислорода массой
энтропии при изотермическом расширении кислорода массой 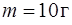 от объема
от объема  до объема
до объема  .
.
Решение. Так как процесс изотермический, то в выражении для энтропии 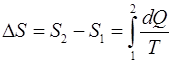 температуру можно вынести за
температуру можно вынести за
знак интеграла:
|
|
|
 . (1)
. (1)
Количество теплоты  , полученное газом, найдем по первому началу термодинамики:
, полученное газом, найдем по первому началу термодинамики: 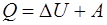 . Для изотермического процесса
. Для изотермического процесса  , следовательно
, следовательно
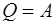 , (2)
, (2)
а работа  изотермического процесса определяется формулой
изотермического процесса определяется формулой
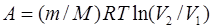 . (3)
. (3)
С учетом (2) и (3) равенство (1) примет вид
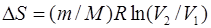 . (4)
. (4)
Подставив в (4) числовые значения и произведя вычисления, получим 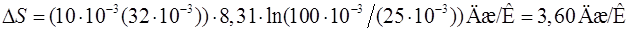
2 Молекулярно-кинетическая теория газов.
Основное уравнение кинетической теории газов
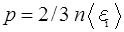 (2.1)
(2.1)
где 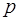 – давление газа;
– давление газа;  – средняя кинетическая энергия поступательно движения молекулы газа,
– средняя кинетическая энергия поступательно движения молекулы газа, 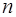 – концентрация.
– концентрация.
Средняя кинетическая энергия:
– приходящаяся на одну степень свободы молекулы
 , (2.2)
, (2.2)
– приходящаяся на все степени свободы молекулы (полная энергия молекулы)
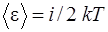 , (2.3)
, (2.3)
– поступательного движения молекулы
 , (2.4)
, (2.4)
где 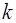 – постоянная Больцмана;
– постоянная Больцмана; 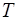 – термодинамическая температура;
– термодинамическая температура;  – число степеней свободы молекулы;
– число степеней свободы молекулы;
– вращательного движения молекулы
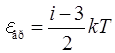 (2.5)
(2.5)
– колебательного движения молекулы
 (2.6)
(2.6)
Зависимость давления газа от концентрации молекул и температуры  .
.
Функция распределения по величине х:
 . (2.7)
. (2.7)
Вероятность того, что значение х находится в пределах 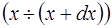 .
.
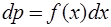 (2.7)
(2.7)
Условие нормировки:
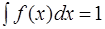 , (2.8)
, (2.8)
где интеграл берется по всем возможным значениям х.
Распределение Гаусса – все случайные величины, соответствующие независимым событиям в природе, подчиняются распределению Гаусса (рис. 2.1):
 , (2.9)
, (2.9)
где  – положительная константа,
– положительная константа, 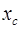 – среднее значение параметра х.
– среднее значение параметра х.
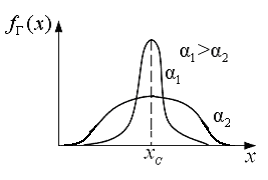
| Рис.2.1. Функция распределения Гаусса, для случайных величин, соответствующих независимым событиям |
Распределение Максвелла.
Распределение Максвелла получено при следующих предположениях:
1. Внешние силовые поля на молекулы газа не действуют.
2. 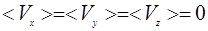 все направления равновероятны.
все направления равновероятны.
3. Независимые проекции скорости 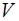 подчиняются распределению Гаусса
подчиняются распределению Гаусса
 (2.10)
(2.10)
где  .
.
Вероятность того, что конкретная молекула имеет проекции скорости в пределах:
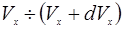 ,
,  ,
,  , равна произведению вероятностей независимых событий
, равна произведению вероятностей независимых событий
 . (2.11)
. (2.11)
Число молекул со скоростями от  до
до 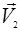
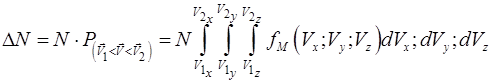 , (2.12)
, (2.12)
где N – общее число молекул.
Функция распределения Максвелла молекул газа по скоростям (в равновесном состоянии) имеет следующий вид
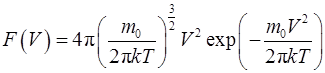 , (2.13)
, (2.13)
где 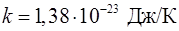 - постоянная Больцмана;
- постоянная Больцмана; 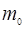 – масса одной молекулы, число Авогадро
– масса одной молекулы, число Авогадро 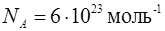 ; универсальная газовая постоянная
; универсальная газовая постоянная 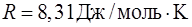 .
.
|
|
|
Относительная доля молекул, обладающих скоростями в диапазоне от 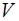 до
до 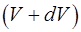 :
:
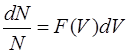 . (2.14)
. (2.14)
Средняя скорость молекул газа.

|
Рис.2.2 Средние скорости молекул газа: 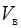 – наиболее вероятная; – наиболее вероятная; 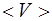 – средняя арифметическая; – средняя арифметическая; 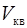 – средняя квадратичная скорость. – средняя квадратичная скорость.
|
Температура идеального газа является мерой кинетической энергии его молекул. В этом заключается смысл термодинамического параметра – температуры в молекулярно – кинетической теории.
Средние скорости молекул идеального газа.
Таблица 2.1
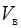 -наиболее вероятная -наиболее вероятная
| соответствует максимуму функции распределения 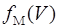

| 
|
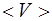 - средняя арифметическая - средняя арифметическая
| 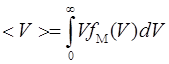

| 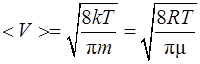
|
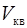 - средняя квадратичная скорость - средняя квадратичная скорость
| соответствует молекулам со средней кинетической энергией
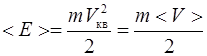
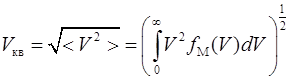
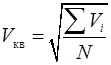
| 
|
Распределение Больцмана (распределение частиц в силовом поле)
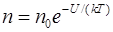 (2.15)
(2.15)
где 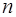 – концентрация частиц;
– концентрация частиц;  – их потенциальная энергия;
– их потенциальная энергия; 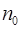 – концентрация частиц в точках поля, где
– концентрация частиц в точках поля, где 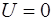 ;
; 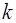 – постоянная Больцмана; Т – термодинамическая температура;
– постоянная Больцмана; Т – термодинамическая температура; 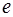 – основание натуральных логарифмов.
– основание натуральных логарифмов.
Барометрическая формула (распределение давления в однородном поле силы тяжести)
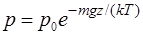 или
или 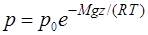 , (2.16)
, (2.16)
где 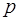 – давление газа,
– давление газа,  – масса частицы,
– масса частицы, 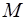 – молярная масса,
– молярная масса, 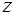 – координата (высота) точки по отношению к уровню, принятому за нулевой,
– координата (высота) точки по отношению к уровню, принятому за нулевой, 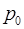 – давление на этом уровне,
– давление на этом уровне, 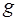 – ускорение свободного падения,
– ускорение свободного падения,  – молярная газовая постоянная.
– молярная газовая постоянная.
Среднее значение физической величины  в общем случае
в общем случае
 , (2.17)
, (2.17)
а в том случае, если функция распределения нормирована на единицу
 , (2.18)
, (2.18)
где  – функция распределения, а интегрирование ведется по всем значениям величины
– функция распределения, а интегрирование ведется по всем значениям величины  .
.
Например, среднее значение скорости молекулы (т.е. средняя арифметическая скорость)  ; средняя квадратичная скорость
; средняя квадратичная скорость 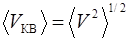 , где
, где 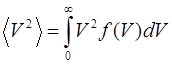 ; средняя кинетическая энергия поступательного движения молекулы
; средняя кинетическая энергия поступательного движения молекулы 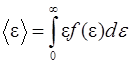 .
.
Среднее число соударений, испытываемых одной молекулой газа в единицу времени,
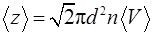 , (2.19)
, (2.19)
где 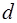 – эффективный диаметр молекулы;
– эффективный диаметр молекулы; 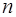 – концентрация молекул,
– концентрация молекул, 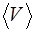 – средняя арифметическая скорость молекул.
– средняя арифметическая скорость молекул.
Средняя длина свободного пробега молекул газа
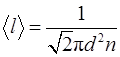 . (2.20)
. (2.20)
Импульс (количество движения), переносимый молекулами из одного слоя газа в другой через элемент поверхности,
|
|
|
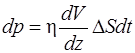 , (2.21)
, (2.21)
где  – динамическая вязкость газа;
– динамическая вязкость газа; 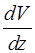 – градиент (поперечный) скорости течения его слоев;
– градиент (поперечный) скорости течения его слоев; 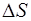 – площадь элемента поверхности,
– площадь элемента поверхности, 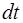 – время переноса.
– время переноса.
Динамическая вязкость
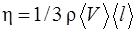 , (2.22)
, (2.22)
где  – плотность газа (жидкости);
– плотность газа (жидкости); 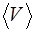 – средняя скорость хаотического движения его молекул;
– средняя скорость хаотического движения его молекул; 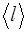 – средняя длина свободного пробега молекул газа.
– средняя длина свободного пробега молекул газа.
Задача 1. В колбе вместимостью 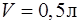 находится кислород при нормальных условиях. Определить среднюю энергию
находится кислород при нормальных условиях. Определить среднюю энергию 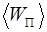 поступательного движения всех молекул, содержащихся в колбе.
поступательного движения всех молекул, содержащихся в колбе.
Решение. Средняя энергия 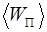 поступательного движения всех молекул может быть выражена соотношением
поступательного движения всех молекул может быть выражена соотношением
 , (1)
, (1)
где 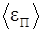 – средняя энергия поступательного движения одной молекулы;
– средняя энергия поступательного движения одной молекулы; 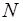 – число всех молекул, содержащихся в колбе.
– число всех молекул, содержащихся в колбе.
Средняя энергия поступательного движения одной молекулы
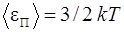 , (2)
, (2)
где 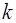 – постоянная Больцмана;
– постоянная Больцмана; 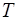 – термодинамическая температура.
– термодинамическая температура.
Число молекул, содержащихся в колбе
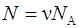 , (3)
, (3)
где 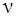 – количество вещества кислорода;
– количество вещества кислорода; 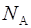 – постоянная Авогадро.
– постоянная Авогадро.
Количество вещества 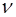 найдем из таких соображений: известно, что при нормальных условиях молярный объем
найдем из таких соображений: известно, что при нормальных условиях молярный объем 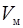 равен
равен  . Так как, по условию задачи, кислород в колбе находится при нормальных условиях, то количество вещества кислорода в колбе выражается соотношением
. Так как, по условию задачи, кислород в колбе находится при нормальных условиях, то количество вещества кислорода в колбе выражается соотношением
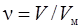 . (4)
. (4)
Подставив (4) в (3), получим
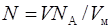 . (5)
. (5)
С учетом (2) и (5) выражение (1) энергии поступательного движения молекул примет вид
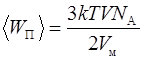 . (6)
. (6)
Подставив значения величин в (6) и произведя вычисления, получим
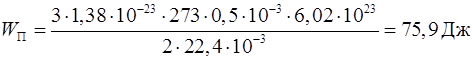 .
.
Задача 2. Найти среднюю кинетическую энергию одной молекулы аммиака 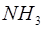 при температуре
при температуре 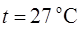 и среднюю энергию вращательного движения этой молекулы при той же температуре.
и среднюю энергию вращательного движения этой молекулы при той же температуре.
Решение. Средняя полная энергия молекулы определяется по формуле
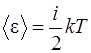 , (1)
, (1)
Число степеней свободы  четырехатомной молекулы, какой является молекула аммиака, равно 6.
четырехатомной молекулы, какой является молекула аммиака, равно 6.
Подставим значения величин в (1):
 .
.
Средняя энергия вращательного движения молекулы определяется по формуле
 , (2)
, (2)
где число 3 означает число степеней свободы поступательного движения.
Подставив в (2) значения величин, получим
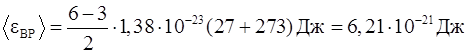 .
.
Заметим, что энергию вращательного движения молекул аммиака можно было получить иначе, разделив полную энергию 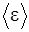 на две равные части. Дело в том, что у трех (и более) атомных молекул число степеней свободы, приходящихся на поступательное и вращательное движение, одинаково (по 3), поэтому энергии поступательного и вращательного движений одинаковы.
на две равные части. Дело в том, что у трех (и более) атомных молекул число степеней свободы, приходящихся на поступательное и вращательное движение, одинаково (по 3), поэтому энергии поступательного и вращательного движений одинаковы.
Задача 3. Какая часть молекул водорода, находящегося при температуре 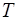 , обладает скоростями, отличающимися от наиболее вероятной скорости не больше чем на 5,0 м/с? Задачу решить для двух значений
, обладает скоростями, отличающимися от наиболее вероятной скорости не больше чем на 5,0 м/с? Задачу решить для двух значений 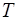 : 1) 400 К, 2) 900 К.
: 1) 400 К, 2) 900 К.
|
|
|
Решение. Распределение молекул по скоростям выражается уравнением
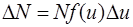 , (1)
, (1)
которое справедливо при условии 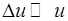 . Поскольку в задаче идёт речь о наиболее вероятной скорости, надо считать
. Поскольку в задаче идёт речь о наиболее вероятной скорости, надо считать 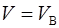 . Следовательно,
. Следовательно,  и уравнение (1) примет вид:
и уравнение (1) примет вид:
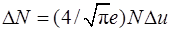 .
.
Отсюда найдем ту часть молекул, относительные скорости которых
лежат в интервале 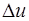 :
:
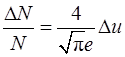 . (2)
. (2)
Прежде чем производить расчеты по (2), необходимо убедиться в том, что выполняется условие 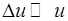 . Так как
. Так как 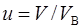 , то
, то
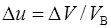 . (3)
. (3)
Чтобы вычислить 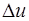 по (3), найдем сначала наиболее вероятную скорость
по (3), найдем сначала наиболее вероятную скорость 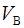 по формуле
по формуле 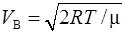 при
при 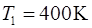 и
и  соответственно:
соответственно:
|
|
|


