 |
Средние скорости молекул идеального газа. 2 глава
|
|
|
|
Системы отсчета, относительно которых тело при отсутствии внешних воздействий движется прямолинейно и равномерно или находится в состоянии покоя, называются инерциальными системами отсчета(ИСО).
Систему отсчета, связанную с Землей, считают ИСО с точностью до вращения Земли относительно своей оси – это первое приближение. Если пренебречь вращением Земли нельзя, то в качестве следующего, второго, более точного приближения к ИСО выбирают систему отсчета, связанную с центром Солнца (гелиоцентрическую систему отсчета).
Импульс частицы 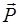 – это вектор, равный произведению массы частицы на ее скорость
– это вектор, равный произведению массы частицы на ее скорость
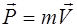 . (2.1)
. (2.1)
Второй закон Ньютона:
Скорость изменения импульса частицы в инерциальной системе отсчета равна векторной сумме сил, действующих на частицу,
 . (2.2)
. (2.2)
Если масса частицы не изменяется во время движения, то
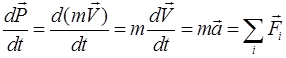 . (2.3)
. (2.3)
В случае переменной массы 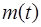 связь между силой, массой и ускорением описывается уравнением Мещерского (реактивное движение):
связь между силой, массой и ускорением описывается уравнением Мещерского (реактивное движение):
 . (2.4)
. (2.4)
Уравнение (2.4) описывает движение любого тела переменной массы в поле внешних сил 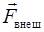 ;
; 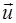 – скорость присоединяющейся (отделяющейся) массы относительно тела;
– скорость присоединяющейся (отделяющейся) массы относительно тела; 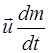 – реактивная сила.
– реактивная сила.
Сила  , действующая на материальную точку, движущуюся по кривой, может быть разложена на две составляющие: тангенциальную
, действующая на материальную точку, движущуюся по кривой, может быть разложена на две составляющие: тангенциальную 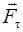 и нормальную
и нормальную 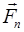 (рис. 2.1):
(рис. 2.1):
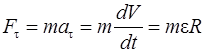 , (2.5)
, (2.5)
где  – угловое ускорение,
– угловое ускорение,  – радиус кривизны траектории;
– радиус кривизны траектории;
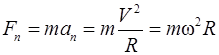 , (2.6)
, (2.6)
где 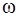 – угловая скорость.
– угловая скорость.

Рис. 2.1. Разложение силы  на тангенциальную
на тангенциальную 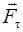 и нормальную
и нормальную 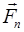 составляющие.
составляющие. 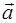 ,
, 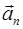 ,
, 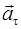 – соответственно полное, нормальное и тангенциальное ускорения.
– соответственно полное, нормальное и тангенциальное ускорения.  – радиус кривизны траектории
– радиус кривизны траектории
Третий закон Ньютона: силы  и
и  взаимодействия двух материальных точек 1 и 2 равны по величине, противоположны по направлению и лежат на прямой, соединяющей эти точки (рис. 2.2):
взаимодействия двух материальных точек 1 и 2 равны по величине, противоположны по направлению и лежат на прямой, соединяющей эти точки (рис. 2.2):
|
|
|
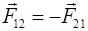 (2.7)
(2.7)
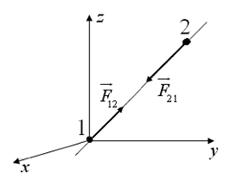
Рис. 2.2. К третьему закону Ньютона
Гравитационная сила. Закон всемирного тяготения
Сила гравитационного притяжения 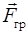 , действующая между материальными точками в соответствии с законом всемирного тяготения, пропорциональна произведению масс взаимодействующих частиц
, действующая между материальными точками в соответствии с законом всемирного тяготения, пропорциональна произведению масс взаимодействующих частиц 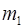 и
и 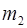 , обратно пропорциональна квадрату расстояния
, обратно пропорциональна квадрату расстояния 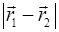 между ними и направлена по прямой, соединяющей эти точки (рис. 2.3).
между ними и направлена по прямой, соединяющей эти точки (рис. 2.3).
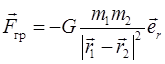 , (2.8)
, (2.8)
 ,
,
где 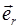 – единичный вектор, направленный вдоль линии, соединяющей частицы,
– единичный вектор, направленный вдоль линии, соединяющей частицы, 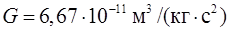 – гравитационная постоянная,
– гравитационная постоянная,
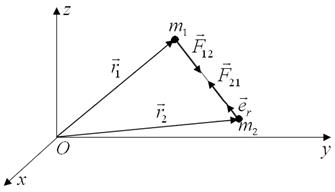
Рис. 2.3. Силы гравитационного взаимодействия  и
и  между двумя материальными точками.
между двумя материальными точками. 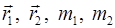 – радиус-векторы и массы взаимодействующих частиц
– радиус-векторы и массы взаимодействующих частиц
Если одну частицу поместить в начало координат (точка 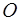 ), то закон примет вид
), то закон примет вид
 ,
, 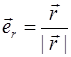 . (2.9)
. (2.9)
Гравитационная сила притяжения частицы планетой

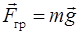 ,
,  , (2.10)
, (2.10)
где 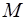 – масса планеты,
– масса планеты,  – масса частицы,
– масса частицы,  – ускорение свободного падения.
– ускорение свободного падения.
Вес – это вертикальная сила, с которой тело действует на опору или подвес. Если тело находится в состоянии равновесия, то она равна по величине силе нормальной реакции опоры 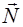 .
.
Сила упругости
Сила упругой деформации при растяжении (сжатии) пружины или стержня определяется законом Гука:
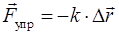 . (2.11)
. (2.11)
В проекции на ось 
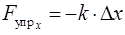 .
. 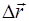 или
или 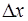 – смещение точки приложения силы
– смещение точки приложения силы  относительно положения равновесия (рис. 2.4). Коэффициент жесткости
относительно положения равновесия (рис. 2.4). Коэффициент жесткости 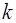 определяется формулой
определяется формулой
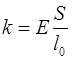 , (2.12)
, (2.12)
где 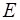 – модуль Юнга или модуль упругости, который характеризует упругие свойства материала стержня,
– модуль Юнга или модуль упругости, который характеризует упругие свойства материала стержня,  – длина недеформированного стержня,
– длина недеформированного стержня, 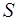 – площадь поперечного сечения стержня.
– площадь поперечного сечения стержня.
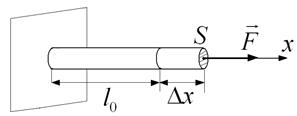
Рис. 2.4. К определению силы упругой деформации 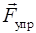 по закону Гука.
по закону Гука.  – сила, растягивающая стержень вдоль оси
– сила, растягивающая стержень вдоль оси  ,
, 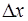 – абсолютное удлинение стержня
– абсолютное удлинение стержня
Закон Гука справедлив только при малых деформациях:
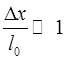 .
.
Силы трения.
Сила трения покоя направлена противоположно внешней силе, зависит от величины внешней силы 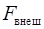 и может иметь величину от нуля до некоторого максимального значения
и может иметь величину от нуля до некоторого максимального значения 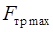 . Если
. Если 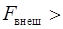
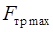 , то тело начинает скользить, и на него уже действует сила трения скольжения:
, то тело начинает скользить, и на него уже действует сила трения скольжения:
|
|
|
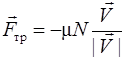 ,
,  . (2.13)
. (2.13)
Здесь 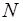 – сила нормальной реакции опоры,
– сила нормальной реакции опоры, 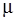 – коэффициент трения скольжения.
– коэффициент трения скольжения.
Сила вязкого трения пропорциональна скорости движения тела и направлена в сторону, противоположную направлению движения,
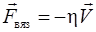 , (2.14)
, (2.14)
где  – коэффициент вязкости среды.
– коэффициент вязкости среды.
Момент импульса частицы относительно начала координат (точка 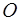 ):
):
 ,
, 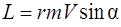 . (2.15)
. (2.15)
По определению 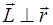 и
и 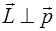 (рис. 2.5). Направление вектора
(рис. 2.5). Направление вектора 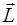 определяется по правилу правого винта (рис. 2.6).
определяется по правилу правого винта (рис. 2.6).
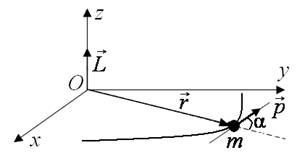
Рис. 2.5. Момент импульса 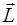 материальной точки массой
материальной точки массой  относительно начала координат (точка
относительно начала координат (точка 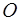 ).
). 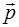 и
и  - импульс и радиус-вектор материальной точки
- импульс и радиус-вектор материальной точки
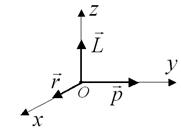
Рис. 2.6. К определению направления момента импульса 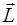 по правилу правого винта
по правилу правого винта
 , (2.16)
, (2.16)
где 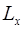 ,
, 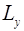 ,
,  – проекции момента импульса частицы на координатные оси.
– проекции момента импульса частицы на координатные оси.
Для частицы, вращающейся по окружности радиуса  (рис. 2.7),
(рис. 2.7),
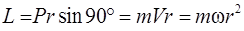 , (2.17)
, (2.17)
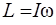 , (2.18)
, (2.18)
где 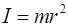 – момент инерции материальной точки.
– момент инерции материальной точки.
Для частицы, движущейся по прямой (рис. 2.8),
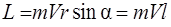 , (2.19)
, (2.19)
где 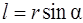 – кратчайшее расстояние от начала координат (точка
– кратчайшее расстояние от начала координат (точка 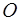 ) до траектории частицы.
) до траектории частицы.
Величина 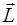 зависит от выбора точки
зависит от выбора точки 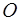 . Если имеется ось вращения, точку
. Если имеется ось вращения, точку 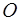 помещают на этой оси.
помещают на этой оси.
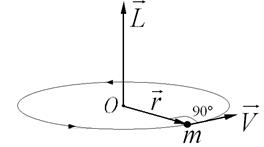
Рис. 2.7. Момент импульса 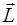 частицы, движущейся по окружности радиуса
частицы, движущейся по окружности радиуса  со скоростью
со скоростью 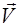 ,
,  – масса частицы
– масса частицы
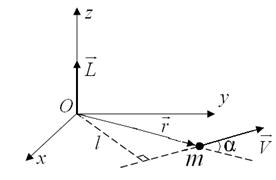
Рис. 2.8. Момент импульса 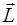 частицы, движущейся по прямолинейной траектории со скоростью
частицы, движущейся по прямолинейной траектории со скоростью 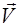 .
.  – радиус-вектор частицы.
– радиус-вектор частицы. 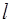 – кратчайшее расстояние от начала координат (точка
– кратчайшее расстояние от начала координат (точка 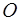 ) до траектории частицы.
) до траектории частицы.  – масса частицы
– масса частицы
Момент силы 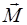 относительно начала координат (точка
относительно начала координат (точка 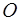 ) равен векторному произведению векторов
) равен векторному произведению векторов  и
и  :
:
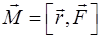 ,
, 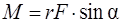 , (2.20)
, (2.20)
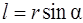 – плечо силы.
– плечо силы.
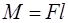 .
.
По определению  и
и 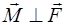 (рис. 2.9). Направление вектора
(рис. 2.9). Направление вектора 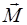 определяется по правилу правого винта (рис. 2.10).
определяется по правилу правого винта (рис. 2.10).
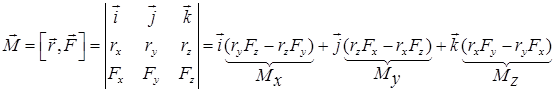 . (2.21)
. (2.21)
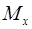 ,
, 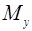 ,
, 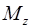 – проекции момента силы на координатные оси. Величина и направление вектора момента силы
– проекции момента силы на координатные оси. Величина и направление вектора момента силы 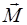 зависят от выбора точки
зависят от выбора точки 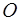 .
.
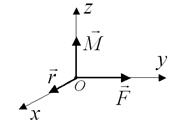
Рис. 2.9. К определению направления момента силы 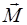 по правилу правого винта
по правилу правого винта
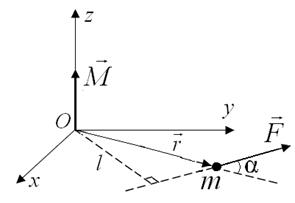
Рис. 2.10. Момент импульса 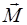 относительно начала координат (точка
относительно начала координат (точка 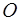 ).
).  – сила, действующая на частицу массой
– сила, действующая на частицу массой  .
. 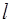 – кратчайшее расстояние от точки
– кратчайшее расстояние от точки 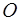 до линии действия силы
до линии действия силы
Основное уравнение динамики вращательного движения
Скорость изменения момента импульса частицы 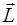 относительно некоторой точки равна моменту силы относительно этой же точки:
относительно некоторой точки равна моменту силы относительно этой же точки:
|
|
|
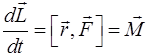 , (2.22)
, (2.22)
 , (2.23)
, (2.23)
где 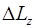 – изменение момента импульса за время
– изменение момента импульса за время 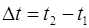 равно импульсу момента силы за это же время.
равно импульсу момента силы за это же время.
Момент инерции материальной точки:
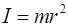 , (2.24)
, (2.24)
где  – расстояние до оси вращения.
– расстояние до оси вращения.
Момент инерции твердого тела, относительно оси, проходящей через центр масс тела, в общем случае:
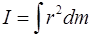 (2.25)
(2.25)
Здесь  – расстояние от элементарной массы
– расстояние от элементарной массы 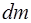 до оси вращения.
до оси вращения.
Моменты инерции некоторых однородных твердых тел относительно оси 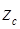 проходящей через центр масс тела, приведены в таблице 2.1.
проходящей через центр масс тела, приведены в таблице 2.1.
Теорема Штейнера: момент инерции тела относительно произвольной оси 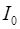 равен сумме момента инерции этого тела относительно оси, параллельной данной и проходящей через центр масс тела
равен сумме момента инерции этого тела относительно оси, параллельной данной и проходящей через центр масс тела 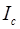 , и произведения массы тела
, и произведения массы тела  на квадрат расстояния между осями
на квадрат расстояния между осями 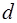 :
:
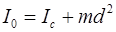 (2.26)
(2.26)
Таблица 2.1
Моменты инерции однородных тел относительно оси, проходящей через центр масс тела
| Твердое тело | ось вращения | Момент инерции 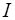
|
Тонкий стержень длины 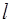
| 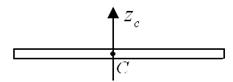 Ось
Ось 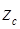 перпендикулярна оси стержня перпендикулярна оси стержня
| 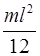
|
Сплошной цилиндр радиуса 
|
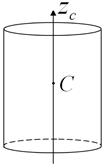 Ось
Ось 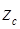 совпадает с осью цилиндра совпадает с осью цилиндра
|

|
Тонкое кольцо радиуса 
| 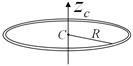 Ось
Ось 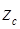 перпендикулярна плоскости кольца перпендикулярна плоскости кольца
|
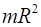
|
Тонкий диск радиуса 
| 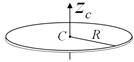 Ось
Ось 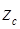 перпендикулярна плоскости диска перпендикулярна плоскости диска
|

|
Тонкий диск радиуса 
|
 Ось
Ось  совпадает с диаметром диска совпадает с диаметром диска
| 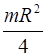
|
Сплошной шар радиуса 
| 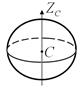 Ось
Ось 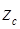 проходит через центр шара проходит через центр шара
|
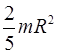
|
Работа силы равна интегралу от скалярного произведения вектора силы на вектор бесконечно малого перемещения
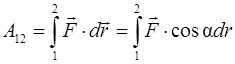 . (2.27)
. (2.27)
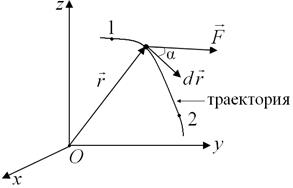
Рис. 2.11. К определению работы силы на участке траектории 1 – 2
Сила совершает положительную работу, когда она направлена «по движению» (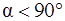 ), отрицательную, когда она направлена «против движения» (
), отрицательную, когда она направлена «против движения» (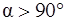 ). Работа силы равна нулю, когда
). Работа силы равна нулю, когда 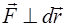 (
(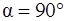 ).
).
Работа момента силы при повороте тела относительно оси 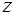 равна изменению кинетической энергии:
равна изменению кинетической энергии:
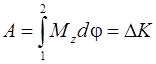 . (2.28)
. (2.28)
Мощность силы равна работе, совершенной за единицу времени:
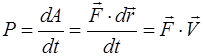 . (2.29)
. (2.29)
Кинетическая энергия:
а) тела, движущегося поступательно,
 , (2.30)
, (2.30)
где 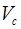 – скорость центра масс тела;
– скорость центра масс тела;
б) тела, вращающегося относительно неподвижной оси 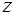 ,
,
|
|
|
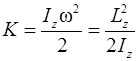 ; (2.31)
; (2.31)
в) тела, совершающего плоское движение,
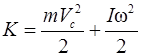 . (2.32)
. (2.32)
Потенциальная энергия:
а) упругодеформированной пружины
 , (2.33)
, (2.33)
где 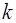 – жесткость пружины,
– жесткость пружины, 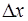 – абсолютная деформация пружины;
– абсолютная деформация пружины;
б) гравитационного взаимодействия
 , (2.34)
, (2.34)
где 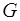 – гравитационная постоянная,
– гравитационная постоянная, 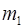 и
и 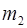 – массы взаимодействующих тел;
– массы взаимодействующих тел;  – расстояние между центрами этих тел;
– расстояние между центрами этих тел;
в) тела, находящегося в однородном поле силы тяжести Земли,
 , (2.35)
, (2.35)
где 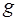 – ускорение свободного падения,
– ускорение свободного падения, 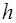 – высота тела над уровнем, принятым за нулевой (формула справедлива при условии
– высота тела над уровнем, принятым за нулевой (формула справедлива при условии 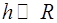 , где
, где  – радиус Земли).
– радиус Земли).
Законы сохранения
Закон сохранения импульса
Импульс замкнутой системы сохраняется: 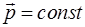 .
.
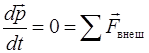
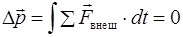 (2.36)
(2.36)
Система называется замкнутой, если все внешние силы, действующие на систему, уравновешены.
Проекция импульса на ось сохраняется, если сумма проекций внешних сил на эту ось равна нулю: 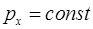 , если
, если 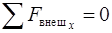 .
.
Если действие внешних сил длится очень малое время 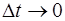 (столкновение, взрыв), то
(столкновение, взрыв), то 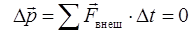 , т.е.
, т.е. 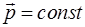 .
.
Для двух взаимодействующих точек закон сохранения импульса имеет вид
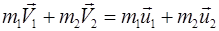 , (2.37)
, (2.37)
где 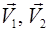 и
и 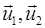 – скорости точек до и после их взаимодействия.
– скорости точек до и после их взаимодействия.
Полная механическая энергия системы частиц, находящихся во внешнем потенциальном поле,
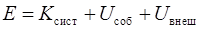 , (2.38)
, (2.38)
где 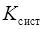 – сумма кинетических энергий всех частиц системы:
– сумма кинетических энергий всех частиц системы:
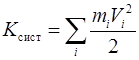 , (2.39)
, (2.39)
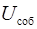 – собственная потенциальная энергия системы частиц:
– собственная потенциальная энергия системы частиц:
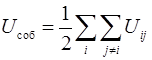 , (2.40)
, (2.40)
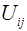 – потенциальная энергия взаимодействия
– потенциальная энергия взаимодействия  -ой и
-ой и 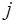 -ой частиц,
-ой частиц,
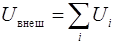 , где
, где 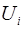 – потенциальная энергия
– потенциальная энергия  -ой частицы во внешнем поле.
-ой частицы во внешнем поле.
Консервативной называется система, полная механическая энергия которой сохраняется 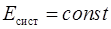 .
.
Закон сохранения момента импульса:
Момент импульса системы сохраняется, если сумма моментов всех внешних сил, действующих на систему, равна нулю.
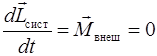 ,
, 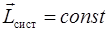 . (2.41)
. (2.41)
Если проекция моментов внешних сил на какую-либо ось равна нулю, то проекция момента импульса на эту ось сохраняется:
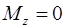 ,
, 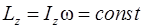 . (2.42)
. (2.42)
Примеры решения задач
Задача 1. Тело массой 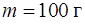 движется так, что зависимость пройденного пути от времени описывается уравнением
движется так, что зависимость пройденного пути от времени описывается уравнением 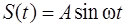 , где
, где 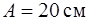 ,
, 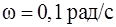 . Запишите закон изменения силы как функцию времени. Определите модуль силы, действующей на тело через
. Запишите закон изменения силы как функцию времени. Определите модуль силы, действующей на тело через 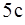 после начала движения.
после начала движения.
|
|
|


