 |
Средние скорости молекул идеального газа. 5 глава
|
|
|
|
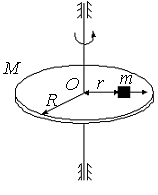
Рис.5
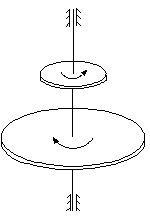
Рис.6
133. Однородный горизонтальный диск радиуса 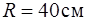 может вращаться вокруг закрепленной вертикальной оси, проходящей через его центр. Первоначально диск покоился. Затем нить, намотанная на обод диска, начинают тянуть с силой
может вращаться вокруг закрепленной вертикальной оси, проходящей через его центр. Первоначально диск покоился. Затем нить, намотанная на обод диска, начинают тянуть с силой 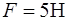 (рис.7). За время
(рис.7). За время 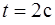 диск повернулся на угол
диск повернулся на угол 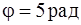 , причем при вращении на него действует постоянный тормозящий момент сил трения
, причем при вращении на него действует постоянный тормозящий момент сил трения  . Какова масса
. Какова масса  диска?
диска?
134. Цилиндр массы  катится по горизонтальной поверхности без проскальзывания. Когда нить, намотанную на цилиндр, тянут горизонтально с силой
катится по горизонтальной поверхности без проскальзывания. Когда нить, намотанную на цилиндр, тянут горизонтально с силой 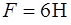 (рис.8). С каким ускорением
(рис.8). С каким ускорением  катится цилиндр?
катится цилиндр?
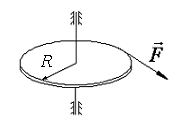
Рис.7
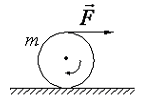
Рис.8
135. В центре горизонтального диска сидел кузнечик массой 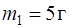 , а на краю диска – другой кузнечик массой
, а на краю диска – другой кузнечик массой  . Диск при этом вращался без трения с некоторой угловой скоростью вокруг закрепленной вертикально оси симметрии (рис.9). Затем кузнечики прыгают навстречу друг другу и меняются местами. Во сколько раз при этом увеличится угловая скорость вращения диска? Масса диска
. Диск при этом вращался без трения с некоторой угловой скоростью вокруг закрепленной вертикально оси симметрии (рис.9). Затем кузнечики прыгают навстречу друг другу и меняются местами. Во сколько раз при этом увеличится угловая скорость вращения диска? Масса диска 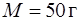 .
.
136. Тонкий стержень массы  и длины
и длины  может вращаться вокруг перпендикулярной ему вертикальной закрепленной оси, проходящей через центр стержня. Первоначально стержень покоился. Затем его начинают тянуть за один из его концов с постоянной силой
может вращаться вокруг перпендикулярной ему вертикальной закрепленной оси, проходящей через центр стержня. Первоначально стержень покоился. Затем его начинают тянуть за один из его концов с постоянной силой 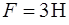 , направленной горизонтально и все время направленной перпендикулярно стержню (рис.10). При вращении на стержень действует постоянный момент сил трения
, направленной горизонтально и все время направленной перпендикулярно стержню (рис.10). При вращении на стержень действует постоянный момент сил трения 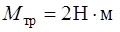 . На какой угол
. На какой угол  повернется стержень за время
повернется стержень за время  ?
?

Рис.9
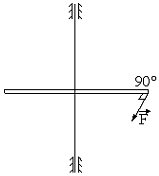
Рис.10
137. Пуля массы 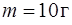 , летевшая горизонтально со скоростью
, летевшая горизонтально со скоростью 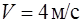 , застряла в нижнем конце тонкого стержня массы
, застряла в нижнем конце тонкого стержня массы  , подвешенного за верхний конец. В результате стержень отклонился на угол
, подвешенного за верхний конец. В результате стержень отклонился на угол 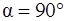 от вертикали. (рис.11). Какова длина стержня?
от вертикали. (рис.11). Какова длина стержня?
138. В тонкий стержень массы 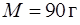 и длины
и длины 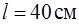 одновременно попадают летевшие горизонтально навстречу друг другу две одинаковые пули массой
одновременно попадают летевшие горизонтально навстречу друг другу две одинаковые пули массой 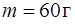 (рис.12). Скорости пуль до удара были одинаковы по величине и равны
(рис.12). Скорости пуль до удара были одинаковы по величине и равны 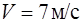 . Первоначально стержень, подвешенный за верхний конец (точка О), висел вертикально. Одна пуля застряла при ударе в нижнем конце стержня, а другая – в его середине. С какой угловой скоростью начнет вращаться стержень сразу после удара?
. Первоначально стержень, подвешенный за верхний конец (точка О), висел вертикально. Одна пуля застряла при ударе в нижнем конце стержня, а другая – в его середине. С какой угловой скоростью начнет вращаться стержень сразу после удара?
|
|
|
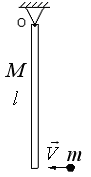
Рис.11
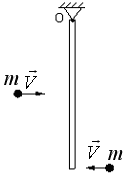
Рис.12
139. Закрепленный за верхний конец тонкий стержень отводят в горизонтальное положение и отпускают без толчка (рис.13). Чему равна скорость нижнего конца стержня в момент прохождения положения равновесия, если длина стержня 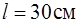 ?
?
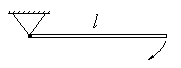
Рис.13
140. Выведите формулу для момента инерции тонкого кольца радиуса  и массой
и массой  относительно оси, проходящей через центр масс кольца и лежащей в плоскости кольца.
относительно оси, проходящей через центр масс кольца и лежащей в плоскости кольца.
141. Выведите формулу для момента инерции тонкого стержня длиной 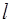 и массой
и массой  относительно оси, проходящей через центр масс стержня перпендикулярно его длине.
относительно оси, проходящей через центр масс стержня перпендикулярно его длине.
142. Выведите формулу для момента инерции тонкого диска радиусом  и массой
и массой  относительно оси, проходящей через центр масс диска и лежащей в плоскости диска.
относительно оси, проходящей через центр масс диска и лежащей в плоскости диска.
143. Выведите формулу для момента инерции сплошного шара радиусом  и массой
и массой  относительно оси, проходящей через центр масс шара.
относительно оси, проходящей через центр масс шара.
144. Выведите формулу для момента инерции полого шара относительно оси, проходящей через центр масс шара. Масса шара равна  , внутренний радиус
, внутренний радиус  , внешний
, внешний  .
.
145. Выведите формулу для момента инерции сплошного цилиндра, относительно оси, совпадающей с его осью симметрии. Масса цилиндра  , радиус
, радиус  .
.
146. Выведите формулу для момента инерции муфты относительно оси, совпадающей с ее осью симметрии (рис.14). Масса муфты  , внутренний радиус
, внутренний радиус  , внешний
, внешний  .
.
147. Выведите формулу для момента инерции тонкого стержня длиной 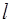 и массой
и массой  относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на
относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на 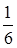 его длины.
его длины.
|
|
|
148. Два одинаковых тонких однородных стержня массой  и длиной
и длиной 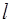 каждый приварили концами перпендикулярно друг к другу (рис.15). Выведите формулу момента инерции получившейся детали относительно оси, проходящей через центр масс одного из стержней (точка С) перпендикулярно плоскости детали.
каждый приварили концами перпендикулярно друг к другу (рис.15). Выведите формулу момента инерции получившейся детали относительно оси, проходящей через центр масс одного из стержней (точка С) перпендикулярно плоскости детали.
 Рис.14
Рис.14
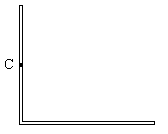
Рис.15
149. Из трех одинаковых тонких однородных стрежней массой  и длиной
и длиной 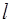 каждый сварили деталь в виде равностороннего треугольника (рис.16). Выведите формулу для момента инерции получившейся детали относительно оси, проходящей через вершину треугольника (точка О) перпендикулярно плоскости детали.
каждый сварили деталь в виде равностороннего треугольника (рис.16). Выведите формулу для момента инерции получившейся детали относительно оси, проходящей через вершину треугольника (точка О) перпендикулярно плоскости детали.
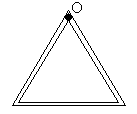
Рис.16
150. Шар массой  двигаясь со скоростью
двигаясь со скоростью 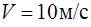 , упруго ударяется о гладкую неподвижную вертикальную стенку. В момент удара вектор его скорости направлен под углом
, упруго ударяется о гладкую неподвижную вертикальную стенку. В момент удара вектор его скорости направлен под углом  к горизонтали. Определите импульс, полученный стенкой.
к горизонтали. Определите импульс, полученный стенкой.
151. Два шара массами 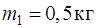 и
и 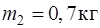 движутся навстречу друг другу со скоростями
движутся навстречу друг другу со скоростями 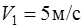 и
и 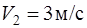 . Определите скорость шаров после прямого, неупругого удара и долю кинетической энергии шаров, превратившуюся во внутреннюю энергию.
. Определите скорость шаров после прямого, неупругого удара и долю кинетической энергии шаров, превратившуюся во внутреннюю энергию.
152. Снаряд, летевший горизонтально на высоте 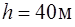 со скоростью
со скоростью  , разрывается на две равные части. Одна часть снаряда через
, разрывается на две равные части. Одна часть снаряда через  падает на Землю точно под местом взрыва. Определить скорость другой части снаряда сразу после взрыва.
падает на Землю точно под местом взрыва. Определить скорость другой части снаряда сразу после взрыва.
153. На горизонтальных рельсах стоит платформа с песком (общая масса 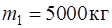 ). В песок попадает снаряд массы
). В песок попадает снаряд массы 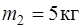 , летевший вдоль рельсов. В момент попадания скорость снаряда
, летевший вдоль рельсов. В момент попадания скорость снаряда 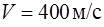 и направлена сверху вниз под углом
и направлена сверху вниз под углом  к горизонту (рис.17). Какую скорость приобретет платформа, если снаряд застревает в песке.
к горизонту (рис.17). Какую скорость приобретет платформа, если снаряд застревает в песке.
154. После абсолютно упругого соударения тела массы  , двигавшегося поступательно, с покоившимся телом массы
, двигавшегося поступательно, с покоившимся телом массы 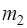 оба тела разлетаются симметрично относительно направления вектора скорости первого тела до удара (рис.18). При каких значениях
оба тела разлетаются симметрично относительно направления вектора скорости первого тела до удара (рис.18). При каких значениях 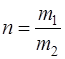 это возможно, если угол
это возможно, если угол  между векторами скоростей тел после удара равен
между векторами скоростей тел после удара равен  ?
?
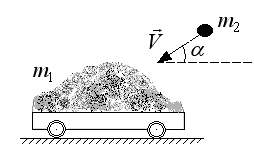
Рис.17
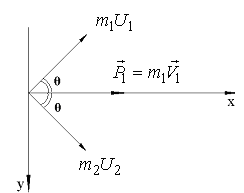
Рис.18
155. Решите задачу 154 для значения 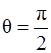 .
.
156. Пуля массы  , летящая горизонтально со скоростью
, летящая горизонтально со скоростью 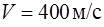 , попадает в мешок, набитый ватой, массы
, попадает в мешок, набитый ватой, массы  , который висит на длинном шнуре. На какую высоту
, который висит на длинном шнуре. На какую высоту 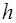 поднимется мешок? Какая доля кинетической энергии пули будет израсходована на пробивание ваты? (рис.19).
поднимется мешок? Какая доля кинетической энергии пули будет израсходована на пробивание ваты? (рис.19).
|
|
|
157. Пуля массы  , летящая горизонтально со скоростью
, летящая горизонтально со скоростью 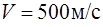 , попадает в диск массы
, попадает в диск массы  , который висит на длинном шнуре. На какую высоту
, который висит на длинном шнуре. На какую высоту 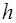 поднимется диск? Удар пули о диск считать абсолютно упругим (рис. 20).
поднимется диск? Удар пули о диск считать абсолютно упругим (рис. 20).
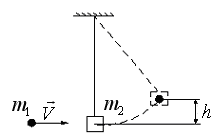
Рис.19
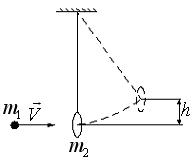
Рис.20
158. Модель ракеты движется при отсутствии внешних сил, выбрасывая непрерывную струю газов с постоянной относительно ракеты скоростью  . (рис. 21). Расход газа
. (рис. 21). Расход газа 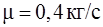 , начальная масса ракеты
, начальная масса ракеты  . Какую скорость относительно Земли приобретет ракета через
. Какую скорость относительно Земли приобретет ракета через  после начала движения, если начальная скорость равна нулю, внешние силы на ракету не действуют.
после начала движения, если начальная скорость равна нулю, внешние силы на ракету не действуют.
159. Два шара массами 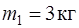 и
и  подвешены на нити длиной
подвешены на нити длиной  . Первоначально шары соприкасаются между собой, затем шар большей массы отклонили от положения равновесия на угол
. Первоначально шары соприкасаются между собой, затем шар большей массы отклонили от положения равновесия на угол  и отпустили. Считая удар упругим, определите скорость второго шара после удара. (рис. 22).
и отпустили. Считая удар упругим, определите скорость второго шара после удара. (рис. 22).
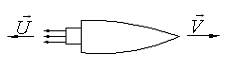
Рис.21
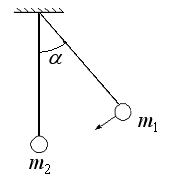
Рис.22
160. Материальная точка движется вдоль оси  так, что ее скорость зависит от координаты
так, что ее скорость зависит от координаты  по закону
по закону 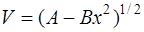 , где
, где 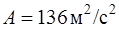 ,
, 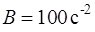 . Показать, что уравнение движения точки является динамическим уравнением гармонических колебаний и найти период этих колебаний.
. Показать, что уравнение движения точки является динамическим уравнением гармонических колебаний и найти период этих колебаний.
161. Тонкий сплошной диск массой 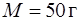 и радиуса
и радиуса  может вращаться без трения вокруг закрепленной горизонтальной оси симметрии (точка О). К краю диска прикрепили маленький грузик массы
может вращаться без трения вокруг закрепленной горизонтальной оси симметрии (точка О). К краю диска прикрепили маленький грузик массы 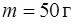 (рис. 23). Найти период малых колебаний такой системы.
(рис. 23). Найти период малых колебаний такой системы.
162. Маятник часов имеет вид массивного диска, закрепленного на практически невесомом тонком стержне длины  , и может колебаться относительно горизонтальной оси (точка О), проходящей через другой конец стержня перпендикулярно плоскости диска (рис. 24). Чему равен радиус диска
, и может колебаться относительно горизонтальной оси (точка О), проходящей через другой конец стержня перпендикулярно плоскости диска (рис. 24). Чему равен радиус диска  , если маятник совершает колебания с периодом
, если маятник совершает колебания с периодом 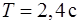 ? Трение отсутствует.
? Трение отсутствует.
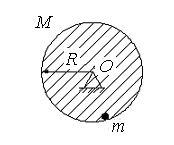
Рис.23

Рис.24
163. Тонкий стержень массы 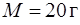 совершает незатухающие колебания под действием силы тяжести вокруг закрепленной горизонтальной оси (точка О), проходящей через его конец. (рис. 25) Во сколько раз возрастет период колебаний стержня, если к другому его концу прикрепить грузик массой
совершает незатухающие колебания под действием силы тяжести вокруг закрепленной горизонтальной оси (точка О), проходящей через его конец. (рис. 25) Во сколько раз возрастет период колебаний стержня, если к другому его концу прикрепить грузик массой  , размерами которого можно пренебречь.
, размерами которого можно пренебречь.
|
|
|
164. Амплитуда незатухающих гармонических колебаний маленького грузика на пружинке 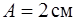 , полная механическая энергия колебаний
, полная механическая энергия колебаний  . При каком смещении
. При каком смещении  от положения равновесия на колеблющийся грузик действует сила
от положения равновесия на колеблющийся грузик действует сила  .
.
165. Тонкий стержень с массой  совершает незатухающие колебания с периодом
совершает незатухающие колебания с периодом  вокруг горизонтальной закрепленной оси (точка О на рис.26), проходящей через его конец. На другом конце стержня сидит жук массой
вокруг горизонтальной закрепленной оси (точка О на рис.26), проходящей через его конец. На другом конце стержня сидит жук массой 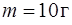 . Чему станет равным период колебаний стержня, когда жук улетит?
. Чему станет равным период колебаний стержня, когда жук улетит?
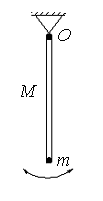
Рис.25
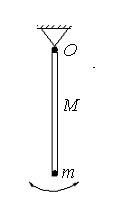
Рис.26
166. На каком расстоянии  от края тонкого стержня длины
от края тонкого стержня длины  надо закрепить горизонтальную ось вращения (точка О), чтобы стержень совершал колебания под действием силы тяжести с тем же периодом, что и относительно горизонтальной оси
надо закрепить горизонтальную ось вращения (точка О), чтобы стержень совершал колебания под действием силы тяжести с тем же периодом, что и относительно горизонтальной оси 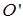 , проходящей через его край (рис. 27)? Трением в осях пренебречь.
, проходящей через его край (рис. 27)? Трением в осях пренебречь.
167. Тонкий однородный стержень длины 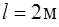 массы
массы  совершает гармонические незатухающие колебания под действием силы тяжести относительно горизонтальной оси, перпендикулярной стержню и проходящей через его конец. В положении равновесия стержень имеет угловую скорость
совершает гармонические незатухающие колебания под действием силы тяжести относительно горизонтальной оси, перпендикулярной стержню и проходящей через его конец. В положении равновесия стержень имеет угловую скорость 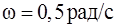 . Найдите максимальный угол, на который отклоняется стержень в процессе движения.
. Найдите максимальный угол, на который отклоняется стержень в процессе движения.
168. Грузик массой  прикреплен к пружине жесткости
прикреплен к пружине жесткости  и совершает незатухающие гармонические колебания в горизонтальной плоскости с амплитудой
и совершает незатухающие гармонические колебания в горизонтальной плоскости с амплитудой 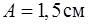 . В начальный момент грузик вышел из положения равновесия. За какое время он пройдет путь, равный половине амплитуды?
. В начальный момент грузик вышел из положения равновесия. За какое время он пройдет путь, равный половине амплитуды?
169. Тонкий однородный стержень массы 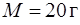 и длины
и длины 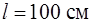 подвешен на горизонтальной оси, проходящей перпендикулярно стержню через его конец. К центру стержня прикреплен шарик массой
подвешен на горизонтальной оси, проходящей перпендикулярно стержню через его конец. К центру стержня прикреплен шарик массой 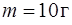 . (рис.28) Найдите период и частоту малых колебаний такого маятника. Трением в оси и размерами шарика можно пренебречь.
. (рис.28) Найдите период и частоту малых колебаний такого маятника. Трением в оси и размерами шарика можно пренебречь.
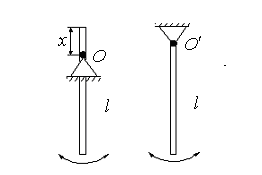
Рис.27
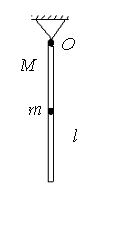
Рис. 28
170.Тонкий стержень, подвешенный за верхний конец, совершает гармонические колебания под действием силы тяжести с периодом 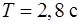 (рис.29). Из-за трения в оси (точка О) эти колебания быстро затухают. Логарифмический декремент затухания равен
(рис.29). Из-за трения в оси (точка О) эти колебания быстро затухают. Логарифмический декремент затухания равен  . Определить длину стержня.
. Определить длину стержня.
171. Тонкий стержень массой  и длиной
и длиной  раскачивается по действием момента сил тяжести и внешнего вынуждающего момента сил
раскачивается по действием момента сил тяжести и внешнего вынуждающего момента сил 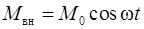 , где
, где  , вокруг закрепленной горизонтальной оси (точка О), проходящей через край стержня. (рис.30) Найти амплитуду
, вокруг закрепленной горизонтальной оси (точка О), проходящей через край стержня. (рис.30) Найти амплитуду  установившихся вынужденных колебаний стержня (в радианах), пренебрегая моментами диссипативных сил трения.
установившихся вынужденных колебаний стержня (в радианах), пренебрегая моментами диссипативных сил трения.
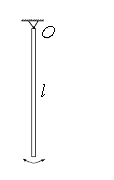
Рис.29
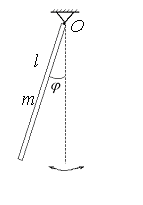
Рис.30
172. Грузик на пружинке жесткости 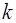 колеблется в жидкости, причем частота его колебаний
колеблется в жидкости, причем частота его колебаний 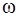 в два раза меньше собственной частоты
в два раза меньше собственной частоты  незатухающих колебаний грузика на той же пружинке. Коэффициент жесткости пружинки
незатухающих колебаний грузика на той же пружинке. Коэффициент жесткости пружинки 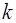 увеличили в 7 раз. Во сколько раз надо увеличить коэффициент вязкого трения жидкости, чтобы период колебаний грузика не изменился (рис.31)?
увеличили в 7 раз. Во сколько раз надо увеличить коэффициент вязкого трения жидкости, чтобы период колебаний грузика не изменился (рис.31)?
|
|
|
173. Тонкий стержень длины  и массы
и массы  может вращаться вокруг горизонтальной оси О, проходящей через его край, причем при вращении в оси возникает тормозящий момент сил, пропорциональный угловой скорости
может вращаться вокруг горизонтальной оси О, проходящей через его край, причем при вращении в оси возникает тормозящий момент сил, пропорциональный угловой скорости 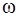 вращения стержня:
вращения стержня: 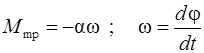 . (рис. 32) Чему должна быть равна постоянная
. (рис. 32) Чему должна быть равна постоянная  , чтобы под действием силы тяжести этот стержень совершал колебания с периодом
, чтобы под действием силы тяжести этот стержень совершал колебания с периодом 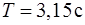 ?
?
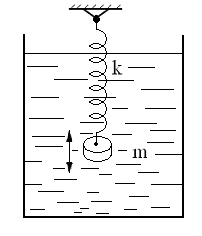
Рис.31
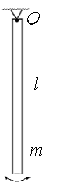
Рис.32
174. Под действием внешней гармонической вынуждающей силы грузик массы 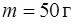 совершает вертикальные вынужденные колебания на пружинке жесткости
совершает вертикальные вынужденные колебания на пружинке жесткости  с частотой
с частотой  и с амплитудой
и с амплитудой 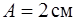 (рис.33). Найти амплитуду
(рис.33). Найти амплитуду 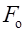 вынуждающей силы. Диссипативные силы трения отсутствуют.
вынуждающей силы. Диссипативные силы трения отсутствуют.
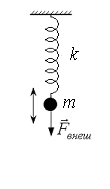
Рис.33
175. Небольшой груз массы 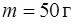 подвешен на пружине и колеблется вертикально в вязкой жидкости с периодом
подвешен на пружине и колеблется вертикально в вязкой жидкости с периодом  . При этом логарифм отношения амплитуды колебаний в некоторый момент времени к амплитуде через период равен
. При этом логарифм отношения амплитуды колебаний в некоторый момент времени к амплитуде через период равен  . Определите коэффициент жесткости пружины
. Определите коэффициент жесткости пружины 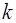 .
.
176. Маленький грузик с массой 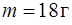 совершает на пружинке с жесткостью
совершает на пружинке с жесткостью 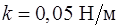 вертикальные колебания в вязкой жидкости, причем амплитуда колебаний уменьшается за время
вертикальные колебания в вязкой жидкости, причем амплитуда колебаний уменьшается за время 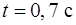 в 2,72 раз. Найти период
в 2,72 раз. Найти период 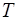 колебаний.
колебаний.
177.На пружине подвешена чашка весов с гирями. При этом период вертикальных колебаний  . После того, как на чашку весов положили еще одну добавочную гирю, пружина удлинилась на
. После того, как на чашку весов положили еще одну добавочную гирю, пружина удлинилась на 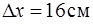 . Каким стал после этого новый период
. Каким стал после этого новый период 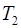 вертикальных колебаний системы?
вертикальных колебаний системы?
178.Внешняя вынуждающая гармоническая сила  , где
, где 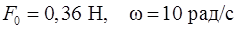 заставляет грузик массы
заставляет грузик массы 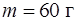 на пружинке совершать вынужденные вертикальные колебания (рис.34). Какова амплитуда А этих вынужденных колебаний, если диссипативные силы трения отсутствуют, а собственная частота
на пружинке совершать вынужденные вертикальные колебания (рис.34). Какова амплитуда А этих вынужденных колебаний, если диссипативные силы трения отсутствуют, а собственная частота  незатухающих колебаний грузика на пружинке в 2 раза больше частоты вынуждающей силы.
незатухающих колебаний грузика на пружинке в 2 раза больше частоты вынуждающей силы.
179.Внешняя гармоническая сила с амплитудой  заставляет грузик массы
заставляет грузик массы 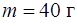 на пружине с жесткостью
на пружине с жесткостью  совершать вынужденные вертикальные колебания с амплитудой
совершать вынужденные вертикальные колебания с амплитудой 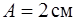 (рис. 35). Диссипативные силы трения отсутствуют. Чему равна частота
(рис. 35). Диссипативные силы трения отсутствуют. Чему равна частота  внешней вынуждающей силы.
внешней вынуждающей силы.

Рис.34
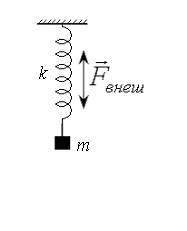
Рис.35
Контрольная работа №2.
Молекулярная физика и термодинамика.
Основные формулы и примеры решения задач.
1. Молекулярное строение вещества.
Законы идеальных газов. Термодинамика.
Количество вещества 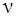 – число структурных элементов
– число структурных элементов 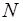 (молекул, атомов), содержащихся в системе или теле. Количество вещества выражается в молях. Моль – количество вещества, содержащее столько же частиц, сколько содержится атомов в 0,012 кг (12 г) углерода
(молекул, атомов), содержащихся в системе или теле. Количество вещества выражается в молях. Моль – количество вещества, содержащее столько же частиц, сколько содержится атомов в 0,012 кг (12 г) углерода 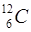 . Один моль любого вещества содержит одно и то же число частиц равное числу Авогадро
. Один моль любого вещества содержит одно и то же число частиц равное числу Авогадро 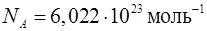 .
.
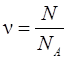 (1.1)
(1.1)
Молярная масса (масса одного моля вещества) – количество вещества, масса которого в граммах численно равна массе частицы в а.е.м. (атомная единица массы), для элемента – это  .
.
 (1.2)
(1.2)
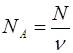 ;
; 
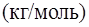 или (1.3)
или (1.3)
|
|
|


