 |
Средние скорости молекул идеального газа. 4 глава
|
|
|
|
| Силы, действующие на частицу |  – квазиупругая сила, – квазиупругая сила,
 – сила сопротивления, – сила сопротивления,
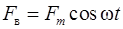 – внешняя сила, где – внешняя сила, где  – амплитудное значение этой силы, – амплитудное значение этой силы, 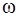 – частота вынуждающей силы – частота вынуждающей силы
| ||
| Второй закон Ньютона |  
| ||
| Динамическое уравнение |  ,
где ,
где  – собственная частота колебаний осциллятора; – собственная частота колебаний осциллятора;  – коэффициент затухания – коэффициент затухания
| ||
| Решение динамического уравнения |  ,
где ,
где  – амплитуда вынужденных колебаний, – амплитуда вынужденных колебаний,  – фаза колебаний, – фаза колебаний,  – отставание по фазе от частоты вынуждающей силы – отставание по фазе от частоты вынуждающей силы 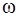
| ||
| Характеристики колебаний | 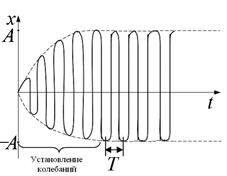
|  
| |
| Энергия колебаний | 
| ||

| при  
| ||
Примеры решения задач
Задача 1. Физический маятник представляет собой стержень длиной 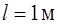 и массой
и массой  с прикрепленным к одному из его концов обручем диаметром
с прикрепленным к одному из его концов обручем диаметром  и массой
и массой  . Горизонтальная ось маятника проходит через середину стержня (точка
. Горизонтальная ось маятника проходит через середину стержня (точка 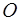 ) перпендикулярно ему (рис. 3.4). Определить период колебаний такого маятника.
) перпендикулярно ему (рис. 3.4). Определить период колебаний такого маятника.

Решение. Период колебаний физического маятника (3.14)
 ,
,
где 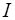 – момент инерции маятника относительно оси вращения,
– момент инерции маятника относительно оси вращения,  – масса маятника,
– масса маятника, 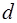 – расстояние от центра масс (точка
– расстояние от центра масс (точка  ) маятника до оси вращения.
) маятника до оси вращения.
Момент инерции маятника 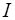 равен сумме моментов инерции стержня
равен сумме моментов инерции стержня  и кольца
и кольца  :
:
 , (1)
, (1)
где  ,
,  – в соответствии с теоремой Штейнера.
– в соответствии с теоремой Штейнера.  – момент инерции кольца относительно оси, проходящей через центр масс кольца,
– момент инерции кольца относительно оси, проходящей через центр масс кольца, 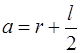 . Подставив выражения для
. Подставив выражения для  и
и  в (1), получим
в (1), получим 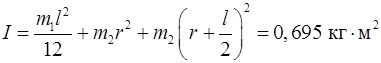 .
.
Расстояние от оси маятника до его центра масс равно
 .
.
Подставив полученные значения  ,
,  ,
,  ,
,  , получим период колебаний маятника
, получим период колебаний маятника
 .
.
Задача 2. Гиря массы 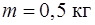 подвешена к пружине, жесткость которой
подвешена к пружине, жесткость которой  , и совершает затухающие колебания. Определить период этих колебаний, если за время двух колебаний амплитуда уменьшилась в 10 раз.
, и совершает затухающие колебания. Определить период этих колебаний, если за время двух колебаний амплитуда уменьшилась в 10 раз.
Решение. Период затухающих колебаний (см. таблицу 2.3)
|
|
|
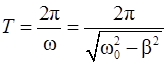 , (1)
, (1)
где 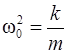 – собственная частота колебаний,
– собственная частота колебаний,  – коэффициент затухания, который связан с логарифмическим декрементом затухания соотношением
– коэффициент затухания, который связан с логарифмическим декрементом затухания соотношением
 , (2)
, (2)
 . (3)
. (3)
Здесь  по условию задачи, а
по условию задачи, а  , т.е.
, т.е.  , а
, а
 . (4)
. (4)
Подставим (4) в (1) и решим уравнение относительно периода 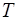 .
.
 ,
,
 ,
,
 .
.
Задачи к контрольной работе №1
| Вариант | Номера задач | |||||||
100. Тело вращается вокруг неподвижной оси. Изменение угла поворота со временем определяется формулой  , где
, где 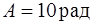 ,
,  ,
,  . Найти модуль полного ускорения точки, находящейся на расстоянии
. Найти модуль полного ускорения точки, находящейся на расстоянии  от оси вращения, для момента времени
от оси вращения, для момента времени  .
.
101. Колесо начало вращаться (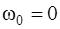 ) с постоянным угловым ускорением
) с постоянным угловым ускорением  . Через
. Через 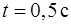 после начала движения полное ускорение колеса стало равно
после начала движения полное ускорение колеса стало равно  . Найти радиус колеса.
. Найти радиус колеса.
102. Две материальные точки движутся по прямой линии согласно уравнениям  и
и  , где
, где 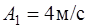 ,
,  ,
, 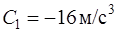 ,
,  ,
, 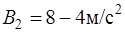 ,
,  . В какой момент времени ускорения этих точек будут одинаковыми? Найти скорость точек в этот момент.
. В какой момент времени ускорения этих точек будут одинаковыми? Найти скорость точек в этот момент.
103. Диск радиуса  вращается согласно уравнению
вращается согласно уравнению  , где
, где  ;
;  ;
;  . Определить тангенциальное
. Определить тангенциальное  , нормальное
, нормальное  и полное
и полное  ускорения точки на окружности диска для момента времени
ускорения точки на окружности диска для момента времени  .
.
104. Точка движется по дуге окружности радиуса 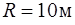 . В некоторый момент времени нормальное ускорение точки
. В некоторый момент времени нормальное ускорение точки  , вектор полного ускорения
, вектор полного ускорения 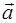 образует в этот момент с вектором нормального ускорения
образует в этот момент с вектором нормального ускорения  угол
угол  . Найти скорость и тангенциальное ускорение точки.
. Найти скорость и тангенциальное ускорение точки.
105. Две материальные точки в момент  начинают двигаться вдоль оси
начинают двигаться вдоль оси  согласно
согласно  ,
,  , где
, где 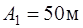 ,
,  ,
,  ,
,  ,
,  ,
,  . Найти скорости и ускорения этих точек в момент их встречи.
. Найти скорости и ускорения этих точек в момент их встречи.
106. Материальная точка движется вдоль прямой линии согласно уравнению  , где
, где 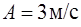 ,
,  . Найти путь, пройденный телом от момента времени
. Найти путь, пройденный телом от момента времени  до момента времени
до момента времени  .
.
|
|
|
107. Тело движется по окружности радиусом  . Зависимость пути от времени дается уравнением
. Зависимость пути от времени дается уравнением  , где
, где  . Найти нормальное
. Найти нормальное  и тангенциальное
и тангенциальное  ускорения точки в момент, когда линейная скорость точки
ускорения точки в момент, когда линейная скорость точки  .
.
108. Точка движется по окружности радиусом  . Закон ее движения выражается уравнением
. Закон ее движения выражается уравнением  , где
, где  ,
,  . Найти момент времени
. Найти момент времени  , в который нормальное ускорение точки
, в который нормальное ускорение точки  , Найти скорость
, Найти скорость 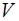 , тангенциальное
, тангенциальное  и полное
и полное  ускорения точки в этот момент времени.
ускорения точки в этот момент времени.  - координата, отсчитываемая вдоль окружность.
- координата, отсчитываемая вдоль окружность.
109. Материальная точка движется по окружности так, что зависимость пути от времени дается уравнением  , где
, где  ,
,  и
и  . Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорения через
. Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорения через  после начала движения, если известно, что нормальное ускорение точки при
после начала движения, если известно, что нормальное ускорение точки при  равно
равно  .
.
110. Частица начала движение из начала координат. Скорость ее зависит от времени по закону  . Найти координаты частицы через
. Найти координаты частицы через  после начала движения, если
после начала движения, если 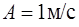 ,
,  ?
?
111. Частица начала движение из точки с координатами  ;
; 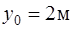 ;
; 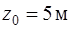 с нулевой начальной скоростью. Ее скорость зависит от времени по закону
с нулевой начальной скоростью. Ее скорость зависит от времени по закону  . Найти координаты частицы через
. Найти координаты частицы через 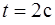 после начала движения.
после начала движения.  ,
,  ,
,  .
.
112. Частица начала движение (с нулевой начальной скоростью) из начала координат. Ее ускорение зависит от времени по закону  . Найти модуль скорости частицы в момент времени
. Найти модуль скорости частицы в момент времени  , если
, если  ;
;  ;
;  ;
;  ;
;  .
.
113. Частица начала свое движение из начала координат с начальной скоростью  и с ускорением, которое зависит от времени по закону
и с ускорением, которое зависит от времени по закону 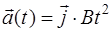 . Каков модуль скорости частицы в момент времени
. Каков модуль скорости частицы в момент времени 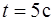 , если
, если 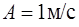 ;
;  ?
?
114. Нормальное ускорение точки, движущейся по окружности радиусом  , задается уравнением
, задается уравнением 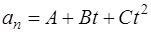 . Определите: а) тангенциальное ускорение точки; б) полное ускорение точки в момент времени
. Определите: а) тангенциальное ускорение точки; б) полное ускорение точки в момент времени  .
. 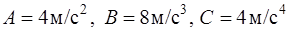 .
.
115. Материальная точка движется из начала координат вдоль оси  с нулевой начальной скоростью. Ее ускорение линейно растет и за первые
с нулевой начальной скоростью. Ее ускорение линейно растет и за первые  достигает значения
достигает значения  . Определите в конце десятой секунды: а) скорость точки; б) пройденный точкой путь.
. Определите в конце десятой секунды: а) скорость точки; б) пройденный точкой путь.
116. Частица начала двигаться из начала координат с начальной скоростью  и с ускорением, которое зависит от времени по закону
и с ускорением, которое зависит от времени по закону  . Каков модуль скорости частицы в момент времени
. Каков модуль скорости частицы в момент времени 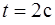 , если
, если  ;
;  ;
;  .
.
|
|
|
117. Частица начала двигаться из точки с радиус-вектором  со скоростью, которая зависит от времени по закону
со скоростью, которая зависит от времени по закону  . На каком расстоянии от начала координат будет находится частица в момент времени
. На каком расстоянии от начала координат будет находится частица в момент времени  , если
, если 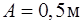 ;
; 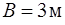 ;
;  ?
?
118. Частица начала двигаться из точки с радиус-вектором  со скоростью, которая зависит от времени по закону
со скоростью, которая зависит от времени по закону  . На какое расстояние от начала координат удалится частица в момент времени
. На какое расстояние от начала координат удалится частица в момент времени 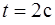 , если
, если 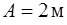 ;
;  ;
;  ;
;  ?
?
119. Частица начала двигаться из начала координат с нулевой начальной скоростью. Ее ускорение зависит от времени по закону 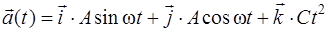 . Каков модуль скорости частицы в момент времени
. Каков модуль скорости частицы в момент времени 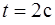 , если
, если 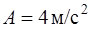 ;
; 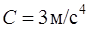 ;
;  ?
?
120. Тело массой  движется прямолинейно по закону
движется прямолинейно по закону  .
.  ;
;  ;
;  ;
; 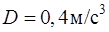 . Определите силу, действующую на тело через две секунды после начала движения.
. Определите силу, действующую на тело через две секунды после начала движения.
121. Тело массой  движется так, что зависимость пройденного пути от времени описывается уравнением
движется так, что зависимость пройденного пути от времени описывается уравнением  , где
, где 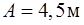 ,
, 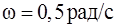 . Запишите закон изменения силы как функцию времени. Определите модуль силы, действующей на тело, через
. Запишите закон изменения силы как функцию времени. Определите модуль силы, действующей на тело, через  после начала движения.
после начала движения.
122. Груз массой 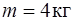 вращается на канате длиной
вращается на канате длиной  в горизонтальной плоскости, совершая
в горизонтальной плоскости, совершая 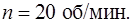 Какой угол с вертикалью образует канат и какова сила его натяжения?
Какой угол с вертикалью образует канат и какова сила его натяжения?
123. Через блок, укрепленный на потолке комнаты, перекинута нить, на концах которой подвешены тела с массами  и
и  . Массы блока и нити пренебрежимо малы, трение можно не учитывать. Найти ускорение центра масс этой системы.
. Массы блока и нити пренебрежимо малы, трение можно не учитывать. Найти ускорение центра масс этой системы.
124. Наклонная плоскость, образующая угол  с плоскостью горизонта, имеет длину
с плоскостью горизонта, имеет длину 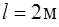 . Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время
. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время 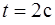 . Определить коэффициент трения
. Определить коэффициент трения 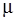 тела о плоскость.
тела о плоскость.
125. В вагоне укреплен отвес (шарик массой  на нити). Вагон скатывается без трения с наклонной плоскости, образующей угол
на нити). Вагон скатывается без трения с наклонной плоскости, образующей угол  с горизонтом. Считая отвес неподвижным относительно вагона, определите на какой угол
с горизонтом. Считая отвес неподвижным относительно вагона, определите на какой угол  отклонится отвес от нормали к наклонной плоскости.
отклонится отвес от нормали к наклонной плоскости.
126. Цилиндр массы  и радиуса
и радиуса  может вращаться вокруг своей закрепленной горизонтальной оси симметрии О, причем на него действует при этом постоянный момент сил трения
может вращаться вокруг своей закрепленной горизонтальной оси симметрии О, причем на него действует при этом постоянный момент сил трения  (см. рис.1). С какой силой
(см. рис.1). С какой силой  надо тянуть намотанную на цилиндр нить, чтобы за время
надо тянуть намотанную на цилиндр нить, чтобы за время  угловая скорость цилиндра увеличилась на
угловая скорость цилиндра увеличилась на  ?
?
|
|
|
127. На однородный диск, способный вращаться без трения вокруг горизонтальной оси О, намотана нить, к концу которой прикреплена гиря, опускающаяся с ускорением  , где
, где 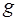 - ускорение свободного падения (рис.2). Во сколько раз масса диска
- ускорение свободного падения (рис.2). Во сколько раз масса диска  больше массы гири
больше массы гири  ?
?

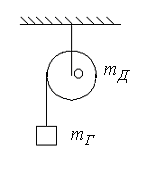
Рис.1 Рис.2
128. Тонкий стержень массой  и длиной
и длиной  начинает вращаться с угловой скоростью
начинает вращаться с угловой скоростью  вокруг оси перпендикулярной оси стержня и проходящей через центр масс. Чему равен постоянный момент сил трения, действующий на стержень при вращении, если он останавливается, повернувшись на угол
вокруг оси перпендикулярной оси стержня и проходящей через центр масс. Чему равен постоянный момент сил трения, действующий на стержень при вращении, если он останавливается, повернувшись на угол  ?
?
129. Небольшой брусок начинает под действием силы тяжести скользить без начальной скорости и без трения с ледяной горки высотой  , поверхность которой составляет
, поверхность которой составляет  к горизонту (рис.3). За какое время предмет соскользнет с горки?
к горизонту (рис.3). За какое время предмет соскользнет с горки?
130. Однородный цилиндр начинает скатываться с начальной скоростью  по наклонной плоскости с углом
по наклонной плоскости с углом  без проскальзывания (рис.4). Какой путь должен проделать цилиндр, чтобы его скорость возросла в 5 раз?
без проскальзывания (рис.4). Какой путь должен проделать цилиндр, чтобы его скорость возросла в 5 раз?


Рис.3 Рис.4
131. Предмет массы  стоит на горизонтальном диске массы
стоит на горизонтальном диске массы  и радиуса
и радиуса  на расстоянии
на расстоянии  от центра диска. Диск вместе с предметом вращается без трения вокруг закрепленной оси, проходящей через центр диска (рис.5). В процессе вращения предмет соскальзывает к краю диска. Угловая скорость вращения диска с предметом, находящимся на краю диска вдвое меньше первоначальной. Чему равна масса
от центра диска. Диск вместе с предметом вращается без трения вокруг закрепленной оси, проходящей через центр диска (рис.5). В процессе вращения предмет соскальзывает к краю диска. Угловая скорость вращения диска с предметом, находящимся на краю диска вдвое меньше первоначальной. Чему равна масса  предмета?
предмета?
132. Два тонких горизонтальных диска вращались свободно без трения в разные стороны вокруг общей вертикальной закрепленной оси, проходящей через центры дисков. (рис.6). Масса нижнего диска в 4 раза больше, чем масса верхнего, а радиус нижнего в 2 раза больше радиуса верхнего диска. Верхний диск упал вниз и оба диска, слипшись, стали вращаться вместе в направлении, в котором вращался верхний диск, с угловой скоростью  . Нижний диск до падения вращался с угловой скоростью
. Нижний диск до падения вращался с угловой скоростью  . Чему была равна угловая скорость верхнего диска
. Чему была равна угловая скорость верхнего диска  до падения?
до падения?
|
|
|


