СКАЛЯРНОЕ ЧАСТОТНОЕ УПРАВЛЕНИЕ АД ПО ЗАКОНУ М.П. КОСТЕНКО: УРАВНЕНИЯ, ХАРАКТЕРИСТИКИ, СВОЙСТВА.

Скаляр переменного напряжения представляется только величиной , полученной с помощью непосредственного измерения , расчета или преобразования мгновенных значений . Следовательно , общей чертой всех скалярных систем управления является модуль регулируемой величины .Эта скалярная величина используется как в разомкнутых , так и в замкнутых системах частотного управления асинхронными двигателями .

Скалярное частотное управление берет свое начало с 1925 года , когда М.П.Костенко предложил свой закон частотного управления

для идеализированного АД, в котором:

1. активное сопротивление R₁ обмотки статора равно нулю ,

2. отсутствуют потери в стали ,

3. магнитная система ненасыщена ,

4. имеется независимое охлаждение .

Для идеализированного АД этот закон управления обеспечивает постоянство перегрузочной способности: (8.100)

и экономичное регулирование электрических машин,

где критический момент АД при текущей и номинальной частотах ,

статический момент при текущей угловой скорости двигателя и при номинальной скорости .

При этом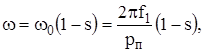

где s – скольжение , - число пар полюсов обмотки статора АД .

При использовании относительных безразмерных единиц :

(8.102)

закон М.П.Костенко записывается в виде :

Как показал А.А.Булгаков , закон частотного управления М.П.Костенко относится не только к частотному управлению , а вообще к любому управлению электродвигателем . В частности , при параметрическом управлении , когда

(8.104)

Если учесть , что в идеализированном двигателе = 0 , то

Следовательно , напряжение , подводимое к АД , надо изменять с изменением нагрузки. Этот принцип управления широко используется в современных асинхронных электроприводах для экономии электроэнергии , когда в цепь статора АД включаются полупроводниковые преобразователи напряжения , которые изменяют свое выходное напряжение (первую гармонику) пропорционально корню квадратному из относительного момента (тока) двигателя.

 

Представим статический момент в общем виде :

(8.106)

где n = -1, 0 ,1 ,2 .

Принимая

получим

(8.107)

Представляя пропорцию (8.100) в виде

(8.108)

находим

(8.109)

При R₁=0 формула Клосса имеет вид

(8.110)

где s и s_к – текущее и критическое скольжение АД при данной частоте f₁ .

Критическое скольжение при R₁ = 0 :

(8.111)

где (8.112)

X_к.ном – индуктивное сопротивление контура короткого замыкания АД при номинальной частоте ,

R^/₂ – активное сопротивление фазы ротора , приведенное к статору .

При подстановке (8.111) в (8.110) , получаем :

(8.113)

Поскольку

(8.114)

то

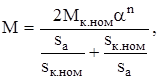(8.115)

(8.116)

где s_а- абсолютное скольжение .

Представив электромагнитный момент М и угловую скорость w ротора в относительных безразмерных единицах

(8.117)

получим из (8.115) и (8.116) параметрическое уравнение семейства механических характеристик идеализированного АД , управляемого по закону М.П.Костенко :

(8.118)

где в качестве параметров выступают :

1. абсолютное скольжение s_а ,

2. относительная частота a ,

3. характер статического момента , определяемый степенью n ( n = -1, 0, 1, 2 ).

Из (8.118) следует , что при постоянном статическом моменте (n=0) , частотное управление АД происходит при постоянном критическом моменте (m_к = l_m ) и механические характеристики представляют собой семейство конгруэнтных кривых ( Рис.8.11) .

Если частотное управление осуществляется при квадратичном статическом моменте (n=2) , то критический момент пропорционален квадрату частоты (m_к = l_ma² ) и механические характеристики имеют вид , показанный на Рис.8.12 . При управлении АД с поддержанием постоянства мощности ( n = -1 ) , критический момент изменяется обратно пропорционально частоте (m_к = l_ma^-1 ).Обычно такое регулирование скорости применяется при a>1 (Рис.8.13) .

Функциональная схема разомкнутой системы частотного управления АД показана на Рис.8.19. Обратная связь по напряжению служит здесь только для поддержания соотношения между управляющими величинами, заданными системой управления : g = F(a) . Она исключает влияние нелинейности регулятора напряжения РН и влияние потерь в силовом блоке ПЧ , но не затрагивает сущности регулирования , которое осуществляется независимо от нагрузки .

Недостатки разомкнутых систем частотного управления устраняются в замкнутых системах , когда напряжение на двигателе изменяется не только в функции частоты , но и тока (момента ) нагрузки . При этом магнитный поток и перегрузочная способность двигателя поддерживаются на заданном уровне.

34 СКАЛЯРНОЕ ЧАСТОТНОЕ УПРАВЛЕНИЕ АД ПО ЗАКОНУ Y₁= const.

На основании и можно записать пропорцию :

(8.144)

из которой определяется действующее значение ЭДС статора : (8.145)

при частотном управлении по закону Y₁= const.

(8.146)

где (8.147)

K_s – коэффициент магнитной связи статора .Из Рис.8.21 и принятых обозначений (8.146) следует , что приведенный ток ротора :

(8.148) (8.149)

где действующее значение номинальной ЭДС статора E_s.ном : (8.150)

Электромагнитный момент трехфазного АД можно записать в виде (8.151)

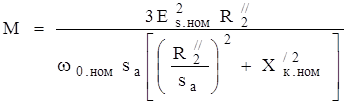(8.152)

абсолютное критическое скольжение (8.154)

Определим ток , соответствующий абсолютному критическому скольжению: и электромагнитную мощность :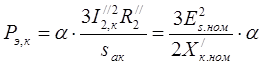

Критический (максимальный ) электромагнитный момент :

Механические характеристики асинхронного двигателя при частотном управлении по закону Y₁= const выражаются параметрическим уравнением

Критические моменты АД при Y₁= const и на естественной характеристике для двигательного режима относятся как : (8.162)

Для токов , соответствующих критическим скольжениям , имеем отношение

Отношение (8.162) показывает , что критический момент АД при частотном управлении по закону Y₁= const близок к критическому моменту двигателя на естественной характеристике .

где

При реализации этого закона частотного управления необходимо обеспечивать на обмотках статора АД напряжение

(8.166)где и ,

При этом , по обмоткам фаз статора будет протекать ток

---

Рекомендуемые страницы:

Воспользуйтесь поиском по сайту: