КПД и коэффициент мощности нерегулируемого электропривода

Сначала рассмотрим к.п.д. и коэффициент мощности нерегулируемого электропривода. К.п.д. нерегулируемого электропривода представляет собой отношение мощности Р_р.0 на рабочем органе машины к мощности Р₁, потребляемой из сети:

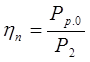где (6.54)

h_n, h_д – соответственно к.п.д. механической передачи и к.п.д. электродвигателя,

Р₂ – мощность на валу электродвигателя.

Если принять для рабочего участка естественной механической характеристики, где скорость незначительно изменяется, коэффициент загрузки

то, используя (6.17), к.п.д. электродвигателя можно записать таким образом:

, (6.57) где ,

Подставив выражение коэффициента А через номинальный к.п.д. h_ном и коэффициент потерь а в (6.57), получим окончательное выражение для к.п.д. нерегулируемого электродвигателя (6.59)

Из (6.59) видно, что к.п.д. нерегулируемого электродвигателя является сложной функцией коэффициента загрузки К_з. Значение оптимального коэффициента загрузки, при котором к.п.д. достигает максимальной величины, определяем из решения уравнения

, (6.60) т.е. (6.61) Подставив (6.61) в (6.59), найдем максимум к.п.д. Определим переменные потери мощности при оптимальном коэффициенте загрузки:

,

следовательно, максимум к.п.д. достигается, когда постоянные потери становятся равными переменным.

При а<1 максимум к.п.д. имеет место при нагрузке, меньше номинальной, а при а>1 – больше номинальной. Если а=1 то максимум к.п.д. соответствует номинальному к.п.д. (рис.6.5).

Обычно электродвигатели длительного режима (s1) проектируют таким образом, чтобы максимум к.п.д. был при коэффициенте загрузки К_з=0,75. этим самым учитывается возможность и наибольшая вероятность работы электродвигателя в режиме s1 с небольшой недогрузкой. С ростом мощности к.п.д. электродвигателя возрастает.

Для электрических двигателей переменного тока важным энергетическим показателем является коэффициент мощности, который при синусоидальных токах и напряжения cosj: ,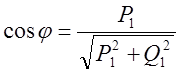

где Р₁ – потребляемая электродвигателем активная мощность.

Q₁ – “потребляемая” реактивная мощность из сети.

Для трехфазного асинхронного двигателя 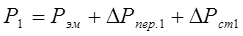,(6.65) , (6.66)

где – намагничивающий ток, ток статора и приведенный ток ротора,

– индуктивные сопротивления намагничивающего контура, рассеяния статора и ротора (приведенное).

Реактивную мощность Q₁ можно выразить через активную Р1, используя треугольник мощностей: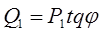

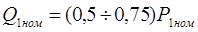
Для большинства асинхронных двигателей cosj_ном»0,8¸0,9, что дает

Характер зависимости cosj от коэффициента загрузки показан на рис.6.6.

 

Поскольку потери мощности в активных сопротивлениях R источника, линии и приемника определяются полным током I, то при заданной активной мощности Р=Р_ср эти потери будут равны

,

где I_а – активная составляющая полного тока I,

DР_n.т – потери при передачи мощности Р постоянным током (I_а=I_n.т).

выражение (6.69) показывает, что cosj является энергетической характеристикой, определяющей экономичность потребления активной энергии на переменном токе, с увеличением cosj уменьшаются потери при передаче заданной активной мощности от источника приемнику электроэнергии.

В синхронном двигателе cosj зависит от нагрузки так же, как и в асинхронном.

15. К.П.Д. И КОЭФФИЦИЕНТ МОЩНОСТИ РЕГУЛИРУЕМОГО ЭЛЕКТРОПРИВОДА.

Все способы регулирования скорости электроприводов можно разделить на две группы. 1ая- при которых скорость идеального холостого хода w₀ электродвигателя остается постоянной. 2ая - скорость идеального холостого хода w₀ электродвигателя изменяется с помощью управляющего воздействия. Для выявления особенностей к.п.д. регулируемого электропривода при w₀=const рассмотрим реостатное регулирование скорости ДПТ НВ. Запишем к.п.д ДПТ НВ в виде ,(6.70)

Для двигательного режима момент на валу М₂ можно выразить через электромагнитный момент М и потерю момента:

Для двигателей постоянного тока при регулировании скорости принимают

,

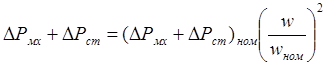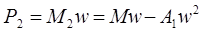, (6.73) где

При номинальном магнитном потоке .Разделим числитель и знаменатель (6.70) при всех подстановках выше на величину Р_НОМ=М_НОМω_НОМ, в результате получим (6.77)

где (6.78)

Если определить диапазон регулирования скорости: 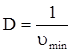(6.79)

Для электродвигателей нормального исполнения при μ=1 (6.81)

А теперь посмотрим, как будет изменятся к.п.д. асинхронного двигателя при ω₀=const и изменении угловой скорости ротора ω за счет скольжения s. K.п.д. асинхронного двигателя: (6.82)

При понижении скорости ротора с увеличением скольжения механические потери уменьшаются, а потери в стали ротора возрастают. Их сумму примерно можно считать постоянной, тогда (6.83)

Получаем к.п.д.

Для линейной части ест механической характеристики АД справедливо соотношение ,

Разделив числитель и знаменатель (6.84) на Р_НОМ=ω_НОММ_НОМ и принимая во внимание (6.85), найдем (6.86)

где 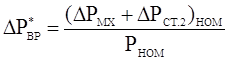(6.87) (6.88)

Рассмотрим к.п.д. и коэффициент мощности регулируемого электропривода при ω₀=var.

Если регулирование скорости ДПТ НВ осуществляется изменением подводимого напряжения при постоянном токе возбуждения, равном номинальному, то постоянные потери мощности в регулируемом ДПТ НВ

Для частотного регулирования АД по закону Ф=const имеем (6.90) где m=1,3÷1,5; .

Если не учитывать постоянные величины потерь на создание магнитного поля ( и ), то постоянные потери ДПТ НВ и АД будут примерно пропорциональны квадрату относительной скорости

примем, что

Введем коэффициент загрузки двигателя моментом (6.93)

С учетом этих обозначений определяем мощность на валу электродвигателя

и суммарные потери мощности

где К.п.д. регулируемого электродвигателя определяется отношением мощности на валу к потребляемой мощности:

 

к.п.д. 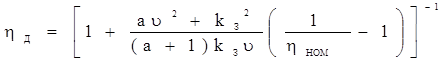является функцией двух независимых переменных (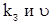), где в качестве парам выступают ном к.п.д. и коэффициент потерь а.

Решив уравнение найдем оптимальный коэф загрузки регулируемого эд

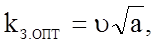(6.100) который соответствует равенству постоянных и переменных потерь.

Коэффициент полезного действия регулируемого электропривода включает произведение трех к.п.д.: управляемого преобразователя, электродвигателя и передаточного механизма, т.е.

Коэффициент мощности k_M определяется выражением

где Р – активная

,

 

16. ПОТЕРИ ЭНЕРГИИ В ПЕРЕХОДНЫХ ПРОЦЕССАХ ЭЛЕКТРОПРИВОДА(ω₀=CONST) .

Потери энергии в переходных процессах электропривода зависят от системы электропривода и способа формирования переходного процесса и в общем случае определяются выражением

где ΔP(t) – суммарные потери мощности в данный момент времени переходного процесса, t_П.П. – время переходного процесса.

Главнейшим фактором, определяющим потери энергии в переходном процессе, является характер изменения скорости ω₀ идеального холостого хода.

В электроприводах с ω₀=const управляющее воздействие изменяется скачком. Потери мощности в якорной цепи ДПТ НВ и в роторной цепи АД: ΔР= Р_ЭМ – Р_МХ=М(ω₀–ω)

Соответственно потери энергии будут равны разности электромагнитной А₁ и полной механической А₂ энергий электропривода: ΔА= А₁ – А₂

где 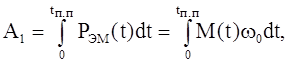(6.123)

Pассмотрим частный случай при М_С=0: М=М_ДИН=J ,

что при подстановке в (6.123) и (6.124) приводим к результату (6.126)

(6.127)

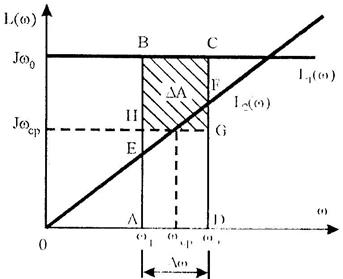где ω₁ и ω₂ – угловые скорости электродвигателя в начале и в конце переходного процесса, J – суммарный момент электропривода.Произведение Jω есть момент количества движения и имеет размерность H·м·с·рад.

Потери энергии в электроприводе можно записать в виде

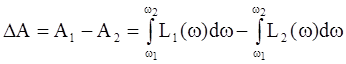
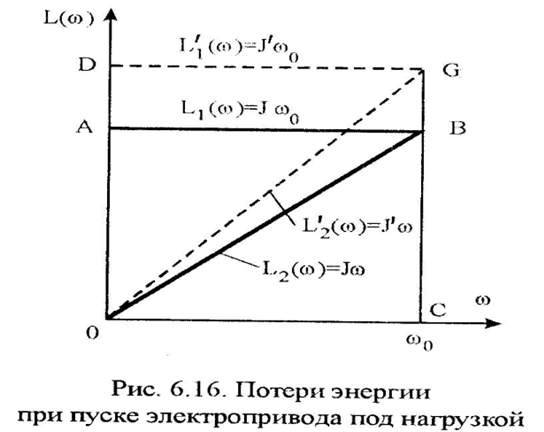
Где L₁(ω)=Jω₀, (6.132) L₂(ω)=Jω,

Соотношение (6.131) можно представить графически

Возьмем интегралы:

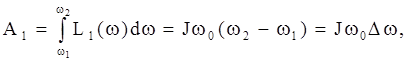(6.134) (6.135) где Δω = ω₂ – ω₁ ω_сρ= ½(ω₂ + ω₁) В результате можем записать общую формулу для определения потерь энергии в якорной (роторной) цепи электропривода за время переходного процесса при ω₀=const и М_С=0: ΔА₀ = JΔω(ω₀ – ω_сρ) при ω₀=const и М_С=0.

Пуск вхолостую: ω₁=0; ω₂=ω₀; ω_сρ= ½(ω₂ + ω₁)= ½ ω₀; Δω = ω₂ – ω₁= ω₀. Находим А₁=Jω₀Δω=J ; А₂=Jω_сρΔω= ½ J ; ΔА_по=А₁ – А₂=J – ½ J = .

 

Динамическое торможение вхолостую:

ω₁=ω₀; ω₂=0; ω_сρ= 0,5(ω₂ + ω₁)= 0,5ω₀; Δω = ω₂ – ω₁= –ω₀.

Так как при динамическом торможении якорь электродвигателя отключен от силовой цепи, то L₁(ω)=0; А₁=0.

Полная механическая мощность: А₂=Jω_сρΔω= –½ J

и потери энергии ΔА_дто=А₁ – А₂=0–(-½ J )= .

Следовательно, при динамическом торможении вхолостую потери энергии равны запасу кинетической энергии электропривода, так как при динамическом торможении теряется вся накопленная механическая энергия (рис.6.13). поэтому при динамическом торможении вхолостую потери энергии равны потерям энергии при пуске вхолостую.

Торможение противовключением в холостую:

ω₁=ω₀; ω₂=0; ω₀<0; ω_сρ= 0,5(ω₂ + ω₁)= 0,5ω₀; Δω = ω₂ – ω₁=0–ω₀= –ω₀.

Вычисляем: А₁=Jω₀Δω=J(-ω₀)(-ω₀)=J ; А₂=Jω_сρΔω= ½ J (-ω₀)= –½J ; ΔА_пр.о=А₁ – А₂=J –(–½ J )=

Реверс вхолостую:

ω₁=ω₀; ω₂= –ω₀; ω₀<0; ω_сρ= 0,5(ω₂ + ω₁)= 0; Δω = ω₂ – ω₁= –2ω₀.

Определяем: А₁=Jω₀Δω=J(-ω₀)(-2ω₀)=2J ;

А₂=Jω_сρΔω= J·0·(-2ω₀)=0;

ΔА_рев.о=А₁–А₂=2J =

Полученные соотношения соответствуют потерям энергии в якоре ДПТ НВ и в роторе АД. Потери энергии ΔА₁ в статоре АД определяются через потери ΔА₂ в роторе таким образом

Теперь можно записать суммарные потери энергии в асинхронном двигателе в переходном процессе электропривода вхолостую:

Где (6.141)

(6.142)

 

16 ПОТЕРИ ЭНЕРГИИ В ПЕРЕХОДНЫХ ПРОЦЕССАХ ЭЛЕКТРОПРИВОДА(ω₀=const) .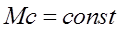

Потери энергии в переходных процессах электропривода зависят от системы электропривода и способа формирования переходного процесса:

Главнейшим фактором, определяющим потери энергии в переходном процессе, является характер изменения скорости ω₀ идеального холостого хода.

Потери мощности в якорной цепи ДПТ НВ и в роторной цепи АД:

ΔР= Р_ЭМ – Р_МХ=М(ω₀–ω)

Соответственно потери энергии будут равны разности электромагнитной А₁ и полной механической А₂ энергий электропривода:

ΔА= А₁ – А₂

Примем допущение, что в переходном процессе электромагнитный момент эд равен его среднему значению М_СР.

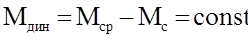
М(t)=М_ср= М_с+ М_дин

Пусть тогда , ,

Потери энергии в переходном процессе при допущении будут равны:

,

17 ПОТЕРИ ЭНЕРГИИ В ПЕРЕХОДНЫХ ПРОЦЕССАХ ЭЛЕКТРОПРИВОДА ПРИ ω₀=var

В общем случае потери энергии в переходном процессе электропривода при плавном управляющем воздействии можно записать так:

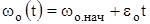, , (2)где

Для получения наглядного представления о потерях энергии в переходном процессе примем допущения: , , соотношения между величинами сохраняются на всем интервале переходного процесса,статическая скорость равна конечному значению.

что позволяет электромагнитную энергию А₁ записать в виде

, (6) где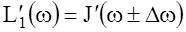

Полная механическая энергия А₂ за время переходного процесса электропривода

Потери энергии за время переходного процесса ,

г , (10) ,

При торможении электропривода возможны случаи:

а) Когда тогда

б) Когда тогда

в) и 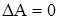, что соответствует свободному выбегу.

При М_с=0: , ,

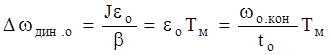
Обычно , значит, использование линейного задания скорости идеального холостого хода позволяет уменьшить потери энергии по сравнению с прямым пуском в 5 и более раз

18 Выбор электродвигателей: общие сведения.

Электропривод должен в наибольшей степени соответствовать условиям работы механизма, приводимого им в движение. Только в этом случае можно обеспечить высокопроизводительную, надежную и экономичную работу технологической установки. Поэтому электропривод проектируется совместно с проектированием рабочей машины и технологического процесса.

По технико-экономическим соображениям в общем случае электропривод должен удовлетворять ряду требований, иногда противоречивых:

1) иметь минимально возможные габариты и массу,

2) иметь низкую стоимость,

3) обеспечивать высокую надежность работы,

4) быть простым в управлении,

5) не оказывать вредного влияния на питающую сеть,

6) не создавать помех для работы других электропотребителей

Чтобы выполнить эти требования, необходимо последовательно решить следующие вопросы:

1) изучить особенности работы исполнительного механизма и выполнения технологического процесса,

2) выбрать тип электропривода (регулируемый или нерегулируемый),

3) выбрать род тока и тип электродвигателя,

4) выбрать напряжение и частоту питающей сети,

5) произвести расчет мощности и выбрать электродвигатель и передаточный механизм (если он предварительно не задан),

6) разработать систему управления и выбрать ее элементы,

7) сделать технико-экономическое обоснование выбранного варианта,

8) выполнить конструктивную разработку узлов и размещение электрооборудования на промышленной установке.

В установках, где не требуется регулирования скорости по технологическим условиям, обычно применяют асинхронные двигатели с короткозамкнутым ротором как наиболее дешевые, надежные в работе и имеющие высокие коэффициенты полезного действия и коэффициент мощности. Но недостатком являются большие пусковы и тормозные токи, а также удары в механической передаче, следует рассмотреть вопрос возможности и целесообразности использования устройств мягкого пуска и торможения. Если по технологическим условиям возможна достаточно длительная работа асинхронного двигателя с небольшими нагрузками, то следует оценить целесообразность применения полупроводникового регулятора напряжения, работающего автоматически в функции загрузки электродвигателя.

Регулирование ЭП об ычно рассматривается от простейший до более сложных:

1)многоскоростные АД (полюсно-переключаемые).

2) асинхронные двигатели с фазным ротором и реостатным (дискретным или импульсным) регулированием скорости,

3)частотное регулирование

4)Регулирование ЭП постоянного тока

5)каскадные схемы

Определение мощности и выбор электродвигателя является наиболее трудоемким и ответственным этапом проектирования электропривода. Применение двигателей завышенной мощности приводит к увеличению капитальных затрат и эксплуатационных расходов, связанных со снижением КПД и коэффициента мощности (для АД). Если выбран двигатель недостаточной мощности, то при этом возникают тепловые перегрузки, ускоренное старение изоляции, понижение надежности работы и возможность аварии.

Длительное воздействие нагрузки на двигатель ограничивается допустимым нагревом, а кратковременное – перегрузочной способностью: , (7.1)

В асинхронном двигателе максимальный (критический) момент М_к зависит от квадрата напряжения. Поэтому допустимый критический момент М_к.доп определяют с учетом возможного снижения напряжения на 10%: , (7.2)

Перегрузочная способность асинхронных двигателей на естественной механической характеристике составляет .

Для синхронных двигателей максимальный момент определяется возможностью устойчивой работы в синхронном режиме. Для синхронных двигателей . Ограничение по нагреву электродвигателей определяется теплостойкостью их изоляции.

Режимы работы ЭД: 1) длительная работа с мало меняющейся нагрузкой 2) динамические,с меняющейся нагрузкой.

Вторая группа электродвигателей предназначена для механизмов с частыми пусками, торможениями, реверсами и большой частотой включений. В своем большинстве это механизмы кратковременного и повторно-кратковременного режимов работы. Характерной особенностью электродвигателей второй группы является повышенная перегрузочная способность (электрическая и механическая), уменьшенные потери энергии на разгон (меньший диаметр и большая длина ротора), обеспечение большой частоты включений.

Электродвигатели выбирают:по мощности, скорости, напряжению, току, условиям эксплуатации и монтажа. Выбор двигателей по мощности выполняют в соответствии с нагрузочными диаграммами механизмов и режимами работы.

Скорость электродвигателя выбирается такой, чтобы обеспечить необходимый технологический процесс производственного механизма. При заданном передаточном числе редуктора или другой передачи этот вопрос решается однозначно. Если передаточное число не задано, то его выбирают оптимальным, исходя из определенного критерия: быстродействия, минимуму потерь, минимума массы редуктор-двигатель и т.д.

Напряжение электродвигателя выбирается, исходя из номинального напряжения источника питания. При известной мощности и напряжении однозначно определяется ток электродвигателя.

При выборе электродвигателя необходимо учитывать условия эксплуатации, под которыми понимают воздействие климатических факторов, а также состояние окружающей среды.
19 НАГРЕВ И ОХЛАЖДЕНИЕ ЭЛЕКТРОДВИГАТЕЛЕЙ.

Потери электроэнергии в двигателе превращаются в теплоту, вследствие чего двигатель нагревается. Отдельные части двигателя при работе нагреваются неодинаково. Выделение тепла в различных режимах также неодинаково.

Для упрощения анализа тепловых процессов, происходящих в электродвигателе, на основе ряда допущений составляют тепловые модели. Наиболее простая тепловая модель основана на следующих допущениях:

1) двигатель представляет собой однородное в тепловом отношении тело, равномерно нагревающееся по всему объему (бесконечно большая теплопроводность) за счет источника мощности ,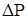

2) теплоотдача во внешнюю среду пропорциональна первой степени разности температур тела и охлаждающей среды,

3) температура охлаждающей среды постоянная.

Для такой модели (Рис.7.1) мощность теплового потока, передаваемая в окружающую среду, равна , где , , - температура перегрева, ^оС; А – теплоотдача в окружающую среду, Вт/^оС; S – площадь поверхности охлаждения, м²; - удельная теплоотдача при скорости охлаждающего воздуха , Вт/^оС м²; 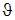- скорость охлаждающего воздуха, м/с; К – эмпирический коэффициент, принимаемый для электрических машин, равным примерно 0,8.

Величина, обратная теплоотдаче, называется тепловым сопротивлением Поэтому мощность теплового потока , -то,что подаётся в окружающую среду. Мощность теплового потока, идущего на нагрев тела, определяется выражением , ,

С_уд – удельная теплоемкость, Дж/^оС кг; m – масса тела, кг.

По закону сохранения энергии , Или , Полученное дифференциальное уравнение теплового баланса в одномассовой модели аналогично уравнению , (7.12)

электрической цепи, показанной на Рис.7.2, где имеем аналогии: ток ~ тепловой поток 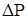, электрическое сопротивление R ~ тепловое сопротивление R_T, электрическая емкость С ~ теплоемкость с, электрический потенциал ~ температура тела , электрическое напряжение u ~ температура перегрева .

Поскольку для электрической цепи Рис.7.2 постоянная времени ,

и установившееся значение напряжения ,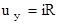

то (7.12) можно представить в виде ,

Аналогично имеем для уравнения тепловой модели , , где Т_Н – постоянная времени нагрева, - установившееся значение перегрева. , где 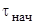- начальное значение температуры перегрева.

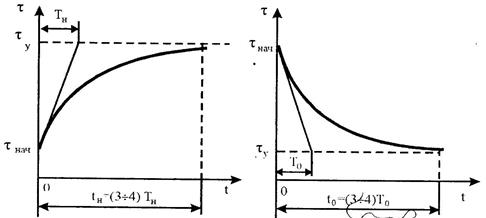Нагрев или охлаждение тела определяется начальным значением температуры: если , будет нагрев, если - охлаждение

Если скорость равна 0(двигатель отключён),то

если скорость равна номинальной –то постоянной нагрева T0>Tн (вентилятор отключён,нет охл)

Если скорость постоянна,то T0=Tн при независимой вентиляции

Одномассовая тепловая модель электродвигателя простая и удобная для анализа, но она лишь приближенно отражает нагрев обмоток. С целью повышения точности тепловых расчетов применяют двухмассовую модель, разделяя нагрев статора и ротора электродвигателя. В этом случае, принимая потери мощности в роторе и температуру внутренней поверхности статора постоянными, можем записать дифференциальное уравнение теплового равновесия ротора. -потери мощности ротора.С0-теплоёмкость среды.С1,С2-теплоёмкости статора,ротора..

Для установившегося состояния уравнение эквивалентной тепловой схемы имеет вид , где - средние температуры в точках Х и Y, - тепловой поток между точками Х и Y, R_xy – тепловое сопротивление между точками X и Y схемы.

Уравнения составляют для всех частей электродвигателя. Решение полученной системы уравнений, т.е. определение установившихся температур в разных точках эквивалентной схемы, возможно, если заранее определены тепловые сопротивления.

Уравнение Пуассона:

, , -удельные теплопроводности по осям х,у,z =ΔPэл/Vэл Ухудшение условий охлаждения для самовентилируемого двигателя:

Для самовентилируемого

β0=1-независимое охлаждение

β0=0,95-0,98-естественное охлаждение β0=0,45-0,55-закрытое исполнение

β0=0,25-0,35-защищённое исполнение

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: