 |
Тема 5. Линейные операторы. Тема 6. Квадратичные формы. Раздел II. Векторная алгебра. Тема 7. Векторная алгебра. Раздел III. Аналитическая геометрия
|
|
|
|
Тема 5. Линейные операторы.
Линейный оператор, действия над ними. Собственные векторы и собственные значения линейных операторов, их свойства и нахождение.
Литература: [1] –C. 202-221; [2] – C. 78-86.
Тема 6. Квадратичные формы.
Квадратичные формы. Закон инерции квадратичных форм. Положительно и отрицательно определённые квадратичные формы. Критерии знакоопределённости квадратичных форм.
Литература: [1] –C. 251-261; [2] – C. 86-91.
Раздел II. ВЕКТОРНАЯ АЛГЕБРА
Тема 7. Векторная алгебра.
Геометрические векторы на прямой, плоскости и в пространстве, действия над ними. Проекция вектора. Прямоугольная декартова система координат. Радиус-вектор. Координаты вектора. Линейные операции над векторами в координатной форме. Длина и направляющие косинусы вектора. Расстояние между точками. Деление отрезка в данном отношении. Скалярное, векторное, смешанное произведения векторов, их свойства, выражение в координатной форме, приложения для решения геометрических задач. Условия перпендикулярности, параллельности и компланарности векторов.
Литература: [1] –C. 5-37; [2] – C. 63-68; [3] – C. 301-305; [4] – C. 222-241.
Раздел III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Тема 8. Прямые линии и плоскости.
Прямая на плоскости и в пространстве. Различные виды уравнений прямой на плоскости ив пространстве. Расстояние от точки до прямой на плоскости. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Плоскость. Различные виды уравнений плоскости. Расстояние от точки до плоскости. Взаимное расположение прямой и плоскости.
Литература: [1] –C. 45-71; [2] – C. 95-104; 119-121;
|
|
|
[3] – C. 91-94; 305-311; [4] – C. 34-52; 244-252.
Тема 9. Кривые и поверхности второго порядка.
Кривые 2-ого порядка на плоскости: окружность, эллипс, гипербола, парабола, их определения, канонические уравнения, форма. Приведение общего уравнения кривой 2-ого порядка к каноническому виду и построение. Поверхности 2-ого порядка, их канонические уравнения и форма.
Литература: [1] –C. 72-110; [2] – C. 104-115; [3] – C. 95-98; 311-318;
[4] – C. 52-69; 252-259.
Тема 10. Системы линейных неравенств. Линейные задачи оптимизации.
Системы линейных неравенств. Решение линейных неравенств в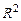 
. Постановка задачи линейного программирования, графический метод её решения.
Литература: [5] – C. 271-293.
3. Рекомендуемая литература.
Основная литература:
1. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М: Наука, 1998.
2. Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов. Учеб. пособие для вузов. -М.: ЮНИТИ-ДАНА, 1997.
3. Красс М. С. Математика для экономических специальностей. Учебник. –М.: ИНФРА-М, 1998.
4. Шипачев В. С. Высшая математика. Учебник для вузов. -М. Высшая школа, 2002.
5. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. В 2-х частях. Часть 1. Учеб. пособие для втузов. -М: Высшая школа, 1997.
6. Сборник задач по математике для втузов. Часть1. Линейная алгебра и основы математического анализа. Под ред. Ефимова А. В., Демидовича Б. П. -М: Наука, 1993.
Дополнительная литература:
7. Солодовников А. С., Бабайцев В. А., Браилов А. В. Математика в экономике: Учебник: В 2-х частях. Ч. 1. –М.: Финансы и статистика, 2000.
8. Общий курс высшей математики для экономистов. Учебник / Под ред. В. И. Ермакова. М: ИНФРА-М, 1999.
9. Зимина О. В., Кириллов А. И., Сальникова Т. А. Решебник. Высшая математика. М.: Физматлит, 2001.
|
|
|
10. Практикум по высшей математике для экономистов: Учеб. пособие для вузов/ Кремер Н. Ш., Тришин И. М., Путко Б. А. и др. Под ред. проф. Н. Ш. Кремера. –М.: ЮНИТИ-ДАНА, 2002.
11. Сборник задач по математике для вузов. Под ред. Котляра Л. М., Углова А. Н. -Наб. Челны: Изд-во КамПИ, 2004, 2006, 2007.
4. Методические указания по изучению дисциплины.
В процессе изучения данной дисциплины студенты должны сначала изучить теоретический материал и выработать навыки решения типовых задач, используя рекомендованную литературу, а затем выполнить одну контрольную работу (задания для контрольной работы приведены в разделе 5. 1 ).
При выполнении контрольной работы необходимо придерживаться указанных ниже правил:
1. Контрольная работа должна быть выполнена студентом в отдельной ученической тетради с полями не менее 3 см для замечаний преподавателя.
2. На обложке тетради указываются: название дисциплины; номер варианта и номера решаемых задач; Ф. И. О. студента, выполнившего работу, его номер группы и номер зачетной книжки; Ф. И. О. преподавателя, проверяющего работу (образец оформления обложки приведён в Приложении 3).
3. Номер варианта соответствует номеру студента в списке группы.
4. Номера решаемых задач выбираются из ТАБЛИЦЫ НОМЕРОВ ВЫПОЛНЯЕМЫХ ЗАДАНИЙ (Приложение 4).
5. Условия задач переписываются полностью, без сокращения слов, после чего приводится их подробное решение (чертежи можно выполнять аккуратно от руки). В конце решения приводится ответ.
6. В работу должны быть включены все задачи, указанные в задании, строго по порядку номеров. Контрольные работы, содержащие не все задания, а также задачи не своего варианта, не зачитываются.
7. Если в работе имеются ошибки, студент должен выполнить все требования преподавателя, изложенные в рецензии, и сдать работу с исправлениями на повторную проверку.
8. Никакие исправления в тексте уже проверенной работы не допускаются, все исправления записываются после рецензии преподавателя с указанием номера задачи, к которой относятся дополнения и исправления.
9. Работа может быть выполнена заново в случае выявления серьёзных замечаний и ошибок.
10. В конце тетради рекомендуется оставлять несколько чистых страниц для дополнений и исправлений.
|
|
|
После проверки контрольная работа предъявляется к защите. На защите студент должен показать свое умение решать задачи, подобные тем, что имеются в его контрольной работе.
Образец решения типового варианта контрольной работы приведён в Приложении 1.
|
|
|
