 |
1) ; 2) где - число;. Векторным произведением векторов и называется вектор , определяемый условиями: 1) ;
|
|
|
|
1); 2) где - число;
3)  ; 4)
; 4) 
5) 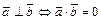 ; 6)
; 6) 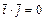 ,
,  ,
, 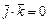 ,
,  ,
,  ,
, 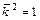 . Для векторов
. Для векторов  и
и  , заданных своими координатами
, заданных своими координатами  ,
, 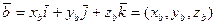 скалярное произведение вычисляется по формуле:
скалярное произведение вычисляется по формуле:  .
.
Скалярное произведение применяют: 1) для вычисления угла между векторами  и
и  по формуле:
по формуле: 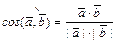 ; 2) для вычисления проекции вектора
; 2) для вычисления проекции вектора  на вектор
на вектор  по формуле:
по формуле:  ; 3) для вычисления длины вектора
; 3) для вычисления длины вектора 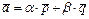 по формуле:
по формуле: 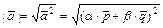 ; 4) в качестве условия перпендикулярности векторов
; 4) в качестве условия перпендикулярности векторов  и
и 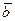 :
:  .
.
Векторным произведением векторов  и
и  называется вектор
называется вектор 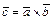 , определяемый условиями: 1)
, определяемый условиями: 1)  ;
;
2) 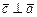 и
и  ; 3)
; 3) 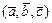 - правая тройка векторов.
- правая тройка векторов.
Упорядоченная тройка 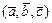 некомпланарных векторов называется правой тройкой, если из конца третьего вектора
некомпланарных векторов называется правой тройкой, если из конца третьего вектора  , кратчайший поворот от первого вектора
, кратчайший поворот от первого вектора  ко второму
ко второму  , виден совершающимся против хода часовой стрелки. В противном случае, тройка
, виден совершающимся против хода часовой стрелки. В противном случае, тройка 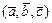 называется левой.
называется левой.
Векторное произведение обладает свойствами:
1); 2), где - число;
3); 4) 5);
6)  ,
, 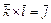 ,
,  ,
,  ,
, 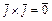 ,
, 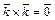 .
.
Для векторов  и
и  , заданных своими координатами
, заданных своими координатами  ,
, 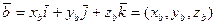 векторное произведение вычисляется по формуле:
векторное произведение вычисляется по формуле:  .
.
Векторное произведение 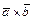 применяют: 1) для вычисления площадей треугольника и параллелограмма, построенных на векторах
применяют: 1) для вычисления площадей треугольника и параллелограмма, построенных на векторах  и
и  , как на сторонах, по формуле:
, как на сторонах, по формуле: 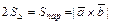 ; 2) в качестве условия параллельности векторов
; 2) в качестве условия параллельности векторов  и
и  :
:  .
.
Смешанным произведением упорядоченной тройки векторов  ,
,  и
и 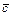 называется число
называется число 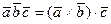 .
.
Смешанное произведение обладает свойствами:
1); 2);
3); 4) и -компланарны;
5) 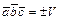 , где
, где  -объём параллелепипеда, построенного на векторах
-объём параллелепипеда, построенного на векторах  ,
,  и
и 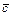 .
.
Для векторов  ,
,  и
и 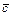 , заданных своими координатами
, заданных своими координатами  ,
, 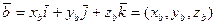 ,
,  смешанное произведение вычисляется по формуле:
смешанное произведение вычисляется по формуле: 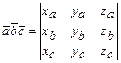 .
.
|
|
|
Смешанное произведение  применяют: 1) для вычисления объёмов тетраэдра и параллелепипеда, построенных на векторах
применяют: 1) для вычисления объёмов тетраэдра и параллелепипеда, построенных на векторах  ,
,  и
и  , как на рёбрах, по формуле:
, как на рёбрах, по формуле: 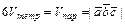 ; 2) в качестве условия компланарности векторов
; 2) в качестве условия компланарности векторов  ,
,  и
и 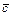 :
:  и
и  - компланарны.
- компланарны.
Тема 8. Прямые линии и плоскости.
Нормальным вектором прямой 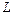 , называется всякий ненулевой вектор
, называется всякий ненулевой вектор  перпендикулярный данной прямой. Направляющим вектором прямой
перпендикулярный данной прямой. Направляющим вектором прямой 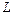 , называется всякий ненулевой вектор
, называется всякий ненулевой вектор  параллельный данной прямой.
параллельный данной прямой.
Прямая  на плоскости в системе координат
на плоскости в системе координат  может быть задана уравнением одного из следующих видов:
может быть задана уравнением одного из следующих видов:
1)  - общее уравнение прямой, где
- общее уравнение прямой, где 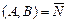 - нормальный вектор прямой;
- нормальный вектор прямой;
2)  - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку 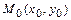 перпендикулярно данному вектору
перпендикулярно данному вектору  ;
;
3) 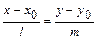 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку 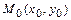 параллельно данному вектору
параллельно данному вектору  ( каноническое уравнение );
( каноническое уравнение );
4)  - уравнение прямой, проходящей через две данные точки
- уравнение прямой, проходящей через две данные точки  ,
, 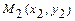 ;
;
5)  - уравнения прямой с угловым коэффициентом
- уравнения прямой с угловым коэффициентом  , где
, где 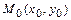 - точка через которую прямая проходит;
- точка через которую прямая проходит;  (
(  ) – угол, который прямая составляет с осью
) – угол, который прямая составляет с осью 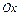 ;
; 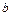 - длина отрезка (со знаком
- длина отрезка (со знаком 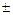 ), отсекаемого прямой на оси
), отсекаемого прямой на оси  (знак «
(знак «  », если отрезок отсекается на положительной части оси и «
», если отрезок отсекается на положительной части оси и « 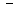 », если на отрицательной).
», если на отрицательной).
6)  - уравнение прямой в отрезках, где
- уравнение прямой в отрезках, где 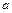 и
и 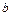 - длины отрезков (со знаком
- длины отрезков (со знаком 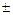 ), отсекаемых прямой на координатных осях
), отсекаемых прямой на координатных осях 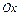 и
и  (знак «
(знак «  », если отрезок отсекается на положительной части оси и «
», если отрезок отсекается на положительной части оси и « 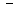 », если на отрицательной).
», если на отрицательной).
Расстояние от точки  до прямой
до прямой 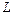 , заданной общим уравнением
, заданной общим уравнением  на плоскости, находится по формуле:
на плоскости, находится по формуле:
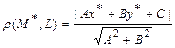 .
.
Угол 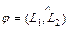 , (
, (  ) между прямыми
) между прямыми  и
и  , заданными общими уравнениями или уравнениями с угловым коэффициентом, находится по одной из следующих формул:
, заданными общими уравнениями или уравнениями с угловым коэффициентом, находится по одной из следующих формул:
 ;
;  .
.
 , если
, если 
 или
или  .
.
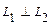 , если
, если  или
или 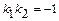
Координаты точки пересечения прямых  и
и  находятся как решение системы линейных уравнений:
находятся как решение системы линейных уравнений: 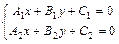 или
или 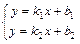 .
.
|
|
|
Нормальным вектором плоскости 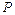 , называется всякий ненулевой вектор
, называется всякий ненулевой вектор  перпендикулярный данной плоскости.
перпендикулярный данной плоскости.
Плоскость 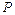 в системе координат
в системе координат  может быть задана уравнением одного из следующих видов:
может быть задана уравнением одного из следующих видов:
1)  - общее уравнение плоскости, где
- общее уравнение плоскости, где  - нормальный вектор плоскости;
- нормальный вектор плоскости;
2) 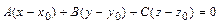 - уравнение плоскости, проходящей через точку
- уравнение плоскости, проходящей через точку 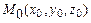 перпендикулярно данному вектору
перпендикулярно данному вектору  ;
;
3) 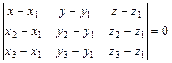 - уравнение плоскости, проходящей через три точки
- уравнение плоскости, проходящей через три точки  ,
, 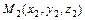 и
и  ;
;
4)  - уравнение плоскости в отрезках, где
- уравнение плоскости в отрезках, где 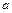 ,
, 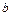 и
и 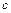 - дины отрезков (со знаком
- дины отрезков (со знаком 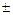 ), отсекаемых плоскостью на координатных осях
), отсекаемых плоскостью на координатных осях 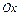 ,
,  и
и  (знак «
(знак «  », если отрезок отсекается на положительной части оси и «
», если отрезок отсекается на положительной части оси и « 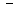 », если на отрицательной).
», если на отрицательной).
Расстояние от точки 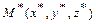 до плоскости
до плоскости 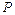 , заданной общим уравнением
, заданной общим уравнением 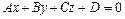 , находится по формуле:
, находится по формуле:
 .
.
Угол 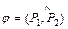 , (
, (  ) между плоскостями
) между плоскостями 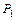 и
и 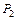 , заданными общими уравнениями, находится по формуле:
, заданными общими уравнениями, находится по формуле:
 .
.
 , если
, если 
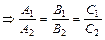
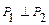 , если
, если  .
.
Тема 9. Кривые второго порядка.
Алгебраической кривой второго порядка в системе координат  называется кривая
называется кривая 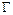 , общее уравнение которой имеет вид:
, общее уравнение которой имеет вид:
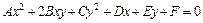 ,
,
где числа  - не равны нулю одновременно. Существует следующая классификация кривых второго порядка: 1) если
- не равны нулю одновременно. Существует следующая классификация кривых второго порядка: 1) если  , то общее уравнение определяет кривую эллиптического типа (окружность (при
, то общее уравнение определяет кривую эллиптического типа (окружность (при 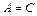 ), эллипс (при
), эллипс (при 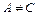 ), пустое множество, точку); 2) если
), пустое множество, точку); 2) если  , то - кривую гиперболического типа (гиперболу, пару пересекающихся прямых); 3) если
, то - кривую гиперболического типа (гиперболу, пару пересекающихся прямых); 3) если  , то - кривую параболического типа (параболу, пустое множество, прямую, пару параллельных прямых). Окружность, эллипс, гипербола и парабола называются невырожденными кривыми второго порядка.
, то - кривую параболического типа (параболу, пустое множество, прямую, пару параллельных прямых). Окружность, эллипс, гипербола и парабола называются невырожденными кривыми второго порядка.
Общее уравнение 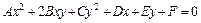 , где
, где  , определяющее невырожденную кривую (окружность, эллипс, гиперболу, параболу), всегда (методом выделения полных квадратов) можно привести к уравнению одного из следующих видов:
, определяющее невырожденную кривую (окружность, эллипс, гиперболу, параболу), всегда (методом выделения полных квадратов) можно привести к уравнению одного из следующих видов:
1а) 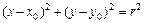 - уравнение окружности с центром в точке
- уравнение окружности с центром в точке  и радиусом
и радиусом 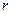 (рис. 5).
(рис. 5).
1б) 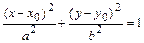 - уравнение эллипса с центром в точке
- уравнение эллипса с центром в точке 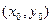 и осями симметрии, параллельными координатным осям. Числа
и осями симметрии, параллельными координатным осям. Числа 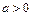 и
и 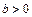 - называются полуосями эллипса; прямоугольник со сторонами
- называются полуосями эллипса; прямоугольник со сторонами  ,
,  параллельными осям симметрии и центром в точке
параллельными осям симметрии и центром в точке  - основным прямоугольником эллипса; точки пересечения основного прямоугольника с осями симметрии - вершинами эллипса.
- основным прямоугольником эллипса; точки пересечения основного прямоугольника с осями симметрии - вершинами эллипса.
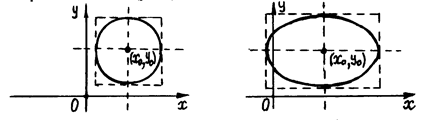
Для построения эллипса в системе координат  : 1) отмечаем центр
: 1) отмечаем центр 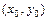 эллипса; 2) проводим через центр пунктирной линией оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром
эллипса; 2) проводим через центр пунктирной линией оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром 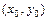 и сторонами
и сторонами  ,
,  параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон только в вершинах эллипса (рис. 6).
параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон только в вершинах эллипса (рис. 6).
|
|
|
Аналогично строится и окружность, основной прямоугольник которой имеет стороны  (рис. 5).
(рис. 5).
|
|
|


