5.2. Вопросы к экзамену.. Раздел I. Линейная алгебра.

116.

Отрасли производства	Отрасти потребления			Конечный продукт	Валовой продукт
	I	II	III
I
II
III
Чистый продукт
Валовой продукт

117.

Отрасли производства	Отрасти потребления			Конечный продукт	Валовой продукт
	I	II	III
I
II
III
Чистый продукт
Валовой продукт

118.

Отрасли производства	Отрасти потребления			Конечный продукт	Валовой продукт
	I	II	III
I
II
III
Чистый продукт
Валовой продукт

119.

Отрасли производства	Отрасти потребления			Конечный продукт	Валовой продукт
	I	II	III
I
II
III
Чистый продукт
Валовой продукт

120.

Отрасли производства	Отрасти потребления			Конечный продукт	Валовой продукт
	I	II	III
I
II
III
Чистый продукт
Валовой продукт

5. 2. Вопросы к экзамену.

Раздел I. Линейная алгебра.

1. Понятие матрицы. Частные виды матриц (квадратная, треугольная, диагональная, нулевая, единичная). Элементарные преобразования матриц. Понятие эквивалентности и равенства матриц.

2. Действия над матрицами (сложение, вычитание, умножение матрицы на число, умножение матрицы на матрицу) и их свойства. Линейная комбинация матриц.

3. Определители 2-ого и 3-егопорядка, их вычисление. Основные свойства определителей.

4. Понятие определителя n-ого порядка. Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя по элементам строки или столбца.

5. Понятие системы линейных уравнений (СЛУ). Частные виды СЛУ (квадратная, однородная, неоднородная). Матрица, расширенная матрица, определитель СЛУ.

6. Решение, множество решений, совместность, несовместность, определённость, неопределённость, эквивалентность СЛУ. Элементарные преобразования СЛУ, их основное свойство.

7. Теорема Крамера (о разрешимости СЛУ порядка ). Формулы Крамера для решения СЛУ, условия их применимости.

8. Метод Гаусса решения СЛУ, условия его применимости. Условия несовместности, определённости и неопределённости СЛУ по методу Гаусса.

9. Преобразования СЛУ, выполняемые при выполнении прямого и обратного ходов метода Гаусса. Базисные и свободные переменные. Нахождение общего решения СЛУ. Частные решения СЛУ.

10. Понятие обратной матрицы. Вырожденные и невырожденные матрицы. Теорема о существовании обратной матрицы. Основные способы нахождения обратной матрицы.

11. Матричные уравнения и их решение. Матричная форма записи СЛУ. Матричный способ (метод обратной матрицы) решения СЛУ и условия его применимости.

12. Однородные СЛУ, условия существования их ненулевых решений. Свойства частных решений однородных СЛУ.

13. Минор -ого порядка, базисный минор, ранг матрицы. Вычисление ранга матрицы. Критерий совместности СЛУ (теорема Кронеккера-Капелли).

14. Понятие -мерного арифметического вектора. Равенство векторов. Действия над векторами (сложение, вычитание, умножение на число). Линейная комбинация векторов.

15. Скалярное произведение арифметических векторов. Длина вектора и угол между векторами. Понятие ортогональности векторов.

16. Система векторов и её линейная комбинация. Понятие линейной зависимости и независимости системы векторов. Теорема о необходимом и достаточном условиях линейной зависимости системы векторов.

17. Понятие векторного пространства , евклидова пространства . Базис, канонический базис, ранг . Разложение вектора в  по векторам его базиса, координаты вектора. Теорема о единственности разложения вектора в данном базисе.

18. Понятие оператора, линейного оператора. Матрица линейного оператора. Сумма (разность) операторов, произведение оператора на число, произведение оператора на оператор, обратный оператор.

19. Понятие собственного числа и собственного вектора оператора. Характеристическое уравнение. Нахождение собственных чисел и векторов оператора.

20. Понятие квадратичной формы. Матрица квадратичной формы. Вырожденная, невырожденная, каноническая квадратичная форма. Закон инерции квадратичных форм.

21. Понятие знакоопределённости квадратичной формы. Главные миноры. Критерии знакоопределённости квадратичной формы.

 

Раздел II. Векторная алгебра.

22. Понятие геометрического вектора. Равенство векторов. Противоположный вектор. Орт вектора. Графические правила сложения, вычитания, умножения вектора на число. Проекция вектора на вектор.

23. Коллинеарность и компланарность векторов. Базис и канонический базис плоскости 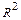; базис и канонический базис пространства . Координаты вектора.

24. Понятие декартовой системы координат в . Радиус-вектор, координаты точки. Вычисление длины и направляющих косинусов вектора; координат вектора, заданного двумя точками; расстояния между точками.

25. Скалярное произведение векторов и его свойства. Выражение скалярного произведения через координаты векторов. Вычисление угла между векторами. Условие ортогональности векторов.

26. Векторное произведение векторов, его геометрический смысл и свойства. Выражение векторного произведения через координаты векторов. Условие коллинеарности векторов.

27. Смешанное произведение векторов, его геометрический смысл и свойства. Выражение смешанного произведения через координаты векторов. Условие компланарности векторов.

Раздел III. Аналитическая геометрия.

28. Понятие линии на плоскости. Общее уравнение линии и его нахождение по известному геометрическому свойству её точек. Окружность и её уравнение.

29. Прямая линия на плоскости и её общее уравнение. Нормальный и направляющий векторы прямой. Нахождение уравнения прямой, проходящей через точку перпендикулярно вектору. Построение прямой.

30. Каноническое уравнение прямой; уравнение прямой, проходящей через две точки; уравнение прямой с угловым коэффициентом; уравнение прямой в отрезках. Расстояние от точки до прямой на плоскости. Угол между прямыми на плоскости и его вычисление, условия 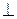 и ½ ½ прямых.

31. Понятие поверхности. Общее уравнение поверхности, его нахождение по известному геометрическому свойству её точек. Сфера и её уравнение.

32. Плоскость и её общее уравнение. Нормальный вектор плоскости. Уравнение плоскости, проходящей через точку перпендикулярно вектору. Построение плоскости.

33. Уравнение плоскости, проходящей через три точки; уравнение плоскости в отрезках. Расстояние от точки до плоскости. Угол между плоскостями, условия перпендикулярности и параллельности плоскостей.

34. Понятие линии в пространстве и её общее уравнение. Прямая линия в пространстве и её общее уравнение. Направляющий вектор прямой.

35. Уравнения прямой в пространстве: каноническое, проходящей через две точки; параметрическое. Приведение общего уравнения к каноническому.

36. Угол между двумя прямыми в пространстве, между прямой и плоскостью и их вычисление, условия перпендикулярности и параллельности двух прямых, прямой и плоскости. Точка пересечения прямой и плоскости.

37. Кривая 2-ого порядка на плоскости и её общее уравнение. Классификация кривых 2-ого порядка.

38. Эллипс. Каноническое уравнение эллипса. Построение эллипса. Вершины, полуоси, фокусы, эксцентриситет, общее геометрическое свойство точек эллипса.

39. Гипербола. Каноническое уравнение гиперболы. Построение гиперболы. Вершины, полуоси, фокусы, эксцентриситет, асимптоты, общее геометрическое свойство точек гиперболы.

40. Парабола. Каноническое уравнение параболы. Построение параболы. Вершина, фокус, эксцентриситет, директриса, общее геометрическое свойство точек параболы.

41. Область решений линейного неравенства, системы линейных неравенств в 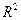. Графическое изображение области решений системы линейных неравенств в .

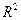⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: