 |
6.2. Краткие теоретические сведения.
|
|
|
|
Решение.
1а) Для построения области решений строим в системе координат  соответствующие заданным ограничениям-неравенствам граничные прямые:
соответствующие заданным ограничениям-неравенствам граничные прямые:  ,
,  ,
, 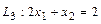 ,
,  ,
,  ,
,  . Прямая
. Прямая  проходит через точки
проходит через точки  и
и 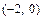 ;
;  - через точки
- через точки  и
и 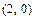 ;
;  - через точки
- через точки  и
и 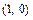 ;
;  совпадает с осью
совпадает с осью  ;
;  совпадает с осью
совпадает с осью  ;
; 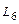 проходит через точку
проходит через точку  параллельно оси
параллельно оси  .
.
2а) Находим полуплоскости  ,
,  ,
, 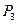 ,
,  ,
, 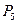 и
и  в которых выполняются неравенства. Для этого выбираем «пробную» точку и проверяем, удовлетворяет ли она ограничению-неравенству. Если удовлетворяет, то данное неравенство выполняется в полуплоскости, содержащей «пробную» точку. В противном случае берётся полуплоскость, не содержащая «пробной» точки. В качестве «пробной» точки выбирают любую точку, не принадлежащую граничной прямой, например, начало координат
в которых выполняются неравенства. Для этого выбираем «пробную» точку и проверяем, удовлетворяет ли она ограничению-неравенству. Если удовлетворяет, то данное неравенство выполняется в полуплоскости, содержащей «пробную» точку. В противном случае берётся полуплоскость, не содержащая «пробной» точки. В качестве «пробной» точки выбирают любую точку, не принадлежащую граничной прямой, например, начало координат 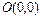 для нахождения полуплоскостей
для нахождения полуплоскостей  ,
,  ,
, 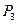 ,
,  . Полуплоскости, в которых неравенства выполняются, отмечаем стрелками, направленными внутрь данной полуплоскости.
. Полуплоскости, в которых неравенства выполняются, отмечаем стрелками, направленными внутрь данной полуплоскости.
3а) Строим область решений  как область, являющуюся пересечением полуплоскостей
как область, являющуюся пересечением полуплоскостей  , отмечая её штриховкой (см. рис. 4).
, отмечая её штриховкой (см. рис. 4).
Для решения задачи линейного программирования графическим способом: 1б) Строим нормальный вектор  прямой
прямой  , являющейся линией уровня целевой функции
, являющейся линией уровня целевой функции  . (вектор
. (вектор  показывает направление возрастания значений целевой функции).
показывает направление возрастания значений целевой функции).
2б) Перпендикулярно вектору  проводим пунктиром линию уровня
проводим пунктиром линию уровня 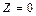 .
.
3б) Параллельным перемещением линии уровня 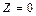 находим крайние точки области допустимых решений
находим крайние точки области допустимых решений  , в которых целевая функция достигает минимума – точку
, в которых целевая функция достигает минимума – точку  и максимума – точку
и максимума – точку 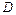 .
.
4б) Определяем координаты точек  и
и 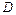 . Точку
. Точку  (точка пересечения прямых
(точка пересечения прямых  и
и  ) находим решая систему уравнений
) находим решая систему уравнений 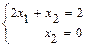 . Откуда
. Откуда  . Точку
. Точку 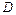 (точка пересечения прямых
(точка пересечения прямых  и
и  ) находим решая систему уравнений
) находим решая систему уравнений 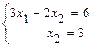 . Откуда
. Откуда  .
.
|
|
|
5б) Вычисляем:
 и
и  .
.

Рис. 4
Ответ: а ) Область  (см. рис. 4)
(см. рис. 4)
б); .
111-120. Имеются данные о работе трёх отраслей экономики в отчётном периоде и план выпуска конечной продукции  в следующем периоде (в усл. ден. ед. ). Требуется, используя модель Леонтьева многоотраслевой экономики, найти: а) матрицы коэффициентов прямых и полных затрат; б) плановые объёмы выпуска валовой продукции каждой из отраслей, межотраслевые поставки и объёмы выпуска чистой продукции. В ответе записать данные межотраслевого баланса планового периода. (Указание: значения коэффициентов прямых и полных затрат вычислить с точностью до 0. 01; значения плановых объёмов выпуска валовой и чистой продукции, межотраслевых поставок округлить до целых значений).
в следующем периоде (в усл. ден. ед. ). Требуется, используя модель Леонтьева многоотраслевой экономики, найти: а) матрицы коэффициентов прямых и полных затрат; б) плановые объёмы выпуска валовой продукции каждой из отраслей, межотраслевые поставки и объёмы выпуска чистой продукции. В ответе записать данные межотраслевого баланса планового периода. (Указание: значения коэффициентов прямых и полных затрат вычислить с точностью до 0. 01; значения плановых объёмов выпуска валовой и чистой продукции, межотраслевых поставок округлить до целых значений).
| Отрасли производства | Отрасти потребления | Конечный продукт | Валовой продукт | ||
| I | II | III | |||
| I | |||||
| II | |||||
| III | |||||
| Чистый продукт | |||||
| Валовой продукт | |||||
Решение.
1) Находим матрицу  коэффициентов прямых затрат
коэффициентов прямых затрат  (
( 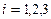 - номер отрасли производства,
- номер отрасли производства,  - номер отрасли потребления) и устанавливаем её продуктивность:
- номер отрасли потребления) и устанавливаем её продуктивность:
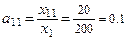 ,
,  ,
, 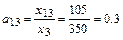
 ,
,  ,
, 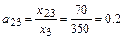
 ,
, 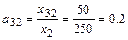 ,
,  .
.
Таким образом  .
.
Так как 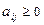 (
( 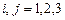 ) и
) и  , то матрица
, то матрица  продуктивна и, следовательно, для любого
продуктивна и, следовательно, для любого  существует решение
существует решение  уравнения Леонтьева:
уравнения Леонтьева:  , записываемое в виде
, записываемое в виде  , где
, где  - единичная матрица,
- единичная матрица, 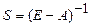 - матрица коэффициентов полных затрат,
- матрица коэффициентов полных затрат,  и
и  - векторы (матрицы-столбцы) валового выпуска и конечного продукта, соответственно.
- векторы (матрицы-столбцы) валового выпуска и конечного продукта, соответственно.
2а) Находим матрицу:
 .
.
3а) Находим матрицу 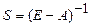 , обратную к
, обратную к 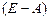 , методом присоединённой матрицы, по формуле:
, методом присоединённой матрицы, по формуле:  , где:
, где:

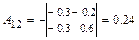
 ,
,


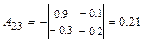 ,
,
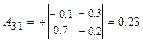

 ,
,
.
Тогда  .
.
1б) Находим вектор  валового выпуска на вектор
валового выпуска на вектор  конечного продукта в плановом периоде, следующим за отчётным (в предположении, что матрица
конечного продукта в плановом периоде, следующим за отчётным (в предположении, что матрица  , называемая также технологической, а, следовательно, и матрица
, называемая также технологической, а, следовательно, и матрица  не изменяются, т. е.
не изменяются, т. е.  ) по формуле:
) по формуле:
|
|
|
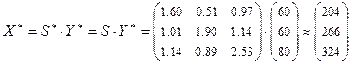 .
.
2б) Находим по формуле 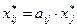 (
( 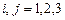 ) плановые межотраслевые поставки
) плановые межотраслевые поставки  , округляя полученные значения до целых (с учётом балансовых соотношений
, округляя полученные значения до целых (с учётом балансовых соотношений 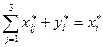 ,
, 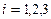 ):
):
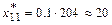 ,
,  ,
, 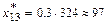 ,
,
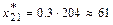 ,
, 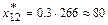 ,
,  ,
, 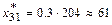 ,
,  ,
,  .
.
3б) Плановые объёмы 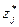
 выпуска чистой продукции каждой из отраслей находим по формуле
выпуска чистой продукции каждой из отраслей находим по формуле 
 :
:
 ,
,  ,
,
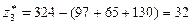 .
.
Ответ: Межотраслевой баланс планового периода имеет вид:
| Отрасли производства | Отрасти потребления | Конечный продукт | Валовой продукт | ||
| I | II | III | |||
| I | |||||
| II | |||||
| III | |||||
| Чистый продукт | |||||
| Валовой продукт | |||||
6. 2. Краткие теоретические сведения.
Тема 1. Определители.
Квадратной матрицей порядка  называется квадратная таблица из чисел
называется квадратная таблица из чисел  (
(  ,
, 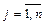 ):
):  , состоящая из
, состоящая из 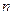 строк и
строк и 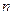 столбцов. У квадратной матрицы различают главную диагональ:
столбцов. У квадратной матрицы различают главную диагональ: 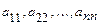 и побочную диагональ:
и побочную диагональ:  . Любой квадратной матрице
. Любой квадратной матрице  порядка
порядка 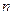 можно поставить в соответствие число
можно поставить в соответствие число 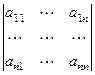 , равное алгебраической сумме
, равное алгебраической сумме  слагаемых, составленных определённым образом из элементов
слагаемых, составленных определённым образом из элементов 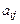 матрицы
матрицы 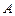 , называемое определителем матрицы. Кратко обозначается
, называемое определителем матрицы. Кратко обозначается 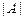 ,
,  .
.
Определителем 1-ого порядка называется число  .
.
Определителем 2-ого порядка называется число
 .
.
Определителем 3-его порядка называется число 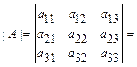
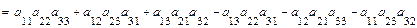 .
.
Минором элемента  называется определитель
называется определитель  , полученный из определителя
, полученный из определителя 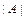 вычёркиванием
вычёркиванием  -ой строки и
-ой строки и  -ого столбца.
-ого столбца.
Алгебраическим дополнением  элемента
элемента  называется его минор
называется его минор  , взятый со знаком
, взятый со знаком  :
:
 .
.
Определителем порядка 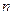 называется число
называется число
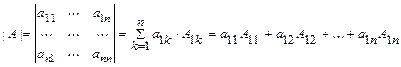
Разложением определителя 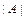 по
по  -ой строке (
-ой строке (  ) называется соотношение:
) называется соотношение:  .
.
Разложением определителя  по
по 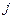 -ому столбцу (
-ому столбцу ( 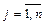 ) называется соотношение:
) называется соотношение: 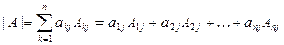
Определители обладают следующими свойствами:
1) определитель не изменится при замене всех его строк столбцами с теми же номерами;
2) определитель изменит знак на противоположный, если переставить местами любые две строки (два столбца) определителя;
3) общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя;
4) определитель равен нулю, если он содержит нулевую строку (столбец), две одинаковые или пропорциональные строки (столбца);
|
|
|
5) определитель не изменится, если к какой-либо строке (столбцу) прибавить другую строку (столбец), умноженную на любое число;
6) определитель треугольного вида (когда все элементы, лежащие по одну сторону одной из его диагоналей равны нулю) равен произведению диагональных элементов: 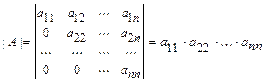 .
.
Тема 2. Матрицы.
Матрицей размера 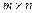 называется прямоугольная таблица из чисел
называется прямоугольная таблица из чисел  (
( 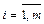 ,
, 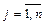 ):
): 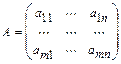 , состоящая из
, состоящая из  строк и
строк и  столбцов. Если необходимо указать размеры матрицы, то пишут
столбцов. Если необходимо указать размеры матрицы, то пишут 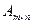 .
.
Если 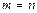 , то матрица
, то матрица  называется квадратной.
называется квадратной.
Нулевой называется матрица 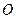 , все элементы которой равны нулю, например:
, все элементы которой равны нулю, например:  . Единичной называется квадратная матрица
. Единичной называется квадратная матрица 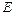 , на главной диагонали которой стоят единицы, а все остальные элементы равны нулю, например:
, на главной диагонали которой стоят единицы, а все остальные элементы равны нулю, например:  . Треугольной называется квадратная матрица
. Треугольной называется квадратная матрица  , все элементы которой расположенные по одну сторону от главной диагонали равны нулю, например:
, все элементы которой расположенные по одну сторону от главной диагонали равны нулю, например: 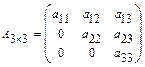 . Трапециевидной (ступенчатой) называется матрица
. Трапециевидной (ступенчатой) называется матрица 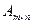
 , все элементы которой, расположенные ниже элементов
, все элементы которой, расположенные ниже элементов 
 равны нулю, например:
равны нулю, например:  .
.
Матрицы  и
и  называются равными и пишут
называются равными и пишут  , если они одинакового размера и их соответствующие элементы равны:
, если они одинакового размера и их соответствующие элементы равны: 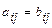 ,
, 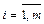 ,
, 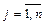 .
.
Матрицы можно транспонировать, складывать, вычитать, умножать на число, умножать на другую матрицу.
Транспонированной к матрице 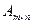 называется матрица
называется матрица  , столбцами которой являются соответствующие строки матрицы
, столбцами которой являются соответствующие строки матрицы 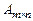 .
.
Суммой (разностью) матриц  и
и  одного размера
одного размера 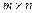 , называется матрица
, называется матрица  того же размера, для которой:
того же размера, для которой:
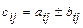 ,
, 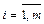 ,
, 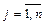 .
.
Произведением матрицы  размера
размера 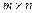 на число
на число 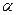 называется матрица
называется матрица  того же размера, для которой:
того же размера, для которой:  ,
, 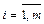 ,
, 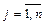 .
.
Линейной комбинацией матриц  и
и  одного размера
одного размера 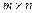 , называется матрица
, называется матрица  того же размера (
того же размера (  и
и 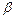 - произвольные числа), для которой:
- произвольные числа), для которой: 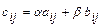 ,
, 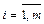 ,
, 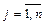 ,
,
Произведением матрицы  на матрицу
на матрицу  называется матрица
называется матрица 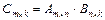 , каждый элемент которой
, каждый элемент которой  вычисляется по правилу:
вычисляется по правилу:
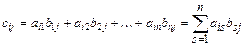 ,
,  ,
, 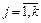 .
.
Операция умножения матрицы на матрицу определена не для всех матриц, а только для таких у которых число столбцов левой матрицы  равно числу строк правой матрицы
равно числу строк правой матрицы  . Такие матрицы называются согласованнымидля умножения. Поэтому прежде чем выполнять операцию умножения матрицы на матрицу следует проверить их согласованность для умножения и определить размерность матрицы-произведения (если умножение матриц возможно):
. Такие матрицы называются согласованнымидля умножения. Поэтому прежде чем выполнять операцию умножения матрицы на матрицу следует проверить их согласованность для умножения и определить размерность матрицы-произведения (если умножение матриц возможно): 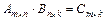 . Особенность операции умножения матриц состоит в том, что в общем случае:
. Особенность операции умножения матриц состоит в том, что в общем случае:  , т. е. переместительное свойство места не имеет.
, т. е. переместительное свойство места не имеет.
|
|
|
Элементарными преобразованиями матрицы называются:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число, отличное от нуля;
3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;
4) вычёркивание нулевой строки (столбца).
Матрицы  и
и  , полученные одна из другой в результате элементарных преобразований называются эквивалентными и пишут
, полученные одна из другой в результате элементарных преобразований называются эквивалентными и пишут  .
.
Обратной к квадратной матрице 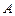 порядка
порядка  , называется матрица
, называется матрица  того же порядка, если:
того же порядка, если: 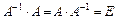 , где
, где  - единичная матрица порядка
- единичная матрица порядка  .
.
Квадратная матрица  называется невырожденной, если её определитель
называется невырожденной, если её определитель  . Обратная матрица всегда существует для невырожденных матриц.
. Обратная матрица всегда существует для невырожденных матриц.
Основными методами вычисления обратной матрицы являются:
Метод присоединённой матрицы. Если  -невырожденная матрица, то
-невырожденная матрица, то  , где
, где  - присоединённая матрица, для которой:
- присоединённая матрица, для которой: 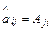
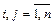 . Здесь
. Здесь  - алгебраические дополнения элементов
- алгебраические дополнения элементов 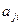 матрицы
матрицы  .
.
В частности, если  , то
, то 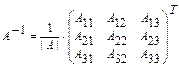
Метод элементарных преобразований. Для данной квадратной матрицы  порядка
порядка  строится прямоугольная матрица
строится прямоугольная матрица  размера
размера 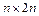 приписыванием к
приписыванием к  справа единичной матрицы. Далее, с помощью элементарных преобразований над строками, матрица
справа единичной матрицы. Далее, с помощью элементарных преобразований над строками, матрица 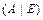 приводится к виду
приводится к виду 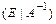 , что всегда возможно, если
, что всегда возможно, если  - невырожденная.
- невырожденная.
Матричными называются уравнения вида: 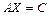 ,
, 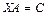 ,
,  ,
,
где матрицы 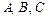 - известны, матрица
- известны, матрица  - неизвестна. Если квадратные матрицы
- неизвестна. Если квадратные матрицы  и
и  - невырожденные, то решения матричных уравнений записываются, соответственно, в виде:
- невырожденные, то решения матричных уравнений записываются, соответственно, в виде:  ,
, 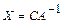 ,
,  .
.
Минором  -ого порядка матрицы
-ого порядка матрицы  размера
размера 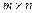 называется определитель
называется определитель 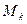 квадратной матрицы порядка
квадратной матрицы порядка  , образованной элементами матрицы
, образованной элементами матрицы  , стоящими на пересечении произвольно выбранных её
, стоящими на пересечении произвольно выбранных её  строк и
строк и  столбцов
столбцов  . Максимальный порядок
. Максимальный порядок 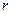 отличных от нуля миноров матрицы
отличных от нуля миноров матрицы  , называется её рангом и обозначается
, называется её рангом и обозначается 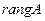 или
или 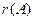 , а любой минор порядка
, а любой минор порядка 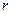 , отличный от нуля – базисным минором.
, отличный от нуля – базисным минором.
Тема 3. Системы линейных уравнений. Модель Леонтьева.
…Система уравнений вида: 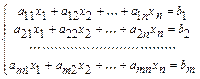 называется системой
называется системой  линейных уравнений с
линейных уравнений с 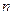 неизвестными. Числа
неизвестными. Числа  называются коэффициентами системы,
называются коэффициентами системы, 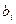 - свободными членами системы,
- свободными членами системы,  - неизвестными системы.
- неизвестными системы.
В матричной форме система имеет вид:  , где
, где  ,
,  ,
,  . Здесь
. Здесь  -матрица системы,
-матрица системы,  -матрица-столбец неизвестных,
-матрица-столбец неизвестных,  -матрица-столбец свободных членов.
-матрица-столбец свободных членов.
|
|
|
Если 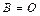 , то система называется однородной , в противном случае неоднородной.
, то система называется однородной , в противном случае неоднородной.
Система, матрица  которой является треугольной с диагональными элементами
которой является треугольной с диагональными элементами  , называется треугольной. Система, матрица
, называется треугольной. Система, матрица  которой является трапециевидной, называется трапециевидной.
которой является трапециевидной, называется трапециевидной.
Решением системы называется всякий упорядоченный набор чисел 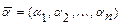 , обращающий каждое уравнение системы в равенство. Совокупность всех решений называется множеством решений системы.
, обращающий каждое уравнение системы в равенство. Совокупность всех решений называется множеством решений системы.
Система называется совместной, если она имеет, по крайней мере, одно решение; определённой, если она имеет только одно решение; неопределённой, если она имеет бесконечно много решений; несовместной, если она не имеет решений.
Однородная система уравнений всегда совместна, так как всегда имеет, по крайней мере, нулевое решение  . Треугольная система является определённой, трапециевидная система – неопределённой.
. Треугольная система является определённой, трапециевидная система – неопределённой.
Две системы называются эквивалентными, если множества их решений совпадают.
Элементарными преобразованиями систем уравнений называются:
1) перестановка уравнений;
2) перестановка местами слагаемых 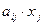 в каждом из уравнений системы;
в каждом из уравнений системы;
3) умножение уравнения на число, отличное от нуля;
4) прибавление к уравнению другого, умноженного на любое число;
5) вычёркивание уравнения вида: 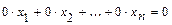 .
.
Основными точными методами решения систем линейных уравнений являются методы: Крамера, обратной матрицы и Гаусса.
Если число уравнений в системе  совпадает с числом неизвестных
совпадает с числом неизвестных  и определитель матрицы системы
и определитель матрицы системы  , то система имеет единственное решение, которое можно найти:
, то система имеет единственное решение, которое можно найти:
а) методом Крамера по формулам:  ,
, 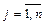 , где
, где  - определитель, получаемый из определителя матрицы системы
- определитель, получаемый из определителя матрицы системы  заменой
заменой 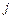 -ого столбца на столбец свободных членов;
-ого столбца на столбец свободных членов;
б) методом обратной матрицы по формуле 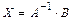 .
.
Методом Гаусса находят решение произвольной системы линейных уравнений. Метод состоит в приведении системы уравнений, с помощью элементарных преобразований, к системе специального вида, эквивалентной исходной, решение которой очевидно. Преобразования по методу Гаусса выполняют в два этапа. Первый этап называют прямым ходом, второй - обратным.
В результате прямого хода выясняют: совместна или нет система и если совместна то, сколько имеет решений - одно или бесконечно много, а также, в случае бесконечного множества решений, указывают базисные и свободные неизвестные для записи общего решения системы. Преобразования прямого хода выполняют, как правило, над расширенной матрицей системы 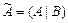 , которую получают, приписывая справа к матрице системы
, которую получают, приписывая справа к матрице системы  столбец свободных членов
столбец свободных членов  . В результате элементарных преобразований строк и перестановкой столбцов, матрица системы
. В результате элементарных преобразований строк и перестановкой столбцов, матрица системы  должна быть приведена к матрице
должна быть приведена к матрице  треугольного или трапециевидного вида с элементами
треугольного или трапециевидного вида с элементами 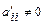 . При этом, система уравнений, матрица которой
. При этом, система уравнений, матрица которой  , является треугольной с диагональными элементами
, является треугольной с диагональными элементами 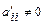
 , будет иметь единственное решение; система уравнений, матрица которой
, будет иметь единственное решение; система уравнений, матрица которой  , является трапециевидной с элементами
, является трапециевидной с элементами 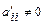
 , будет иметь бесконечно много решений. Если, при выполнении преобразований расширенной матрицы
, будет иметь бесконечно много решений. Если, при выполнении преобразований расширенной матрицы  , в преобразованной матрице
, в преобразованной матрице  появится строка
появится строка  , где
, где  , то это говорит о несовместности исходной системы уравнений. Базисные неизвестные указывают, выписывая базисный минор преобразованной матрицы системы
, то это говорит о несовместности исходной системы уравнений. Базисные неизвестные указывают, выписывая базисный минор преобразованной матрицы системы  . Базисными являются неизвестные преобразованной системы, столбцы коэффициентов
. Базисными являются неизвестные преобразованной системы, столбцы коэффициентов  при которых образуют базисный минор (определитель максимального порядка, отличный от нуля). Свободными являются неизвестные, не являющиеся базисными.
при которых образуют базисный минор (определитель максимального порядка, отличный от нуля). Свободными являются неизвестные, не являющиеся базисными.
В результате обратного хода находят решение системы, записывая его в виде общего решения, если их бесконечно много. Преобразования обратного хода часто выполняют, над уравнениями системы, соответствующей последней расширенной матрице  прямого хода. В случае единственного решения, его получают, находя последовательно значения всех неизвестных из уравнений системы, начиная с последнего. В случае, когда решений бесконечно много, их записывают в виде общего решения. Для этого свободным неизвестным придают разные произвольные постоянные значения:
прямого хода. В случае единственного решения, его получают, находя последовательно значения всех неизвестных из уравнений системы, начиная с последнего. В случае, когда решений бесконечно много, их записывают в виде общего решения. Для этого свободным неизвестным придают разные произвольные постоянные значения: 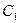 ,
,  , …,
, …, 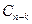 , и последовательно из уравнений системы, начиная с последнего, находят значения всех базисных неизвестных. Полученное решение называют общим. Придавая произвольным постоянным, конкретные значения, находят частные решения системы уравнений.
, и последовательно из уравнений системы, начиная с последнего, находят значения всех базисных неизвестных. Полученное решение называют общим. Придавая произвольным постоянным, конкретные значения, находят частные решения системы уравнений.
Уравнениямимежотраслевого баланса, описывающими процесс производства и потребления продукции  -отраслевой экономикой, называют уравнения
-отраслевой экономикой, называют уравнения 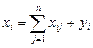 (
(  ), где
), где  - объём выпуска валовой продукции
- объём выпуска валовой продукции  -ой отраслью,
-ой отраслью,  - объём продукции
- объём продукции  -ой отрасли, потребляемый
-ой отрасли, потребляемый 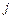 -ой отраслью для производства своей продукции,
-ой отраслью для производства своей продукции, 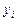 - объём выпуска конечной продукции
- объём выпуска конечной продукции  -ой отраслью, предназначенной для реализации в непроизводственной сфере.
-ой отраслью, предназначенной для реализации в непроизводственной сфере.
Если предположить, что 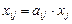 (гипотеза линейности), где
(гипотеза линейности), где 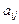 - постоянные числа, характеризующие технологию производства (показывают затраты продукции
- постоянные числа, характеризующие технологию производства (показывают затраты продукции  -ой отрасли на производство 1 единицы продукции
-ой отрасли на производство 1 единицы продукции 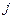 -ой отрасли) и называемые коэффициентами прямых затрат, то уравнения межотраслевого баланса запишутся в виде:
-ой отрасли) и называемые коэффициентами прямых затрат, то уравнения межотраслевого баланса запишутся в виде:  (
(  ). Их называют уравнениями линейного межотраслевого баланса или линейной моделью Леонтьева многоотраслевой экономики и записывают, как правило, в матричном виде:
). Их называют уравнениями линейного межотраслевого баланса или линейной моделью Леонтьева многоотраслевой экономики и записывают, как правило, в матричном виде: 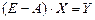 , где
, где  - единичная матрица;
- единичная матрица;  - матрица коэффициентов прямых затрат;
- матрица коэффициентов прямых затрат;  и
и 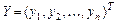 - векторы (матрицы-столбцы) валового и конечного продукта, соответственно.
- векторы (матрицы-столбцы) валового и конечного продукта, соответственно.
Основная задача линейного межотраслевого баланса состоит в отыскании вектора  , который при известной ма
, который при известной ма
|
|
|


