 |
а)длину стороны ; б)уравнение стороны ;
|
|
|
|
.
Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы, с учётом перестановки местами столбцов, образуют первый и второй столбцы коэффициентов при неизвестных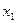 
и 
: 
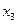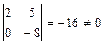. Поэтому выбираем в качестве базисных – неизвестные 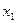и 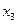, тогда свободными будут неизвестные 
и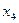 
.
3б) Выполняем обратный ход метода Гаусса.
Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: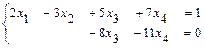 
. Свободным неизвестным придаём разные, произвольные постоянные значения: 
, 
, и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных: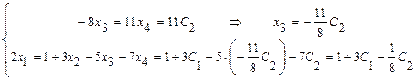 
.
Тогда общее решение системы запишется в виде:
4б) Выполняем проверку:
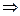
Ответ: .
в).
Решение.
1в) Записываем расширенную матрицу системы:
.
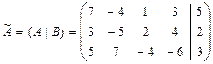2в) Выполняем прямой ход метода Гаусса.
.
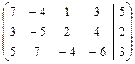
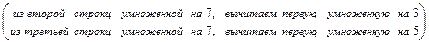
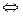
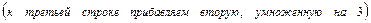
При выполнении преобразования расширенной матрицы 
, в преобразованной матрице 
появилась строка 
, соответствующая уравнению 
, которому не удовлетворяет ни один набор значений неизвестных 
, что говорит о несовместности исходной системы уравнений.
Ответ: Система несовместна.
51 – 60. Исследовать квадратичную форму на знакоопределённость (по критерию Сильвестра).
а) 
; б) 
Решение.
1а) Записываем матрицу квадратичной формы: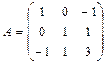 
.
2а) Проверяем является ли матрица 
невырожденной. Для этого вычисляем её определитель 
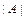и проверяем, равен ли он нулю: 
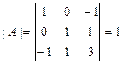. Так как 
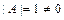, то матрица - невырожденная и, следовательно, для исследования квадратичной формы на знакоопределённость можно применить критерий Сильвестра.
|
|
|
3а) Вычисляем угловые миноры матрицы и делаем вывод о знакоопределённости квадратичной формы: 
, 
, 
. Так как выполняется условие: 
, 
, 
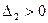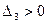, то по критерию Сильвестра квадратичная форма положительно определена.
Ответ: Квадратичная форма положительно определена.
1б) Записываем матрицу квадратичной формы: 
.
2б) Вычисляем её определитель 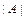и проверяем, равен ли он нулю: 
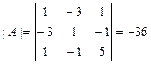. Так как 
, то матрица - невырожденная и, следовательно, для исследования квадратичной формы на знакоопределённость можно применить критерий Сильвестра.
3б) Вычисляем угловые миноры матрицы и делаем вывод о знакоопределённости квадратичной формы: , 
, 
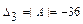. Так как два угловых минора нечётного порядка имеют разные знаки: , 
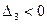, то по критерию Сильвестра квадратичная форма знакопеременна.
Ответ: Квадратичная форма знакопеременна.
61 – 70. Даны векторы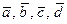 
: 
; 
; 
; 
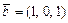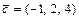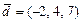. Требуется: а) вычислить скалярное произведение векторов 
, если 
, 
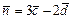; б) вычислить векторное произведение векторов 
; в) показать, что векторы 
образуют базис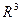 
и найти координаты вектора 
в этом базисе.
Решение.
1a). Находимвектор
=.
2а) Находимвектор
=.
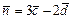
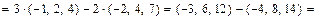
3а) Вычисляем скалярное произведениевекторов :
.
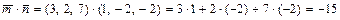б) Вычисляем векторное произведение векторов :
= 
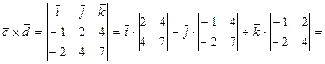
1в) Покажем, что векторы 
образуют базис 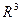. Для этого составим определитель, столбцами которого являются координаты этих векторов и покажем, что он отличен от нуля.
.
Так как 
, то векторы образуют базис 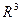и, следовательно, вектор 
единственным образом можно разложить по векторам этого базиса.
2в) Записываем разложение вектора по векторам базиса 
:
или 
.
Коэффициенты разложения 
, 
, 
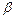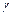называют координатами вектора в базисе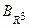 
и записывают: 
.
|
|
|
3в) Записываем векторное уравнение относительно , , 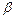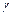в виде эквивалентной ему системы линейных уравнений: 
, и находим единственное решение системы, например, по формулам Крамера:
, где
, 
, 
, 
.
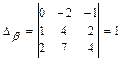Таким образом: 
, 
, 
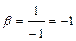. Следовательно, разложение имеет вид: 
или кратко: 
.
Ответ: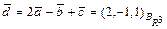 
.
71-80. Даны вершины треугольника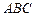 
: 
, 
, 
Требуется найти:
а)длину стороны; б)уравнение стороны;
|
|
|
