 |
Рис.5 Рис 6. Рис. 9а Рис. 9б. 3а) - уравнение параболы с вершиной в точке и осью симметрии, параллельной координатной оси (рис
|
|
|
|
Рис. 5 Рис 6
2) 
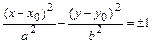- уравнения гипербол (называемых сопряжёнными) с центром в точке 
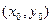и осями симметрии, параллельными координатным осям. Числа 
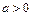и 
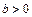- называются полуосями гипербол; прямоугольник со сторонами 
, 
параллельными осям симметрии и центром в точке 
- основным прямоугольником гипербол; точки пересечения основного прямоугольника с осями симметрии - вершинами гипербол; прямые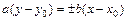 
, проходящие через противоположные вершины основного прямоугольника – асимптотами гипербол.
Для построения гиперболы в системе координат 
: 1) отмечаем центр гиперболы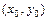 
; 2) проводим через центр 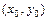пунктирной линией оси симметрии гиперболы; 3) строим пунктиром основной прямоугольник гиперболы с центром 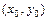и сторонами и 
параллельными осям симметрии; 4) проводим через противоположные вершины основного прямоугольника пунктирной линией прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко, при бесконечном удалении от начала координат, приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы 
(рис. 7) или гиперболы 
(рис. 8).
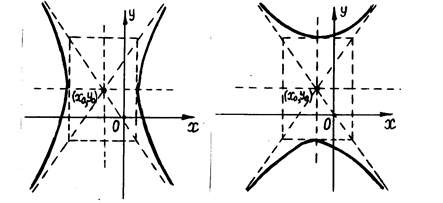
Рис. 7 Рис. 8
3а)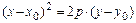 
- уравнение параболы с вершиной в точке 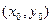и осью симметрии, параллельной координатной оси 
(рис. 9).
3б)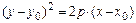 
- уравнение параболы с вершиной в точке 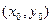и осью симметрии, параллельной координатной оси 
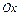(рис. 10).
Для построения параболы в системе координат : 1) отмечаем вершину параболы 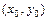; 2) проводим через вершину 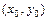пунктирной линией ось симметрии параболы; 3) изображаем сплошной линией параболу, направляя её ветвь, с учётом знака параметра параболы 
: при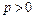 
- в положительную сторону координатной оси, параллельной оси симметрии параболы (рис. 9а и 10а); при 
- в отрицательную сторону координатной оси (рис. 9б и 10б).
|
|
|
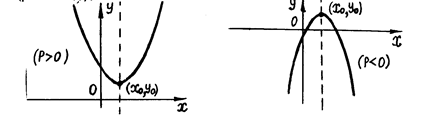
Рис. 9а Рис. 9б
Рис. 10а Рис. 10б
Тема 10. Системы линейных неравенств. Линейные задачи оптимизации.
Линейным неравенством называют неравенство вида: , где - некоторые числа, - координаты точки пространства. Совокупность всех точек, координаты которых удовлетворяют неравенству, называют областью решений данного неравенства.
Для пространства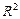 
линейное неравенство имеет вид 
. Его областью решений является одна из полуплоскостей, на которые граничная прямая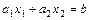 
делит плоскость 
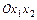. Для того, чтобы установить какая из полуплоскостей удовлетворяет данному неравенству выбирают «пробную» точку и проверяют, удовлетворяет ли она ограничению-неравенству. Если удовлетворяет, то неравенство выполняется в полуплоскости, содержащей «пробную» точку, в противном случае берётся другая полуплоскость. В качестве «пробной» точки выбирают любую точку, не принадлежащую граничной прямой. Полуплоскость, в которой неравенство выполняется, отмечают стрелками, направленными внутрь данной полуплоскости.
Системой линейных неравенств называют систему неравенств вида:
,
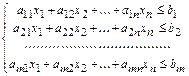где 
- коэффициенты системы,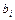 
- свободные члены системы. Совокупность всех точек 
, координаты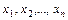 
которых удовлетворяют каждому из неравенств, называют областью решенийсистемы неравенств.
Для пространства 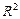система линейных неравенств имеет вид
.
Её областью решений является пересечение полуплоскостей, ограниченных прямыми, уравнения которых получают из неравенств заменой в них знаков неравенств на знаки равенств
|
|
|
Линейное программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения. Задачи линейного программирования (ЗЛП) являются задачами оптимизации и широко применяются для решения экономических задач.
Существует несколько форм записи задачи линейного программирования.
Общей задачей линейного программирования называют задачу:
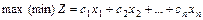
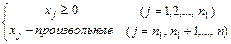
Симметричной задачей линейного программирования называют задачу:
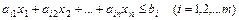
или 
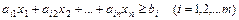
Канонической задачей линейного программирования называют задачу:
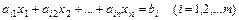
Функция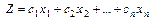 
называется целевой функцией; величины 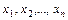называются переменными задачи; система уравнений и неравенств, которым удовлетворяют переменные задачи называется системой ограничений; любой 
-мерный вектор 
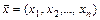удовлетворяющий системе ограничений называется допустимым решением ( планом ) задачи линейного программирования; множество всех допустимых решений называется областью допустимых решений; допустимое решение ЗЛП, при котором целевая функция достигает экстремума называется оптимальным решением ( оптимальным планом ) задачи линейного программирования.
Все формы записи ЗЛП эквивалентны. ЗЛП с двумя переменными может быть решена графическим методом, который основан на возможности графического изображения области допустимых решений задачи и нахождения среди них оптимального решения. Область допустимых решений ЗЛП строится как пересечение областей решений каждого из ограничений, входящих в систему ограничений задачи. Для нахождения среди допустимых решений оптимального решения используют линии уровня целевой функции. Линией уровня целевой функции называется прямая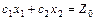 
, на которой целевая функция принимает постоянное значение 
. Все линии уровня параллельны между собой. Их нормаль 
показывает направление наибольшего возрастания значений целевой функции, а вектор ( 
) – направление наибольшего убывания.
Если построить на одном рисунке область допустимых решений, вектор 
( ) и одну из линий уровня, например 
, то задача линейного программирования сводится к определению в области допустимых решений точки в направлении вектора ( ), через которую проходит линия уровня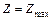 
( 
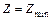), соответствующая наибольшему (наименьшему) значению функции 
. В этом и состоит графический метод решения ЗЛП.
|
|
|
Примером экономической задачи, сводящейся к задаче линейного программирования, является задача оптимального использования ресурсов.
При производстве видов продукции используется 
видов ресурсов. Известны: 
- запасов ресурсов; ( 
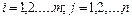) - расход 
-ого вида ресурса на производство одной единицы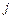 
-ого вида продукции; 
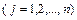- прибыль, получаемая от реализации одной единицы 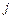-ого вида продукции. Требуется составить план выпуска продукции 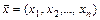, где 
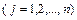- объём выпуска 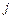-ой продукции, который обеспечивает максимальную прибыль . Математическая модель такой задачи имеет вид:
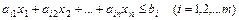
и является задачей линейного программирования.
|
|
|
