Главная | Обратная связь | Поможем написать вашу работу!

Получение частотных характеристик динамических звеньев и систем

При получении частотных характеристик входной сигнал звена рассматривается в форме x ₁(t)=sinw t, то есть принимается изменяющимся по синусоидальному закону с амплитудой А =1 и фазой j=0 (рис. 16). Значения частоты w рассматриваются в диапазоне от -¥ до +¥. Отрицательные частоты здесь вводятся для удобства построения математического аппарата анализа систем. На практике характеристики получают для частот в диапазоне от 0 до +¥. В область отрицательных частот их распространяют в соответствии со свойствами четности или нечетности. Следует помнить, что аналитические выражения для частотных характеристик принято записывать, подразумевая значение аргумента w³0.

Рис. 16.

Известно, что, преобразуя гармонический сигнал, линейное звено может изменить его амплитуду и фазу. Частота сигнала сохраняется. Степени изменения амплитуды и фазы определяются динамическими свойствами звена и зависят от частоты преобразуемого сигнала. Эти эффекты отражаются двумя главными частотными характеристиками – амплитудно-частотной и фазо-частотной.

Амплитудно-частотная характеристика (АЧХ)A(w) показывает степень усиления или ослабления звеном амплитуды пропускаемого гармонического сигнала в зависимости от его частоты.

Фазо-частотная характеристика (ФЧХ)j(w) показывает зависимость от частотыфазового сдвига, вносимого звеном в пропускаемый гармонический сигнал.

Формально АЧХ и ФЧХ могут быть получены на основе частотной передаточной функции (ЧПФ) звена .

ЧПФ может быть получена из обычной передаточной функции заменой оператора Лапласа s на : |_s₌_j _w.

ЧПФ представляет собой комплексную функцию, то есть каждому фиксированному значению w=w₁, соответствует значение ЧПФ , в общем случае являющееся комплексным числом W ₁= a+jb = re^j ^j, где а –вещественная часть, b– мнимая часть, – модуль числа W ₁, j=arg(W ₁)=arctg(b/a) – аргумент числа W ₁ (рис. 17).

Рис. 17.

Как и комплексное число, ЧПФ может быть представлена в алгебраической (через вещественную и мнимую части) и показательной (через модуль и аргумент) формах:

где U (w) и V (w) – соответственно вещественная и мнимая части ЧПФ, A (w) и j(w) – соответственно модуль и аргумент ЧПФ.

АЧХ определяется как модуль ЧПФ: . Модуль, как известно, является четной функцией.

ФЧХ определяется как аргумент ЧПФ: . Аргумент – нечетная функция.

По аналогии с комплексным числом для АЧХ и ФЧХ можно записать соотношения:

, (3.1)

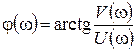, (3.2)

но пользоваться этими соотношениями для получения характеристик динамических звеньев и систем не рекомендуется. Причины этого покажет следующий пример.

Пример 3.1. Получить АЧХ и ФЧХ динамического звена, описываемого уравнением

Построить их примерные графики.

Используя взаимно-однозначную связь дифференциального уравнения и передаточной функции, запишем ее:

Теперь можно было бы перейти к ЧПФ:

и заняться выделением ее вещественной и мнимой частей, чтобы воспользоваться соотношениями (3.1) и (3.2). Но преобразования будут весьма трудоемкими, а итоговое выражение вида (3.1) – неоправданно сложным и явно неудобным для дальнейшего использования.

Кроме того, при получении j(w) в форме (3.2) следует помнить, что математическая функция arctg x имеет бесконечное множество значений:

arctg x =Аrctg x ± n p,

где Аrctg x – главное значение, лежащее в диапазоне от -p/2 до +p/2; n =0,1,2,… С формальной точки зрения все эти значения равноценны. Такая трактовка результата неприемлема при получении ФЧХ, так как последняя должна однозначно характеризовать свойства реального объекта, моделью которого является передаточная функция.

Для устранения неоднозначности и значительного упрощения процедуры получения АЧХ и ФЧХ необходимо использовать следующий способ.

Передаточная функция должна быть представлена в форме дроби вида

, (3.3)

где z_i – вещественные константы или полиномы относительно s первой или второй степени.

При отсутствии комплексных корней относительно s у числителя и знаменателя W (s) они должны быть разложены на сомножители, содержащие s впервой степени. Один из сомножителей в числителе окажется вещественной константой (коэффициент передачи звена k).

Только при наличии комплексных корней относительно s у числителя или знаменателя W (s) сомножитель z_i оставляют в форме полинома второй степени относительно s, соответствующего такой паре корней.

При выполнении указанных требований ЧПФ будет иметь аналогичный вид:

, (3.4)

где z_i – комплексные функции , например .

Теперь АЧХ и ФЧХ можно определить на основе правил умножения и деления комплексных чисел:

1. Модуль произведения равен произведению модулей сомножителей.

2. Модуль отношения равен отношению модулей числителя и знаменателя.

3. Аргумент произведения равен сумме аргументов сомножителей.

4. Аргумент отношения равен разности аргументов числителя и знаменателя.

Соответственно для ЧПФ вида (3.4) получим:

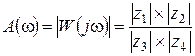Разложим на сомножители передаточную функцию из примера 3.1:

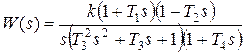перейдем к ЧПФ

Теперь, учитывая достаточно простые и однозначные выражения для модулей и аргументов сомножителей в числителе и знаменателе ЧПФ, составим выражения для АЧХ и ФЧХ:

Построение примерных графиков выполняется сначала для положительных частот. Для примерных графиков необходимо правильно определить их поведение для и , после чего приближенно спрогнозировать их поведение на промежуточных частотах, прежде всего, установить возможность резонансного пика на АЧХ.

Рассмотрим выражение для АЧХ и получим:

Если представить квадратный трехчлен в знаменателе передаточной функции в форме

получим то есть высота резонансного пика будет незначительной [1], и его можно не учитывать. Следовательно, можно прогнозировать монотонный характер графика АФХ.

Для построения графика на отрицательных частотах учтем, что АЧХ – четная функция (рис. 18а).

Рис. 18.

Рассмотрим выражение для ФЧХ и получим:

В зависимости от соотношения постоянных времени рассматриваемого звена можно прогнозировать различные варианты характера графика ФЧХ на промежуточных частотах:

1 – если T ₁ значительно превосходит остальные постоянные времени по величине;

2 – если T ₁ значительно меньше остальных постоянных времени;

3 – во всех остальных случаях.

Для построения графика на отрицательных частотах учтем, что ФЧХ – нечетная функция (рис. 18б).

Амплитудно-фазовой частотной характеристикой (амплитудно-фазовой характеристикой, АФХ) называется годограф частотной передаточной функции.

Годограф комплексной функции одного вещественного аргумента строится на комплексной плоскости, как показано на рис. 19. Любому значению аргумента на комплексной плоскости соответствует точка. Множество точек, соответствующее плавному изменению аргумента от - ¥ до + ¥, образует кривую, которая и называется годографом.

Рис. 19.

Пусть задана ЧПФ W (j w). Для некоторой частоты w₁ (для определенности w₁> 0) соответствующая точка на комплексной плоскости может быть построена в декартовых координатах на основе представления ЧПФ в алгебраической форме: W (j w₁)= U (w₁)+ jV (w₁), где U (w₁) – значение ВЧХ, V (w₁) – значение МЧХ на частоте w₁.

Представление ЧПФ в показательной форме даёт полярные координаты такой точки:

где – значение АЧХ, – значение ФЧХ частоте .

Для получения второй половины годографа, соответствующей отрицательным частотам, определим положение изображающей точки для на основе свойств четности и нечетности частотных характеристик.

ВЧХ является четной функцией, следовательно, при изменении знака аргумента горизонтальная координата изображающей точки сохраняет свое значение 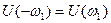. МЧХ – нечетная функция, следовательно, при изменении знака  изменяется знак вертикальной координаты изображающей точки .

Таким образом, точки годографа, соответствующие частотам и , симметричны относительно горизонтальной оси. Поскольку значение выбиралось произвольным, такой вывод можно сделать в целом об участках АФХ, соответствующих w > 0 и w < 0. Участок соответствующий w < 0, принято показывать пунктирной линией.

Итак, АФХ может быть построена двумя способами: с использованием ВЧХ и МЧХ (декартовых координат) или с использованием АЧХ и ФЧХ (полярных координат). При правильном построении оба способа должны давать одинаковый результат.

Точное построение АФХ требует численного расчета. Однако для решения практических задач, как правило, можно ограничиться приближенным построением АФХ вручную с точным расчетом отдельных точек.

Требования к приближенному построению АФХ:

1. Построение подробно выполняется для . Для отрицательных частот вторая половина АФХ строится с учетом ее симметрии относительно горизонтальной оси. Ее принято изображать пунктирной линией.

2. Должны быть определены квадранты, в которых проходит АФХ.

3. Должны быть найдены и указаны точки АФХ, соответствующие частотам и . При отсутствии таких точек (асимптотический характер кривой) должны быть найдены соответствующие асимптоты и правильно показан вид участков, соответствующих и .

4. Должны быть найдены и указаны частоты, соответствующие точкам пересечения АФХ с осями координат, и координаты таких точек.

5. Направление увеличения частоты указывается на АФХ стрелкой.

Пример 3.2. Построить АФХ интегрирующего звена с замедлением.

Его передаточные функции:

; .

Выражения для АЧХ и ФЧХ имеют вид:

, .

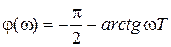Их графики показаны на рис. 20.

Рис. 20.

По АЧХ и ФЧХ можно установить следующее:

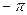- при w > 0 значения ФЧХ лежат в пределах от до , следовательно, АФХ при w > 0 лежит в третьем квадранте, точек пересечения АФХ с осями координат нет;

- при длина вектора, направленного в точки АФХ, стремится к бесконечности, угол наклона -к значению 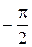, следовательно, АФХ уходит вниз в бесконечность (при этом степень ее удаления от вертикальной оси установить не удается);

- при A (w) = 0, , следовательно АФХ стремится в начало координат вдоль горизонтальной оси;

- длина вектора направленного в точки АФХ, и угол его наклона изменяются монотонно.

Варианты АФХ, соответствующие полученным результатам (с учетом неопределенности при ), показаны на рис. 21.

Рис. 21.

Дополнительную информацию, позволяющую уточнить поведение АФХ на малых частотах, можно получить по ВЧХ и МЧХ. Получим выражения для этих характеристик и построим примерные графики (рис. 22):

, .

Рис. 22.

По графику и из соответствующего выражения нетрудно установить, что горизонтальная координата точек АФХ при стремится к значению –kT. Следовательно, правильная АФХ для данного примера – кривая 2 на рисунке 21. Причем асимптотой АФХ при и является вертикальная прямая, пересекающая горизонтальную ось в точке с координатой –kT.

Отметим, что попытка выполнить приближенное построение АФХ по ВЧХ и МЧХ также вызовет затруднения: по их графикам не удается установить асимптотический характер АФХ при (характеристика приходит в начало координат вдоль горизонтальной оси).

Таким образом, при приближенном построении АФХ целесообразно использовать обе пары частотных характеристик: АЧХ и ФЧХ, ВЧХ и МЧХ – для получения полной информации или, по крайней мере, для проверки результата.

Пример 3.3. Построить АФХ звена с передаточной функцией

Перейдем к ЧПФ звена:

Выражения для АЧХ и ФЧХ имеют вид:

, .

Их графики показаны на рис. 23.

По АЧХ и ФЧХ можно установить следующее:

- частоте соответствует точка с координатой k на положительной вещественной полуоси;

- при увеличении частоты длина вектора монотонно уменьшается, при АФХ приходит в начало координат;

Рис. 23.

- при w > 0 с ее увеличением угол наклона вектора монотонно изменяется от 0 до , следовательно, АФХ последовательно проходит три квадранта в отрицательном направлении и приходит в начало координат вдоль вертикальной оси;

- при w>0 АФХ последовательно пересекает вертикальную и горизонтальную оси.

АФХ показана на рис. 24.

Рис. 24.

Рассчитаем точки пересечения АФХ с осями координат для w > 0.

Точке пересечения АФХ с вертикальной осью соответствует уравнение:

откуда

, ; .

Расстояние от начала координат до рассматриваемой точки равно

Точке пересечения АФХ с горизонтальной осью соответствует уравнение:

откуда

, ; .

Расстояние от начала координат до рассматриваемой точки равно

Теперь воспользуемся второй парой характеристик:

;

, .

Их графики (рис. 25) не противоречат построенной выше АФХ.

Рис. 25.

Точке пересечения АФХ с вертикальной осью соответствует уравнение:

, ,

откуда .

Вертикальная координата этой точки:

Точке пересечения АФХ с горизонтальной осью соответствует уравнение:

откуда .

Горизонтальная координата этой точки:

Результаты совпадают с полученными выше.

Контрольные вопросы и задачи для самостоятельной работы

1. Какие свойства динамического звена отражают АЧХ и ФЧХ. Рассмотрите примеры передаточных функций динамических звеньев и сформулируйте выводы об их динамических свойствах по этим характеристикам.

2. Перечислите взаимные связи частотных характеристик.

3. Как проявляются свойства симметрии для АЧХ, ФЧХ, ВЧХ, МЧХ, АФХ? Дайте обоснование.

4. Отображая значения комплексных функций на комплексной плоскости (рис. 17) получите самостоятельно выражения для модулей и аргументов возможных сомножителей ЧПФ:

а) z ₁ =k; б) z ₂= s; в) z ₃=1+ Ts; г) z ₄=1 -Ts; д) z ₅=1+ T ² s ²;

е) 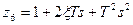; ж) ; з) .

Для пунктов д-ж необходимо отдельно рассмотреть интервалы частот и .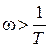

5. Получите выражение для АЧХ колебательного звена с передаточной функцией , . Из условия найдите частоту резонанса, диапазон значений коэффициента демпфирования , для которого резонансный пик на графике АЧХ существует и высоту этого пика.