Анализ устойчивости линейных стационарных систем

(алгебраические методы)

Устойчивость линейной системы полностью определяется ее характеристическим полиномом, который представляет собой знаменатель передаточных функций замкнутой системы.

Для устойчивости системы необходимо и достаточно, чтобы все корни характеристического полинома лежали в левой полуплоскости комплексной плоскости: , i= 1,2,…, n.

Из этого условия вытекает значительно более удобное для использования необходимое условие устойчивости: все коэффициенты характеристического полинома должны иметь одинаковый знак: a_i> 0, i= 0,1,…, n. Формально допускается и a_i< 0, i= 0,1,…, n. Это условие является и достаточным для систем первого и второго порядка. Для систем более высокого порядка при выполнении необходимого условия вопрос об устойчивости остается открытым и для ответа на него требуется дополнительно применить один из критериев устойчивости, выполняющих роль достаточных условий.

С проверки выполнения необходимого условия всегда должен начинаться анализ устойчивости.

Пример 6.1. Проанализировать устойчивость систем с характеристическими полиномами:

а) ,

б) ,

в) ;

г)

В случае «а» необходимое условие устойчивости не выполняется (a ₂=0) – система не является устойчивой.

В случае «б» выполнены необходимое и достаточное условия – система устойчива.

В случае «в» необходимое условие устойчивости выполнено, но для окончательного вывода об устойчивости необходимо продолжить анализ.

В случае «г» знак одного из коэффициентов отличается от остальных - система неустойчива.

Пример 6.2. Проанализировать устойчивость системы, заданной структурно-динамической схемой на рис. 51а.

Рис. 51.

Для получения характеристического полинома необходима передаточная функция замкнутой системы. Для ее получения преобразуем структурную схему, как было показано на предыдущем практическом занятии (рис. 51б).

Теперь последовательно (рис. 52а,б) заменяя участки типового соединения звеньев результирующими передаточными функциями, получим основную передаточную функцию системы и характеристический полином:

Рис. 52.

, , ,

,

,

, , .

Для системы второго порядка необходимое условие устойчивости является и достаточным. Коэффициенты a ₀ и a ₂ всегда положительны. Требование положительности a ₁ дает условие устойчивости рассматриваемой системы:

,

.

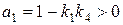Алгебраический критерий устойчивости Гурвица предусматривает работу с матрицей, составленной из коэффициентов характеристического полинома D (s) по следующим правилам:

- матрица квадратная размерностью ;

- главная диагональ заполняется коэффициентами, начиная с a ₁ в порядке возрастания;

- в строки с нечетными номерами заносятся коэффициенты с нечетными номерами в порядке возрастания;

- в строки с четными номерами заносятся коэффициенты с четными номерами, начиная с , в порядке возрастания;

- коэффициенты в строках располагают вблизи главной диагонали, остальные элементы матрицы, принимают равными нулю:

.

При положительном коэффициенте для устойчивости системы достаточно, чтобы все определители Гурвица были положительны: . При a ₀<0 определитель должны быть отрицательны.

Определители Гурвица – это угловые определители рассматриваемой матрицы, получаемые по известным правилам:

, , , …

Соответственно определитель получают, отбрасывая n -й столбец и n -ю строку матрицы; определитель соответствует всей матрице.

Отметим следующие свойства определителей Гурвица:

1. Если выполнено необходимое условие устойчивости, то всегда .

2. При раскрытии по последнему столбцу получим, , так как кроме a_n все элементы данного столбца равны нулю. Если выполнено необходимое условие устойчивости, то . Следовательно, знак совпадает со знаком , и отдельно проверять его также не требуется.

В результате применение критерия Гурвица сводится к проверке n -2 неравенств, получаемых на основе определителей с по .

Признаком нахождения системы на границе устойчивости является равенство нулю последнего определителя (). С учетом соотношения это может быть вызвано равенством нулю любого из сомножителей. Доказано, что при a_n= 0 имеет место апериодическая граница устойчивости, при – колебательная граница устойчивости.

Рассмотрим примеры задач анализа и синтеза систем управления, решение которых возможно с использованием критерия Гурвица.

Проверка устойчивости системы

Пример 6.3. Рассмотрим замкнутую систему (рис. 53) с параметрами: k =20; Т ₁=0,1; Т ₂=0,02.

Рис. 53.

Составим характеристический полином:

,

D (s) =R (s) +Q (s) =T ₂ s ³ +s ² +kT ₁ s+k,

a ₀ =T ₂, a ₁ = 1, a ₂ =kT ₁, a ₃ =k.

и матрицу коэффициентов: .

Проверим второй определитель Гурвица:

.

Вывод: система устойчива.

Определение критического значения коэффициента передачи

Критическим называется такое значение коэффициента передачи разомкнутой системы, при котором замкнутая система находится на границе устойчивости.

Пример 6.4. Рассмотрим замкнутую систему (рис. 54) с параметрами: T ₁ = 0,1; T ₂ = 0,2.

Рис.54.

Составим характеристический полином:

D (s) =T ₁ T ₂ s ³ + (T ₁ +T ₂) s ² +s+k.

Для рассматриваемой системы a_n=a ₃ =k. Значение k =0, формально обеспечивающее апериодическую границу устойчивости, рассматривать не имеет смысла.

Колебательная граница устойчивости может быть достигнута при . Составим этот определитель:

.

Приравнивая полученное выражение к нулю, найдем критическое значение коэффициента передачи:

.

Определение условий устойчивости

Условия устойчивости получают в виде неравенств относительно параметров системы, при выполнении которых системы является устойчивой. Если неравенство включает в себя коэффициент передачи k, его обязательно решают относительно k, то есть приводят к форме ограничения на величину коэффициента передачи системы.

Вернемся к примеру 6.4 и решим неравенство :

T ₁ +T ₂– kT ₁ T ₂ > 0.

В результате условие устойчивости получаем в форме

.

Пример 6.5. Получим условие устойчивости для системы, показанной на рис. 55.

Рис.55.

Составим характеристический полином:

D (s) =T ₂ s ⁴ +s ³ +kT ₁² s ² + 2 kT ₁ s+k.

Поскольку порядок системы n= 4, в соответствии с критерием Гурвица требуется рассматривать два определителя:

,

.

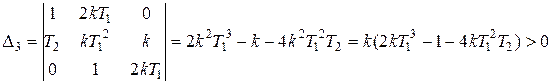Из первого неравенства получим: T ₁>2 T ₂.

Из второго неравенства: .

С учетом первого неравенства найдем ограничение на величину коэффициента передачи:

.

Ответ получен в виде двух неравенств.

Отметим, что в данном примере получено ограничение на величину коэффициента передачи снизу. Таким образом, структура рассмотренной системы такова, что при обеспечении значений параметров, удовлетворяющих полученным условиям, она будет устойчива. Но при снижении величины коэффициента передачи может утратить устойчивость (при ). Устойчивую линейную систему, которая может утратить устойчивость за счет снижения коэффициента передачи, называют условно устойчивой. Все остальные устойчивые линейные системы называют абсолютно устойчивыми.

Определение запаса устойчивости по амплитуде

Запас устойчивости по амплитуде – величина, показывающая: во сколько раз необходимо изменить, то есть увеличить или уменьшить коэффициент передачи устойчивой системы, чтобы перевести эту систему на границу устойчивости. Запас устойчивости по амплитуде для устойчивой системы должен быть больше единицы. Кроме того, он может измеряться в децибелах и для устойчивой системы может принимать только положительные значения.

Для абсолютно устойчивой системы запас устойчивости по амплитуде может быть найден по соотношению . Так если для примера 6.4 задать значение k =3, запас устойчивости составит или в децибелах L_{a 1} = 20 lgU ₁=20 lg 5=14 дБ

Таким образом, если для данной системы k =3, остается возможность в случае необходимости увеличить его значение, но не более чем в 5 раз.

Для условно устойчивой системы при определении запаса устойчивости по амплитуде следует использовать соотношение .

Примем для примера 6.5 T ₁ = 1; T ₂=0,2; k =20. Тогда полученные выше условия будут выполнены, а критическое значение коэффициента передачи составит . Запас устойчивости по амплитуде или L_{a 2} = 20 lgU ₂=20 lg 24≈28 дБ.

Таким образом, можно допустить для данной системы снижение величины коэффициента передачи, но не более чем в 24 раза.

Параметрический синтез системы

Параметрическим синтезом называют выбор значений параметров управляющего или корректирующего устройства, обеспечивающих требуемое качество системы, при заданной структуре системы.

Пример 6.6. Найти значение коэффициента гибкой обратной связи , обеспечивающее запас устойчивости по амплитуде 20 дБ для системы, показанной на рис. 56, с параметрами: k= 10; k ₁ = 1; T= 0,4.

Рис.56.

Для правильного понимания смысла задачи, прежде всего, отметим, что понятие запаса устойчивости по амплитуде связано исключительно со значением коэффициента передачи разомкнутой системы k. Таким образом, требуется найти такое значение коэффициента k ₂, чтобы значение k отличалось от критического на 20 дБ, то есть в 10 раз.

Сначала необходимо выяснить характер ограничения на величину k. Для этого составим характеристический полином и получим условие устойчивости:

,

D (s) =T ² s ³ + 2 Ts ² + (kk ₂ + 1) s+kk ₁,

,

или

В зависимости от знака сомножителя при k при решении полученного неравенства необходимо рассмотреть два варианта:

- при , то есть , получим , что выполняется при любых положительных значениях k, то есть критическое значение коэффициента передачи в этом случае отсутствует и определить запас устойчивости невозможно;

- при получим или .

Для обеспечения требуемого запаса устойчивости должно соблюдаться соотношение , то есть должно быть k _кр=100.

Для получения окончательного результата составим уравнение:

.

Ответ: k ₂=0,19.

 

Контрольные вопросы и задачи для самостоятельной работы

1. Проанализируйте устойчивость систем с известными характеристическими полиномами, используя, в случае необходимости, помимо необходимого условия устойчивости, критерий Гурвица (варианты ответов: система устойчива, неустойчива, на границе устойчивости с указанием типа границы):

а) ; б) ;

в) ; г) ;

д) ; е) .

2. Для системы со структурно-динамической схемой на рис. 57:

а) получите условие устойчивости, определить характер устойчивости;

б) найдите критическое значение коэффициента передачи при k ₁=0,5; k ₃=10; T= 0,1;

в) найдите значение k ₁, обеспечивающее запас устойчивости по амплитуде 12 дБ при k ₂=5; k ₃=10; T= 0,1.

Рис.57.

Практическое занятие 7

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: