 |
Анализ устойчивости линейных стационарных систем
|
|
|
|
(частотные методы)
Наиболее широкие возможности анализа и синтеза систем предоставляют частотные критерии устойчивости Михайлова и Найквиста.
Критерий Михайлова предусматривает работу с характеристическим полиномом замкнутой системы
D (s) =a 0 sn+a 1 sn- 1 +…+an.
После подстановки 
получим так называемый характеристический комплекс:
,
где
,
,
,
-
соответственно вещественная и мнимая части, модуль и аргумент характеристического комплекса.
Характеристический комплекс также принято отображать на комплексной плоскости в виде годографа – кривой Михайлова.
Для устойчивой системы кривая Михайлова начинается на положительной горизонтальной полуоси (при 
D (0)= an), имеет плавную спиралевидную форму (расходящаяся спираль), проходит последовательно n квадрантов в направлении против часовой стрелки и уходит в бесконечность в n- ом квадранте, как показано на рис. 58.
Рис.58.
Для системы, находящейся на апериодической границе устойчивости (an =0), кривая Михайлова выходит из начала координат (рис. 59а).
Рис.59.
Для системы, находящейся на колебательной границе устойчивости, на частоте незатухающих колебаний в системе кривая Михайлова пройдет через начало координат (рис. 59б):
,
то есть одновременно имеет место
и 
.
Примеры кривых Михайлова для неустойчивых систем приведены на рис. 60.
Рис.60.
Для использования данного критерия можно обойтись без построения кривой Михайлова. Пронумеруем последовательно частоты, соответствующие точкам пересечения кривой Михайлова с осями координат (рис. 61).
Рис.61.
Частоты, соответствующие точкам пересечения с вертикальной осью, получат нечетные номера, с горизонтальной – четные:
, 
.
|
|
|
В результате критерий устойчивости Михайлова сводится к системе неравенств:
.
При 
получим апериодическую границу устойчивости, при 
–колебательную. Нарушение хотя бы одного неравенства будет признаком неустойчивости системы.
Пример 7.1. Получить условие устойчивости для системы со структурной схемой на рис. 54.
Составим характеристический полином
D (s) =T 1 T 2 s 3 + (T 1 +T 2) s 2 +s+k
и характеристический комплекс
.
Выделим его вещественную и мнимую части и составим уравнения:
.
.
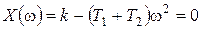Найдем их положительные решения
, 
и составим неравенства в соответствии с критерием Михайлова:
: 
.
Решив последнее неравенство относительно коэффициента передачи, получим условие устойчивости:
.
Критерий устойчивости Найквиста предусматривает анализ устойчивости замкнутой системы по частотным характеристикам разомкнутой системы: 
и 
или АФХ разомкнутой системы, или 
и 
.
Основная формулировка критерия устойчивости Найквиста относится к системе с единичной отрицательной обратной связью, когда знаменатель передаточной функции разомкнутой системы не имеет нулевых и мнимых корней: для устойчивости замкнутой системы необходимо и достаточно, чтобы при изменении частоты от - 
до угол поворота изображающего вектора ЧПФ разомкнутой системы 
относительно точки с координатами (-1; 0 j) составил 
, где l - количество корней знаменателя передаточной функции разомкнутой системы, лежащих в правой полуплоскости.
Иногда говорят: АФХ разомкнутой системы должна охватить точку с координатами (-1; 0 j) l раз в положительном направлении.
При l =0 АФХ разомкнутой системы не должна охватывать эту точку.
Пример 7.2. Проанализировать устойчивость замкнутой системы с единичной отрицательной обратной связью при 
, k =10, T 1=3 c., T 2=0,5 c., T 3=0,2 c.
Получим частотные характеристики разомкнутой системы:
,
.
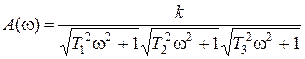Полученное выражение однозначно определяет вид АЧХ (рис. 62).
Рис.62.
|
|
|
Для однозначного определения вида ФЧХ установим ее наклон в окрестности :
.
Следовательно, за счет большой величины T 1 на малых частотах ФЧХ изменяется в положительном направлении. График ФЧХ показан на рис. 63а, приближенная АФХ – на рис. 63б.
Рис.63.
Для рассматриваемой системы l= 1, следовательно, для устойчивости замкнутой системы АФХ должна описать вокруг точки (-1; 0 j) дугу длиной 
в положительном направлении, что и будет иметь место в случае, показанном на рис. 63б. Это, очевидно, будет иметь место, если точка пересечения АФХ с горизонтальной осью на частоте 
будет ближе к началу координат, чем точка (-1; 0 j).
Для проверки устойчивости найдем , для чего получим МЧХ разомкнутой системы и приравняем к нулю:
,
,
: 
с-1.
Теперь найдем расстояние от точки пересечения АФХ с горизонтальной осью до начала координат:
.
Следовательно, система устойчива. Запас устойчивости по амплитуде нетрудно найти из геометрических соображений: 
.
Пример 7.3. Проанализировать устойчивость замкнутой системы с единичной отрицательной обратной связью и асимптотической ЛАХ разомкнутой системы на рис. 64. Принять, что система минимально-фазовая (передаточная функция разомкнутой системы не содержит нулей (корней числителя) и полюсов (корней знаменателя) в правой полуплоскости).
Рис.64.
По числовым данным на рис. 64 с учетом материалов практического занятия 4 (пример 4.9) и условия минимально-фазовости определяем наклоны участков асимптотической ЛАХ: -60; -40; -20 дБ /дек – и восстанавливаем передаточную функцию разомкнутой системы:
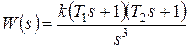. (7.1)
По сопрягающим частотам находим значения постоянных времени T 1=1,25; T 2=0,5.
Теперь находим опорную точку первого участка асимптотической ЛАХ и определяем коэффициент передачи разомкнутой системы: L ас(2)=8дБ; L ас(0,8)=24дБ. Координаты опорной точки: 
, L (1)(1)=18дБ. Из уравнения 20lg k= 18 найдем k =8.
Далее решение задачи может быть продолжено разными способами. Рассмотрим основные из них.
Решим задачу с помощью критерия Гурвица. Составим характеристический полином и второй определитель Гурвица:
D (s) = s 3 +kT 1 T 2 s 2 +k (T 1 +T 2) s+k,
.
Подстановка в определитель количественных данных задачи позволяет сделать вывод об устойчивости системы.
.
Теперь найдем условие устойчивости:
|
|
|
,
,
из которого следует, что система условно устойчива.
Найдем критический коэффициент передачи
,
и запас устойчивости по амплитуде:
, 
.
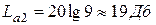Теперь решим задачу с помощью критерия Найквиста, следствием которого является простое правило проверки устойчивости по знаку величины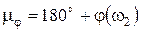 
, где 
– частота среза, определяемая по АЧХ разомкнутой системы по условию 
или по ЛАХ по условию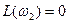 
. Если 
, то замкнутая система устойчива, а величина 
является запасом устойчивости по фазе.
Составим выражение для ФЧХ:
.
Частота среза в соответствии с рис. 64 составляет 
. Выполним расчеты:
,
.
Вывод: замкнутая система устойчива, запас устойчивости по фазе 
.
Отметим, что корректность использования для расчетов асимптотической ЛАХ определяется удаленностью расчетной частоты от ближайшей сопрягающей. В нашем случае расстояние между использованной при расчетах частотой среза 
и сопрягающей частотой 
составляет 0,4 декады, что с учетом оценок, представленных на с. 35, считается допустимым.
Полностью логарифмические характеристики рассматриваемой разомкнутой системы представлены на рис. 65.
Рис.65.
Пример 7.4. Проанализировать устойчивость замкнутой системы с единичной отрицательной обратной связью при 
, k =10, T 1=0,1 c., T 2=1 c., T 3=2 c.
Получим частотные характеристики системы:
, (7.1)
. (7.2)
Анализ (7.1) показывает, что расстояние от начала координат до точек АФХ 
при 
и 
(АФХ уходит в бесконечность вдоль асимптоты), а при 
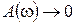, то есть АФХ приходит в начало координат.
В соответствии с (7.2) угол наклона вектора, направленного из начала координат в точки АФХ, имеет предельные значения в положительном диапазоне частот 
, 
, монотонно изменяется в положительном направлении во всем диапазоне, за исключением частоты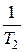 
, при переходе через которую он получает скачкообразное приращение величиной 
.
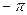Найдем для определенности значение ФЧХ, достигаемое при 
и определяющее наклон асимптоты:
.
Отметим с учетом выводов предыдущего абзаца, что при 
асимптота будет иметь угол наклона –201°, то есть отобразится симметрично началу координат.
|
|
|
АФХ разомкнутой системы для 
представлена на рис. 66.
Рис. 66.
Для анализа устойчивости с помощью критерия Найквиста при наличии в знаменателе передаточной функции разомкнутой системы нулевых и чисто мнимых корней АФХ разомкнутой системы дополняется дугами бесконечно большого радиуса в направлении по часовой стрелке на всех частотах, соответствующих таким корням. Длина каждой дуги 
, где r – кратность корня.
При использовании для анализа устойчивости ветви АФХ, соответствующей положительным частотам, она дополняется в окрестности положительной вещественной полуосью и дугой бесконечно большого радиуса длиной 
. Соответствующие дуги на рис. 66 показаны пунктиром.
АФХ позволяет сделать вывод о том, что замкнутая система будет устойчива, если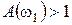 
. Проверим это:
,
,
,
.
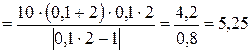Итак, замкнутая система условно устойчива, причем 
дает величину запаса устойчивости по амплитуде U 2=5,25 в абсолютных единицах или 
.
Контрольные вопросы и задачи для самостоятельной работы
1. Проанализируйте устойчивость систем из примеров 7.2-7.4 с помощью критерия Михайлова:
а) проверьте устойчивость при заданных числовых значениях параметров;
б) получите условие устойчивости в общем виде.
2. Постройте в общем виде АФХ и логарифмические частотные характеристики разомкнутой системы из примера 7.1. Получите условие устойчивости с помощью критерия Найквиста:
а) путем анализа АФХ;
б) путем анализа логарифмических частотных характеристик.
3. На рис. 65 пунктирной линией показано дополнение ЛФЧХ, соответствующее дополнению АФХ данной системы дугой бесконечно большого радиуса для анализа устойчивости по критерию Найквиста. Постройте логарифмические частотные характеристики для систем из примеров 7.1, 7.3-7.4 и выполните аналогичные дополнения.
4. Проанализируйте устойчивость систем из примеров 7.1-7.4 путем подсчета переходов [1]:
а) АФХ через отрезок горизонтальной оси левее точки (-1; 0 j);
б) ЛФЧХ через критические отрезки оси частот, определяемые по условию 
.
5. С учетом условия минимально-фазовости для замкнутой системы с асимптотической ЛАХ в разомкнутом состоянии, показанной на рис. 67:
а) получите условия устойчивости;
б) определите, при каком соотношении параметров система будет иметь запас устойчивости 26 дБ.
Рис.67.
Рис.68
6. Проанализировать устойчивость замкнутой системы с единичной отрицательной обратной связью и асимптотической ЛАХ разомкнутой системы на рис. 68. Принять, что система минимально-фазовая.
Практическое занятие 8
|
|
|
