 |
Примеры синтеза систем управления
|
|
|
|
В рамках данного практического занятия рассматриваются некоторые частные задачи параметрического синтеза – выбора значений параметров систем при заданных структурах из условий обеспечения требуемых значений показателей качества.
Пример 9.1.
Известен характеристический полином замкнутой системы с единичной обратной связью:
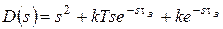, T =10 c.
1. Подобрать значение k, обеспечивающее x уст.=0,1 при задающем воздействии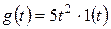 
.
2. При каком предельном значении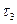 
при найденном k запас устойчивости по фазе будет не менее 30°?
При решении этой задачи учтем математическое описание особого динамического звена – звена с запаздыванием, или элемента запаздывания, обеспечивающего смещение входного сигнала во времени на величину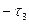 
. Передаточная функция элемента запаздывания получается непосредственно на основе теоремы запаздывания для преобразования Лапласа:
.
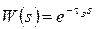Переходная характеристика такого звена имеет вид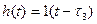 
.
Получим его частотные характеристики:
,
,
.
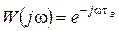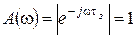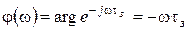Следовательно, данное звено не изменяет амплитуду входного сигнала, но вносит отрицательный фазовый сдвиг, неограниченно возрастающий с увеличением частоты. Отметим также, что наличие в системе такого звена не влияет и на установившуюся ошибку, так как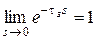 
.
По заданному характеристическому полиному можно сделать вывод о наличии в системе звена с запаздыванием и восстановить передаточную функцию разомкнутой системы:
.
Найдем передаточную функцию замкнутой системы по ошибке:
.
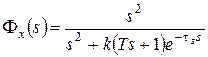Рассчитаем установившуюся ошибку и приравняем ее к допустимому значению:
,
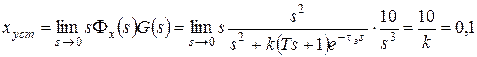откуда k= 100.
Запишем выражения для АЧХ и ФЧХ
,
.
и построим логарифмические характеристики разомкнутой системы (рис. 76).
|
|
|
Рис. 76.
По асимптотической ЛАХ найдем частоту среза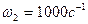 
.
Теперь составим выражение для определения запаса устойчивости по фазе:
,
и с учетом его допустимого значения получим уравнение для определения искомого значения :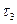
,
откуда
,
,
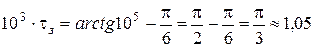с.
Пример 9.2.
Подобрать коэффициенты ПД-регулятора, обеспечивающие колебательность и установившуюся ошибку не более 0,01 при задающем воздействии 
для объекта управления с заданной моделью:
,
,
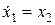y=x 1,
при следующих исходных данных: T= 0,1; k 3=10; g 0=10; v= 2;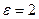 
.
ПД (пропорционально-дифференциальный) регулятор реализует закон управления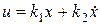 
, где x=g-y.
Составим структурно-динамическую схему системы (рис. 77) и получим передаточные функции:
Рис.77.
,
.
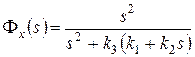Найдем установившуюся ошибку и учтем ее допустимое значение:
,
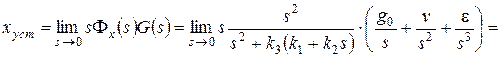
откуда k 1³20. Для последующих расчетов примем k 1=20.
Найдем корни характеристического полинома:
,
.
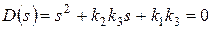Возможность обеспечить требуемую колебательность будет иметь место в том случае, если корни будут комплексными, то есть при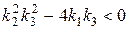 
. Решим это неравенство относительно искомого коэффициента k 2:
,
.
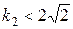При выполнении этого условия получим:
, 
, 
.
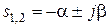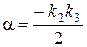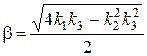Составим и решим уравнение
,
,
,
.
.
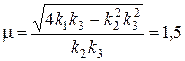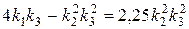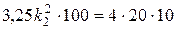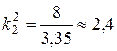Искомое значение второго коэффициента ПД-регулятора k 2≈1,6.
Пример 9.3.
Подобрать k y и k ос, обеспечивающие астатизм первого порядка по задающему воздействию и запас устойчивости по амплитуде 8 дБ для системы со структурно-динамической схемой на рис. 78. Принять k 0=2; Т 1=0,2; T 2=0,1.
Рис. 78.
Условия задачи предусматривают обеспечение астатизма первого порядка для статической системы путем введения неединичной обратной связи.
Составим передаточную функцию замкнутой системы по ошибке:
,
,
.
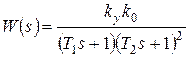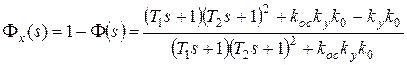Найдем выражение для расчета установившейся ошибки и получим соотношение для выбора коэффициента k ос из условия xуст =0 при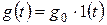 
:
,
,
.
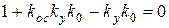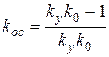Рассмотрим характеристический полином замкнутой системы:
|
|
|
.
Необходимое условие устойчивости выполняется при любых значениях параметров, критерий устойчивости Гурвица приводит к неравенству:
,
или для коэффициента передачи разомкнутой системы k = kуk 0:
.
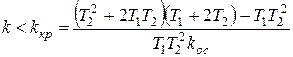Требуемый запас устойчивости по амплитуде 8 дБ в соответствии с соотношением 20 lgU 1=8 дБ составит в абсолютных единицах U 1=2,5, что приводит к следующему соотношению:
.
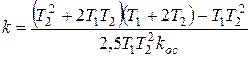С учетом числовых данных задачи получаем систему уравнений для определения двух искомых коэффициентов:
,
.
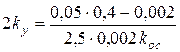Ее решение позволяет получить следующие результаты:
,
,
,
, 
.
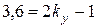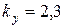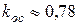Контрольные вопросы и задачи для самостоятельной работы
1. Проанализируйте влияние величины каждого параметра систем из примеров 9.2, 9.3 на запас устойчивости системы.
2. Для системы на рис. 79 подберите значения коэффициентов k в и k ос, обеспечивающие равенство нулю установившейся ошибки пр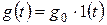и и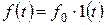 
.
Рис.79.
3. Проанализируйте влияние величин подбираемых в предыдущей задаче коэффициентов на запас устойчивости системы.
4. Среди типовых динамических звеньев выбрать регулятор для системы на рис. 80 и подобрать его параметры, обеспечивающие получение установившейся ошибки x уст=0,1 при запасе устойчивости 14 дБ при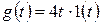 
; k 0=2; Т 1=0,02; T 2=0,1.
Рис.80.
5. Для исходной структуры (без связи, показанной пунктиром) оценить точность и запас устойчивости системы на рис. 81 при 
, k 1=4; k 2=5; Т =0,01.
Подобрать значение k в, обеспечивающее повышение точности в 3 раза. Как изменится запас устойчивости?
Рис.81.
Домашнее задание № 1
|
|
|
