 |
Преобразование структурных схем. Передаточные функции
|
|
|
|
Замкнутых систем
Вспомним основные правила, которым подчиняется работа со структурными схемами систем.
Получение передаточных функций для участков с типовым соединением звеньев
1. Последовательное соединение (рис.37):
.
Рис. 37.
2. Параллельное соединение (рис. 38а):
Рис. 38.
.
Отметим, что в общем случае при параллельном соединении сумма передаточных функций является алгебраической. Так для цепи на рис. 38б имеет место:
.
3. Отрицательная обратная связь (рис. 39а):
Рис. 39.
. (5.1)
4. Положительная обратная связь (рис. 39б):
.
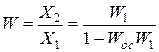Рассмотренные типовые варианты не исчерпывают всего многообразия вариантов соединения звеньев на структурных схемах систем. Поэтому для решения практических задач часто требуется преобразование структурных схем, например, перенос сумматора или точки поступления сигнала через звено, перенос точки разветвления сигналов и др.
Рассмотрим фрагмент структурной схемы, показанный на рис. 40а. К нему невозможно прямо применить ни одно из рассмотренных правил.
Для того, чтобы привести данную структуру к сочетанию участков типового соединения звеньев, необходимо ее преобразовать, например, поменять местами точку разветвления А и звено с передаточной функцией W 2 (рис. 40б). Такие преобразования возможны, если будет обеспечена эквивалентность выходных сигналов исходного и преобразованного участка схемы.
Рис. 40.
В исходной схеме (рис. 40а) сигнал x 2 поступает из точки А в точку В без изменений. После переноса точки разветвления через звено (рис. 40б), он будет подвергаться преобразованию, описанному передаточной функцией W 2. Следовательно, необходимо дополнить структурную схему звеном, выполняющим обратное преобразование. Приведенным рассуждениям соответствует равенство, подтверждающее требуемую эквивалентность: 
.
|
|
|
Передаточные функции систем управления
В системах управления могут присутствовать несколько входных сигналов: одно или несколько задающих воздействий g, одно или несколько возмущающих воздействий f, причем разные входные сигналы могут поступать в различные точки системы.
В системе могут рассматриваться один или несколько выходных сигналов, также измеряемых в различных точках системы.
Даже если выходной сигнал y единственный, с целью анализа точности системы, наравне с ним рассматривается сигнал ошибки: 
.
Таким образом, при описании замкнутой системы всегда приходится рассматривать несколько передаточных функций.
Сформулированное выше для динамических звеньев определение передаточной функции распространяется и на систему управления в целом, но в замкнутой системе существуют определённые правила выделения передаточных функций.
Виды передаточных функций, рассматриваемых для замкнутой системы, перечислим на основе структуры, представленной на рис. 41.
Рис. 41.
Для задающего воздействия рассматривается следующий набор передаточных функций.
Передаточная функция разомкнутой системы – отношение изображений выходного сигнала и задающего воздействия без учета главной обратной связи:
.
Для примера на рисунке получим: 
.
Любая передаточная функция в общем случае представляет собой отношение полиномов от аргумента s. Для передаточной функции разомкнутой системы используются следующие условные обозначения этих полиномов:
. (5.2)
Основная передаточная функция замкнутой системы – отношение изображений выходного сигнала и задающего воздействия для системы в целом. С учетом (4.1) для структуры на рис. 41 получим:
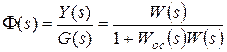. (5.3)
Передаточная функция замкнутой системы по ошибке – отношение изображений сигнала ошибки и задающего воздействия:
|
|
|
.
Отметим, что соотношение
получено только на основе определений передаточных функций и сигнала ошибки и справедливо для систем любой структуры.
Для системы с единичной отрицательной обратной связью получение передаточных функций значительно упрощается.
При 
для основной передаточной функции получаем
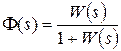
или через полиномы (4.2);
. (5.4)
Для передаточной функции по ошибке:
,
или через полиномы:
. (5.5)
Для возмущающего воздействия рассматривается аналогичный набор передаточных функций.
Передаточная функция разомкнутой системы по возмущению – отношение изображений выходного сигнала и возмущающего воздействия без учета главной обратной связи:
.
На практике эта передаточная функция определяется как передаточная функция участка прямой цепи системы от точки приложения возмущающего воздействия до выхода системы. Для рассматриваемого примера получим: 
.
Рис. 42.
Передаточная функция замкнутой системы по возмущению – отношение изображений выходного сигнала и возмущающего воздействия для системы в целом. При ее определении необходимо учитывать, что участок прямой цепи от входа системы до точки приложения возмущающего воздействия войдет для него в состав обратной связи (рис. 42).
В результате получим:
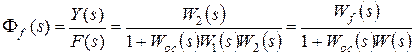. (5.6)
При : 
.
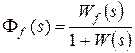Передаточная функция замкнутой системы по ошибке от возмущающего воздействия – отношение изображений сигнала ошибки и возмущающего воздействия:
, (5.7)
так как при определении передаточной функции по возмущению задающее воздействие должно быть принято равным нулю. Данное соотношение также является универсальным.
Пример 5.1. Получить основную передаточную функцию замкнутой системы (рис. 43) и записать соответствующее уравнение.
Рис. 43.
Основная передаточная функция определяется по соотношению (5.3). Для ее получения учтем следующие особенности примера:
1. Главная обратная связь – единичная отрицательная. Следовательно, можно использовать соотношение (5.4).
2. При определении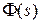 
возмущение f следует исключить.
Теперь рассматриваем участки структурной схемы, соответствующие вариантам типового соединения звеньев, и укрупняем их (рис. 44).
Рис. 44.
Передаточная функция W 1 соответствует участку с положительной обратной связью:
|
|
|
.
Передаточная функция W 2 соответствует участку с отрицательной обратной связью:
.
Передаточная функция W 3 соответствует участку с параллельным соединением звеньев:
.
Укрупним (рис. 45) последний участок (отрицательная обратная связь):
.
Рис. 45.
Теперь получим передаточную функцию разомкнутой системы:
.
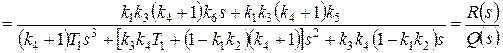Искомая основная передаточная функция в соответствии с (5.4):
.
Для сокращения записи введем обозначения:
,
,
,
,
,
,
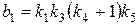и запишем дифференциальное уравнение, связывающее соответствующие этой передаточной функции входной g (t) и выходной y (t) сигналы:
.
Пример 5.2. Для рассмотренной в предыдущем примере структурно-динамической схемы получить передаточную функцию замкнутой системы по ошибке и записать соответствующее уравнение.
С учетом единичной отрицательной обратной связи следует воспользоваться (5.5) и полиномами R и Q, полученными в примере 5.1:
.
Используя полученные выше обозначения для коэффициентов знаменателя и введя новые для коэффициентов числителя:
,
,
,
запишем дифференциальное уравнение, связывающее соответствующие этой передаточной функции сигналы:
.
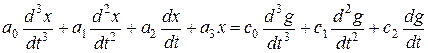Пример 5.3. Для рассмотренной в предыдущих примерах структурно-динамической схемы получить передаточную функцию замкнутой системы по возмущению и записать соответствующее уравнение.
С учетом полученных выше результатов можно рассматривать структурную схему, представленную на рис. 46а, которую приведем к виду на рис. 46б, где:
,
.
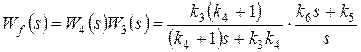Рис. 46.
Теперь воспользуемся соотношением (5.6):
.
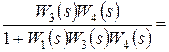
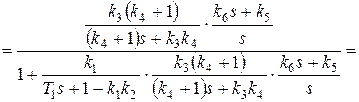
В дополнение к использованным выше введем обозначения:
,
,
,
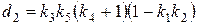и запишем дифференциальное уравнение, связывающее соответствующие этой передаточной функции входной f (t) и выходной y (t) сигналы:
.
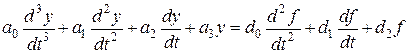Пример 5.4. Для рассмотренной в предыдущих примерах структурно-динамической схемы получить передаточную функцию замкнутой системы по ошибке от возмущающего воздействия и записать соответствующее уравнение.
С учетом (5.7) результаты решения этого примера отличаются от предыдущего только знаком:
|
|
|
,
.
Контрольные вопросы и задачи для самостоятельной работы
1. Сравните знаменатели передаточных функций замкнутых систем, полученные в материалах практического занятия №5 и сделайте общий вывод.
2. На рис. 47-48 под литерой «а» представлены исходные фрагменты структурно-динамических схем, под литерой «б» - преобразованные фрагменты. Подберите передаточные функции для дополнительных звеньев, показанных пунктиром, так, чтобы обеспечивалась эквивалентность преобразования.
Рис. 47.
Рис. 48.
3. Получите рассмотренный в примерах 5.1-5.4 набор передаточных функций для систем со структурными схемами на рис. 49-50.
Рис.49.
Рис. 50.
Практическое занятие 6
|
|
|
