 |
Составление математической модели и получение характеристик динамического звена
|
|
|
|
1. Составить дифференциальное уравнение и передаточную функцию динамического звена для заданной схемы четырехполюсника (таблица 2).
2. Получить аналитическое выражение и построить переходную характеристику h (t)= U вых(t) при U вх(t) = 1(t) и нулевых начальных условиях (для момента времени, который непосредственно предшествует моменту приложения воздействия, при учете, что процессы в цепи до этого момента времени отсутствуют).
3. Получить аналитические выражения и построить частотные характеристики:
– амплитудно-частотную характеристику 
,
– фазо-частотную характеристику 
,
– амплитудно-фазовую частотную характеристику,
– асимптотическую и точную ЛАХ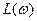 
и логарифмическую фазо-частотную характеристику .
4. Проанализировать динамические свойства звена с точки зрения быстроты затухания переходного процесса (найти время переходного процесса), формы кривой, склонности цепи к колебаниям (оценить период и собственную частоту колебаний, частоту среза, коэффициент демпфирования, степень затухания за период), оценить, как преобразует исследуемая цепь входной сигнал и какой вносит фазовый сдвиг.
Таблица 2 – Индивидуальные варианты заданий
| Схемы четырехполюсников | Числовые данные | |||||||||
Схема 1
| Параметры | Варианты | ||||||||
 , с
| 0,2 | 0,5 | 0,5 | 1,0 | 1,5 | 1,8 | 2,0 | 2,5 | 3,0 | 4,0 |
 , с
| 0,1 | 0,1 | 0,2 | 0,2 | 1,0 | 0,5 | 1,5 | 0,5 | 1,5 | 0,6 |
Схема 2
| Параметры | Варианты | ||||||||
 , с
| 0,5 | 1,0 | 0,5 | 1,3 | 1.5 | 2.0 | 1,5 | 2,5 | 3,0 | 3,5 |
| , с
| 0,2 | 0,2 | 2.5 | 0,2 | 0,5 | 0,2 | 1,5 | 1,5 | 1,5 | 2,0 |
Схема 3
| Параметры | Варианты | ||||||||
 , с
| 0,5 | 0,5 | 1,0 | 1,5 | 1.5 | 3,0 | 3,5 | 2,0 | 3,0 | 3,0 |
 , с
| 1,5 | 2,0 | 2,0 | 2,5 | 0,5 | 5,0 | 5,5 | 3,0 | 1,5 | 2,0 |
Схема 4
| Параметры | Варианты | ||||||||
|
, с
| 0,5 | 0,4 | 1,0 | 0,5 | 1.5 | 2,0 | 1,2 | 2,0 | 3,0 | 3,0 |
| , с
| 1,5 | 2,0 | 2,0 | 2,5 | 0,5 | 5,0 | 5,0 | 3,0 | 1,5 | 2,0 |
Схема 5
| Параметры | Варианты | ||||||||
|
, с
| 1.5 | 0,2 | 1,0 | 0,5 | 1.5 | 2,0 | 1,0 | 2,0 | 3,0 | 3,0 |
| , с
| 0,5 | 1,0 | 2,0 | 3,0 | 2,5 | 4,0 | 5,0 | 3,0 | 1,5 | 2,0 |
|
|
|
Методические указания и требования к оформлению
1. При записи дифференциального уравнения и передаточной функции звена необходимо выполнять требования, приведенные в материалах практического занятия 1. В соответствии с получаемой формой модели ввести параметры динамического звена (коэффициент передачи, постоянные времени и др.) и выразить через параметры четырехполюсника.
Для схем 1-2 и 4-5 в случае, если полюса получаемой передаточной функции комплексные, ее знаменатель привести к виду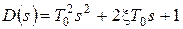 
, где 
– коэффициент демпфирования, при вещественных полюсах – к виду 
.
2. При построении графиков переходной и частотных характеристик звена с использованием средств автоматизации математических расчетов необходимо обеспечить оформление графиков в общепринятой форме.
При ручном построении графика необходимо рассчитывать 10-12 точек в содержательной части характеристики.
3. Для получения переходной характеристики допускается использовать классический (путем решения дифференциального уравнения) или операторный методы, рассмотренные в материалах практического занятия 2. Результаты представить в форме итогового выражения для h (t) и соответствующего графика.
При построении графика обеспечить отображение переходной характеристики на интервале времени, соответствующем 1,5 – 2 периодам колебаний, а при вещественных полюсах передаточной функции – в 1,5 – 2 раза превышающем время переходного процесса.
4. Для получения частотных характеристик использовать материалы практического занятия 3.
|
|
|
При построении АФХ использование разных масштабов по осям не допускается.
5. Для построения логарифмических частотных характеристик использовать систему координат, представленную на рис. 26, и материалы практического занятия 4.
6. При выполнении п.3 необходимо найти числовые значения всех указанных параметров, используя материалы практического занятия 8 и учебник [1], и сформулировать выводы о динамических свойствах звена, отображаемых полученными характеристиками.
При определении времени переходного процесса использовать два способа:
- с использованием степени устойчивости, определяемой по полюсам передаточной функции;
- непосредственно по графику переходной характеристики как момент времени, начиная с которого выполняется неравенство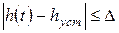 
, где 
, 
.
Домашнее задание № 2
|
|
|
