 |
Определение фазо-частотных характеристик
|
|
|
|
Пакетный файл ФЧХ.bat, исполняемый файл tau111hz.exe.
Сведения из теории
Основные сведения из теории представлены в материалах практического занятия № 3.
В процессе выполнения работы в случае регистрации ошибки при ответе на вопрос пользователю становятся доступны краткий обзор сведений из теории, соответствующий порядку решения задачи, а также демонстрация правильного решения задачи с необходимыми комментариями.
Порядок выполнения работы
1. После запуска пакетного файла ознакомьтесь с информацией на заставке программы и снимите ее нажатием любой клавиши (рис. 88).
Рис.88.
2. Внимательно изучите справочную информацию и инструкции на экране (рис. 89). Следуйте инструкциям о порядке использования клавиш в процессе выполнения работы.
Рис.89.
3. По заданной передаточной функции необходимо подобрать соответствующее выражение для фазо-частотной характеристики (рис. 89) Выбор производится из множества вариантов фазо-частотных характеристик, отсортированных по определенным признакам (количество постоянных времени, наличие колебательного звена или его отсутствие и др.).
4. Условием успешного выполнения работы является правильный подбор десяти характеристик подряд. Информация о количестве правильных ответов размещается в нижней части экрана. В случае ошибки при подборе очередной характеристик счетчик оставшихся до зачета вопросов устанавливается в исходное значение 10, и выполнение работы должно быть продолжено.
При ошибочном ответе программа указывает правильный вариант и пользователю предоставляется возможность получить краткую справку из теории (клавиша F1) и ознакомиться с разбором правильного ответа (клавиша F2).
|
|
|
Контрольные вопросы
1. Как связано предельное значение фазо-частотной характеристики при 
со степенями числителя и знаменателя передаточной функции для минимально-фазовых звеньев и систем?
2. Как связано предельное значение фазо-частотной характеристики при 
со степенями числителя и знаменателя передаточной функции для минимально-фазовых звеньев и систем?
Лабораторная работа № 3
Построение асимптотических логарифмических амплитудных
Характеристик
Работа предлагается в двух версиях: стандартной и упрощенной. В упрощенной версии не требуется проводить анализ резонансных свойств колебательных звеньев.
Стандартная версия – пакетный файл ЛАХ.bat, исполняемый файл tau140cr.exe.
Упрощенная версия – пакетный файл ЛАХУпр.bat, исполняемый файл tau140cz.exe.
Выбор версии для выполнения производится по указанию преподавателя.
Сведения из теории
В материалах практического занятия № 4 рассмотрены примеры построения логарифмических характеристик некоторых типовых звеньев, позволяющие обнаружить основные закономерности формирования асимптотических ЛАХ. Подробно с примерами рассмотрена процедура построения асимптотической ЛАХ разомкнутой системы, которую следует использовать при выполнении данной лабораторной работы.
Здесь подробнее рассмотрим особенности построения асимптотической ЛАХ колебательного звена.
Колебательное звено описывается тем же дифференциальным уравнением, что и апериодическое звено второго порядка
,
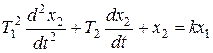однако корни характеристического уравнения должны быть комплексными, что будет выполняться при условии 
.
Передаточную функцию колебательного звена удобнее записать как 
, где коэффициент демпфирования 
, T=T 1, 
.
Отсюда:
,
,
,
Сопрягающая частота находится из условия равенства двух слагаемых под корнем – содержащих низшую и высшую степень частоты:
|
|
|
, 
.
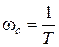На низких частотах, w<<1/ T, всеми слагаемыми, содержащими произведение w T, можно пренебречь по сравнению с единицей (w T <<1). В результате выражение для ЛАХ приближенно примет вид:
.
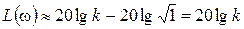Это уравнение горизонтальной прямой – асимптоты точной ЛАХ при w®0.
На высоких частотах, w>>1/ T, под корнем можно пренебречь всеми слагаемыми, кроме содержащего высшую степень частоты. Выражение для ЛАХ приближенно примет вид:
.
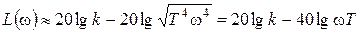Это выражение для прямой с наклоном –40дБ/дек, причем при w T =1, то есть на сопрягающей частоте она проходит через точку с вертикальной координатой 20lg k. Эта прямая является асимптотой точной ЛАХ при w®¥. Асимптоты ЛАХ пересекаются на сопрягающей частоте (рис. 90).
Рассмотрим формирование погрешности асимптотической ЛАХ для колебательного звена. Прежде всего, оценим величину этой погрешности на сопрягающей частоте. Для асимптотической ЛАХ получим:
.
Для точной ЛАХ:
.
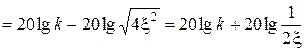Рис.90.
Величина погрешности 
зависит от величины x и изменяется от –6 дБ при x®1 до сколь угодно больших положительных значений при x®0.
Этот эффект обусловлен резонансными свойствами колебательного звена и в общем случае не позволяет при его анализе ограничиваться использованием только асимптотической ЛАХ.
Точные ЛАХ колебательного звена для различных значений x показаны на рисунке 90. По ним видно, что резонансная частота, доставляющая максимум ЛАХ, отличается от сопрягающей. Резонансная частота wр может быть найдена из условия:
.
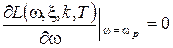Рекомендации по использованию асимптотической ЛАХ сводятся к следующему:
- при больших значениях x, когда резонансный пик отсутствует или не превышает величины 3дБ, допустимо использование асимптотической ЛАХ;
- при малых x, когда высота резонансного пика превышает 3дБ, должна использоваться точная ЛАХ.
Перед выполнением данной лабораторной работы в стандартной версии необходимо решить задачу № 6 из списка контрольных вопросов и задач для самостоятельной работы к практическому занятию № 4.
Порядок выполнения работы
1. После запуска пакетного файла ознакомьтесь с информацией на заставке программы и снимите ее нажатием любой клавиши.
2. Внимательно изучите справочную информацию и инструкции на экране (рис. 91, 92). Следуйте инструкциям о порядке использования клавиш в процессе выполнения работы.
|
|
|
Рис.91.
Рис.92.
3. Содержание каждой задачи состоит в построении асимптотической логарифмической амплитудной характеристики для заданной передаточной функции. Для этого требуется последовательно указать:
1) количество сопрягающих частот (рис. 93);
Рис.93.
2) значения сопрягающих частот в порядке возрастания (рис. 94);
Рис.94.
3) наклоны ЛАХ на участках последовательно слева направо (рис. 95);
Рис.95.
4) определить требуется ли учет резонанса (при наличии в системе колебательного звена если величина резонансного пика превышает 3дБ, должна использоваться точная ЛАХ, а не асимптотическая)
(примечание: в упрощенном варианте учет резонанса требуется для любого колебательного звена) (рис. 96);
Рис.96.
5) величину сопрягающей частоты, в окрестности которой наблюдается явление резонанса (данный вопрос формируется в случае, если при ответе на предыдущий пользователь указал необходимость учета резонанса) (рис. 97);
Рис.97.
6) координаты опорной точки для первого участка ЛАХ (рис. 98).
Рис.98.
4. Условием успешного выполнения работы является правильное решение пяти задач (рис. 99). Если при решении очередной задачи допущены ошибки, то после ответа на все вопросы в нижней части экрана появляется перечень ошибок. В этом случае требуется решить задачу заново, исправив указанные ошибки. При этом в зачет эта задача не идет (добавляется еще одна задача).
Рис.99.
Контрольные вопросы
1. Каким образом определяется ЛАХ звена или системы?
2. Чем отличается ЛАХ от АЧХ?
3. Какие возможности дает использование ЛАХ?
4. Сформулируйте основные правила построения ЛАХ.
5. Что такое асимптотическая ЛАХ?
6. На какой частоте достигает максимума погрешность асимптотической ЛАХ по отношению к точной ЛАХ?
7. Чем отличается передаточная функция апериодического звена второго порядка от передаточной функции колебательного звена?
8. Укажите значение коэффициента демпфирования при котором величина резонансного пика равна 3 дБ.
|
|
|
9. Как определить опорную точку при построении асимптотической логарифмической амплитудной характеристики?
10. Для построенной в процессе выполнения работы асимптотической ЛАХ оцените ее погрешности по отношению к точной на сопрягающих частотах и в их окрестности.
Лабораторная работа № 4
|
|
|
