 |
Оценка устойчивости по логарифмическим характеристикам
|
|
|
|
Пакетный файл Устойчивость.bat, исполняемый файл tau160cz.exe.
Сведения из теории
Содержание лабораторной работы включает в себя:
- проверку устойчивости системы по заданным ЛАХ и ЛФЧХ;
- определение характера устойчивости (абсолютная или условная);
- определение запасов устойчивости;
- поиск критического коэффициента усиления.
Оценка и анализ устойчивости систем в данной лабораторной работе основаны на использовании частотного критерия устойчивости Найквиста с применением логарифмических частотных характеристик разомкнутой системы. При этом вопрос об устойчивости рассматривается для замкнутой системы с единичной отрицательной обратной связью.
Правила построения ЛАХ и ЛФЧХ рассмотрены в материалах практического занятия №4. Основные сведения из теории устойчивости представлены в материалах практических занятий № 6-7. Подробное описание анализа устойчивости с помощью критерия Найквиста представлено в [1].
При работе с логарифмическими частотными характеристиками в общем случае наиболее удобно использовать форму критерия, основанную на подсчете переходов ЛФЧХ 
через горизонтальную ось на участках, где ЛАХ 
(критические участки). Положительным является переход в направлении увеличения значений , то есть сверху вниз, отрицательным – переход в обратном направлении.
Поскольку логарифмические частотные характеристики строятся для положительных частот, критерий устойчивости сводится к соблюдению равенства:
,
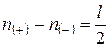где n (+) – количество «положительных» переходов, n (-) – количество «отрицательных» переходов, l - количество корней знаменателя передаточной функции разомкнутой системы, лежащих в правой полуплоскости (рис. 114).
|
|
|
Для частного случая l =0 (система устойчива или нейтрально устойчива в разомкнутом состоянии), который рассматривается в данной лабораторной работе, замкнутая система является устойчивой, если разность между количествами положительных и отрицательных переходов ЛФЧХ через критический участок горизонтальной оси равна нулю.
Рис.114.
Для систем, нейтрально устойчивых в разомкнутом состоянии (знаменатель передаточной функции содержит нулевые или мнимые корни), применение критерия Найквиста предусматривает необходимость дополнения ЛФЧХ вертикальными отрезками:
- для нулевого корня кратности r от уровня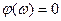 
до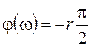 
на частоте ω→0;
- для мнимого корня также в отрицательном направлении (вверх) на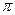 
, то есть в пределах разрыва ЛФЧХ на частоте, соответствующей этому корню.
При подсчете количества переходов дополняющие отрезки рассматриваются как составные части ЛФЧХ.
Рассмотрим пример анализа устойчивости системы с передаточной функцией
и логарифмическими частотными характеристиками на рис 115. Здесь l= 0, r= 3. ЛФЧХ должна быть дополнена при 
отрезком от 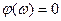до 
, показанном на рисунке пунктирной линией. Это дополнение обеспечивает отрицательный переход ЛФЧХ через горизонтальную ось, который для устойчивости замкнутой системы должен быть скомпенсирован положительным на критическом участке горизонтальной оси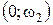 
. В результате приходим к условию устойчивости: 
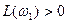, где частота 
определяется из условия 
.
Рис.115.
Представленные на рис. 115 логарифмические характеристики позволяют сделать вывод об устойчивости рассматриваемой системы.
По характеру устойчивости линейных систем различают абсолютно и условно устойчивые системы.
Устойчивую линейную систему, которая может утратить устойчивость за счет снижения коэффициента передачи, называют условно устойчивой. Все остальные устойчивые линейные системы называют абсолютно устойчивыми.
|
|
|
Изменение коэффициента передачи разомкнутой системы не влияет на ее ЛФЧХ, но приводит к плоско-параллельному смещению ее ЛАХ. При увеличении коэффициента передачи ЛАХ смещается вверх, при уменьшении – вниз.
Из рис. 115 видно, что уменьшение коэффициента передачи рассматриваемой системы приводит к уменьшению частоты среза 
. При совпадении точек пересечения ЛАХ и ЛФЧХ с горизонтальной осью (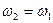
) будет достигнута граница устойчивости. Соответствующее значение коэффициента передачи называется критическим (k=k кр). При дальнейшем уменьшении коэффициента передачи точка положительного перехода (отметка частоты ) выйдет за пределы критического участка, и система потеряет устойчивость.
Таким образом, рассмотренная система является условно устойчивой.
Как следствие выполненных рассуждений отметим, что при l= 0 применение критерия Найквиста с использованием логарифмических частотных характеристик может быть сведено к сравнению значений двух частот, на которых характеристики пересекают горизонтальную ось: для ЛФЧХ (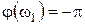
) и частоты среза для ЛАХ (L ()=0).
Если ЛФЧХ пересекает горизонтальную ось снизу вверх (в отрицательном направлении), для устойчивости замкнутой системы достаточно выполнения неравенства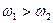 
(отрицательный переход за пределами критического отрезка). Это условие абсолютной устойчивости замкнутой системы.
Если ЛФЧХ пересекает горизонтальную ось сверху вниз (в положительном направлении), получаем условие условной устойчивости замкнутой системы: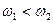 
.
При совпадении и получаем колебательную границу устойчивости.
Для устойчивых систем определяются показатели качества. В данной работе рассматриваются два из них – запасы устойчивости по амплитуде и по фазе.
Запас устойчивости по амплитуде – величина, показывающая: во сколько раз необходимо изменить, то есть увеличить или уменьшить коэффициент передачи устойчивой системы, чтобы перевести эту систему на границу устойчивости. Запас устойчивости по амплитуде для устойчивой системы должен быть больше единицы. Кроме того, он может измеряться в децибелах и для устойчивой системы может принимать только положительные значения.
Для абсолютно устойчивой системы запас устойчивости по амплитуде может быть найден по соотношению 
, где k – фактическое значение коэффициента передачи. Значение запаса устойчивости в децибелах La= 20 lgU 1 может быть найдено по логарифмическим характеристикам, как расстояние от ЛАХ до горизонтальной оси на частоте (рис. 116а).
|
|
|
Для условно устойчивой системы при определении запаса устойчивости по амплитуде следует использовать соотношение 
. Соответствующее значение в децибелах La= 20 lgU 2 определяется аналогично (рис. 116б).
Рис.116.
Запас устойчивости по фазе 
показывает, какой по абсолютной величине дополнительный отрицательный фазовый сдвиг нужно добавить к фазовому сдвигу, обеспечиваемому разомкнутой системой, чтобы перевести устойчивую замкнутую систему на границу устойчивости. Он может быть найден по соотношению: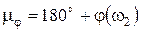 
и для устойчивой системы должен быть положительным, что, очевидно, будет иметь место в случаях, когда ЛФЧХ на частоте среза проходит ниже горизонтальной оси. В этих случаях графически запас устойчивости по фазе определяется как расстояние от ЛФЧХ до горизонтальной оси на частоте среза (рис. 116).
В качестве универсального способа проверки устойчивости можно использовать проверку знака выражения 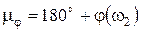. Для устойчивой системы 
. При 
система неустойчива; при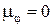 
имеет место граница устойчивости.
Для неустойчивой системы практический интерес представляет возможность обеспечения устойчивости. Если частоты, соответствующие точкам пересечения с горизонтальной осью ЛФЧХ и ЛАХ для рассматриваемой системы существуют, неустойчивую систему можно перевести на границу устойчивости (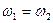
) путем уменьшения или увеличения коэффициента передачи (соответственно смещая ЛАХ вверх или вниз). Дальнейшее смещение ЛАХ обеспечит устойчивость такой системы.
Направление требуемого смещения ЛАХ нетрудно определить по графикам.
Если для достижения границы устойчивости ЛАХ необходимо поднять на расстояние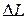 
, это будет соответствовать увеличению коэффициента передачи в 
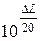раз, и критическое значение коэффициента передачи составит 
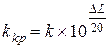, где его k - исходное значение, 
– расстояние от ЛАХ до горизонтальной оси на частоте .
|
|
|
Если для достижения границы устойчивости ЛАХ необходимо опустить на расстояние 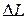, это будет соответствовать уменьшению коэффициента передачи в 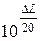раз, и критическое значение коэффициента передачи составит 
.
При решении задач анализа или синтеза системы управления с применением логарифмических частотных характеристик важное значение имеет возможность использования асимптотической ЛАХ, так как ее построение и расчеты на ее основе выполнять удобнее и проще по сравнению с точной характеристикой.
В материалах практического занятия № 4 приводится оценка погрешностей асимптотической ЛАХ, достигающих максимальных значений в окрестности сопрягающих частот. В ряде случаев эти погрешности могут существенно повлиять на результаты решаемых задач и являются недопустимыми.
Рассмотрим примеры таких ситуаций.
Для системы рассмотренной выше передаточной функцией и меньшим коэффициентом передачи логарифмические характеристики показаны на рис. 117. Здесь использование асимптотической ЛАХ приводит к выводу о неустойчивости системы. Ошибочность данного вывода становится ясна, если выполнить проверку устойчивости с использованием точной ЛАХ (показана пунктиром).
Рис.117.
Вернемся к рис. 115. Очевидно, как точная, так и асимптотическая ЛАХ позволят сделать однозначный вывод об устойчивости системы. Но поскольку для рассматриваемой системы частота совпадает с сопрягающей частотой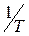 
, запас устойчивости по амплитуде, измеренный по асимптотической ЛАХ и реальной ЛАХ будет различаться на 6 дБ (в абсолютных единицах – в два раза).
На рис. 118 показаны логарифмические характеристики устойчивой системы. Запас устойчивости по фазе, измеренный на частоте среза точной ЛАХ , составляет 45°, а на частоте среза асимптотической ЛАХ получаем 38°.
Рис.118.
Перед выполнением данной лабораторной работы рекомендуется дополнительно ознакомиться с примером № 7.3 из практического занятия № 7 и решить задачи № 2-5 из списка контрольных вопросов и задач для самостоятельной работы к практическому занятию № 7.
Порядок выполнения работы
1. После запуска пакетного файла ознакомьтесь с информацией на заставке программы (рис. 119) и снимите ее нажатием любой клавиши.
Рис.119.
2. Внимательно изучите справочную информацию и инструкции на экране (рис. 120) и следуйте им в процессе выполнения работы.
Рис.120.
3. В процессе решения каждой задачи лабораторной работы требуется последовательно ответить на вопросы, перечень которых определяется свойствами рассматриваемой в задаче системы.
|
|
|
1) Допустимо ли в данной задаче использовать асимптотическую ЛАХ (рис. 121)?
Рис.121.
Использование асимптотической ЛАХ для анализа устойчивости системы допустимо при следующих условиях:
- выводы об устойчивости системы, получаемые с использованием точной и асимптотической ЛАХ, совпадают;
- расхождение между точной и асимптотической ЛАХ на частотах, соответствующих пересечению ЛФЧХ с горизонтальной осью, не превышает 2 дБ;
- разность значений ЛФЧХ для частот среза, определяемых по точной и асимптотической ЛАХ, не превышает 3°.
Если хотя бы одно из условий нарушено (рис. 121), использование асимптотической ЛАХ следует считать недопустимым.
Для получения точных значений используемых характеристик в лабораторной работе предусмотрен специальный инструмент – «линейка». Ее исходное расположение – в центре экрана. Клавишами «→», «←» обеспечивается перемещение линейки, клавишами «↑», «↓» можно изменять скорость перемещения.
В правом нижнем углу экрана расположено поле, в котором отображаются значение частоты, соответствующей текущему расположения «линейки», а также значения рассматриваемых характеристик на этой частоте.
В случае неверного ответа на этот и последующие вопросы на экране появляется сообщение об ошибке. Дальнейшая последовательность вопросов формируется, исходя из правильных ответов.
2) Находится ли замкнутая система на границе устойчивости (рис. 122)?
При совпадении значений и система находится на границе устойчивости. Аналогичный вывод следует, если эти частоты практически совпадают, то есть одновременно имеет место 
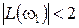дБ и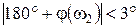 
.
Рис. 122.
Далее последовательность вопросов будет различаться. Рассмотрим основные варианты.
Система на границе устойчивости (типовые вопросы)
3) Сколько различных значений коэффициента передачи k обеспечивают границу устойчивости (рис. 123)?
Рис. 123.
Для ответа на этот вопрос мысленно перемещайте ЛАХ вверх или вниз и оцените возможность выполнения условий достижения границы устойчивости в других точках горизонтальной оси. Определите количество соответствующих положений ЛАХ.
4) Укажите другое, существенно отличающееся от заданного, значение k кр.
Порядок поиска критического значения коэффициента передачи рассмотрен выше в сведениях из теории к данной лабораторной работе.
Вопрос будет повторяться до получения точного ответа, после чего точка, соответствующая найденной границе устойчивости, будет отмечена маркером (рис. 124), и решение задачи завершено.
Рис.124.
Устойчивая система (типовые вопросы)
3) Устойчива ли замкнутая система (рис. 125)?
4) Система абсолютно или условно устойчива?
5) Можно ли достичь границы устойчивости увеличением коэффициента передачи?
6) Можно ли достичь границы устойчивости уменьшением коэффициента передачи?
7) Можно ли определить конечный запас устойчивости по амплитуде для увеличения k?
8) Можно ли определить конечный запас устойчивости по амплитуде для уменьшения k?
9) Определите запас устойчивости по амплитуде для увеличения (уменьшения) k (дБ).
В случае, когда для величины запрашиваемого запаса устойчивости можно дать более одного ответа, правильным является наименьшее значение.
Рис.125.
10) Можно ли определить запас устойчивости по фазе?
11) Определите запас устойчивости по фазе (град.).
Неустойчивая система (типовые вопросы)
3) Устойчива ли замкнутая система (рис. 126)?
4) Можно ли добиться устойчивости системы увеличением k?
5) Можно ли добиться устойчивости системы уменьшением k?
6) Укажите значение k, обеспечивающее границу устойчивости.
Рис. 126.
Вопрос будет повторяться до получения точного ответа, после чего точка, соответствующая найденной границе устойчивости, будет отмечена маркером, и решение задачи завершено.
4. Условием успешного выполнения работы является правильное решение пяти задач. Если в процессе решения задачи при ответе хотя бы на один вопрос допущена ошибка, ее потребуется решать повторно до получения правильных ответов на все вопросы. В зачет данная задача не идет (добавляется еще одна задача).
Контрольные вопросы
1. Какие характеристики системы используются для анализа устойчивости замкнутой системы с помощью критерия Найквиста?
2. Сформулируйте правила совместного построения ЛАХ и ЛФЧХ.
3. Что такое отрицательный и положительный переходы ЛФЧХ?
4. Что такое критический коэффициент передачи?
5. Как определить, находится ли система на границе устойчивости по графикам ЛАХ и ЛФЧХ?
6. Что такое частота среза?
7. Что такое запас устойчивости по амплитуде и как он определяется по логарифмическим частотным характеристикам?
8. Что такое запас устойчивости по фазе и как он определяется по логарифмическим частотным характеристикам?
9. Сформулируйте определение абсолютно и условно устойчивой системы.
10. Как рассчитать значение критического коэффициента передачи по логарифмическим частотным характеристикам?
Лабораторная работа № 7
|
|
|
