 |
Характеристики типовых динамических звеньев
|
|
|
|
Работа предлагается в двух версиях: стандартной и упрощенной. В упрощенной версии исключены весовые характеристики.
Стандартная версия – пакетный файл ДинЗв.bat, исполняемый файл tau121z.exe.
Упрощенная версия – пакетный файл ДинЗвУпр.bat, исполняемый файл tau120z.exe.
Выбор версии для выполнения производится по указанию преподавателя.
Сведения из теории
К типовым относят динамические звенья, которые с одной стороны достаточно просты и удобны для исследования, с другой стороны, обладают набором основных динамических свойств, характерных для звеньев и систем управления.
С точки зрения общности основных свойств типовые динамические звенья объединяют в три группы: позиционные, интегрирующие, дифференцирующие звенья.
Позиционные звенья
1. Безынерционное звено с передаточной функцией W (s)= k и уравнением x 2= kx 1
2. Апериодическое звено 1-го порядка с передаточной функцией 
и уравнением 
.
3. Апериодическое звено 2-го порядка с передаточной функцией 
и уравнением 
или 
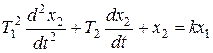при условии 
, обеспечивающем вещественные корни характеристического уравнения.
4. Колебательное звено с передаточной функцией 
и уравнением 
, где коэффициент демпфирования 
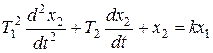или при условии 
, обеспечивающем комплексные корни характеристического уравнения.
5. Консервативное звено с передаточной функцией 
и уравнением 
- идеализация колебательного звена при коэффициенте демпфирования 
.
Интегрирующие звенья
6. Идеальное интегрирующее звено с передаточной функцией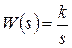 
и уравнением 
.
7. Интегрирующее звено с замедлением с передаточной функцией 
и уравнением 
.
8. Изодромное звено с передаточной функцией 
или 
и уравнением 
.
|
|
|
Дифференцирующие звенья
9. Идеальное дифференцирующее звено с передаточной функцией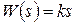 
и уравнением 
.
10. Дифференцирующее звено с замедлением с передаточной функцией 
и уравнением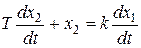 
.
Динамические свойства звеньев и систем наглядно отражаются временными и частотными характеристиками. Их определения, порядок и примеры получения рассмотрены в материалах практических занятий № 2-4. Рекомендуется в дополнение к материалам практических занятий получить временные и частотные характеристики типовых звеньев самостоятельно.
Анализ динамических свойств типовых звеньев, отражаемых АЧХ
Позиционные звенья
Рассмотрим сначала АЧХ апериодического звена первого порядка:
Рис.100.
(рис. 100).
Основной вывод, к которому приводит анализ данной характеристики, состоит в том, что инерционность динамического звена приводит к ослаблению пропускаемых высокочастотных сигналов тем больше, чем выше степень инерционности, характеризуемая величиной постоянной времени.
Теперь рассмотрим семейство АЧХ типовых позиционных динамических звеньев (рис. 101).
Рис.101.
На основе их сравнительного анализа можно сделать следующие выводы:
1. Общее свойство звеньев данной группы – пропорциональность выходного сигнала входному – присуще идеальному звену данной группы, безынерционному (1), независимо от частоты входного сигнала.
2. Следствием инерционности остальных звеньев является ухудшение пропускания гармонических сигналов по мере увеличения их частоты. При этом в зависимости от характера инерционности это свойство проявляется по разному.
У апериодических звеньев 1-го (2) и 2-го порядка (3) степень ослабления гармонического сигнала растет монотонно.
У колебательного (4) и консервативного (5) звеньев этот же эффект наблюдается на частотах выше резонансной.
Интегрирующие звенья
На рис. 102 показано семейство АЧХ типовых интегрирующих динамических звеньев.
|
|
|
Рис.102.
Общие свойства звеньев данной группы наглядно иллюстрируются АЧХ идеального интегрирующего (6) и интегрирующего с замедлением (7) звеньев – усиление сигналов низких частот и подавление высокочастотных сигналов. На высоких частотах динамические свойства интегрирующих звеньев резко ухудшаются, пропускная способность с увеличением частоты падает до нуля.
Улучшенные динамические свойства изодромного звена проявляются в том, что на низких частотах оно ведет себя как интегрирующее, усиливая низкочастотные сигналы, а на высоких – как безынерционное, сохраняя пропускную способность для высокочастотных сигналов.
Дифференцирующие звенья
Приведенные на рис. 103 АЧХ типовых дифференцирующих звеньев показывают, что они обладают наилучшими динамическими свойствами по сравнению с двумя рассмотренными выше группами. Дифференцирующие звенья лучше пропускают высокочастотные сигналы, подавляя низкочастотные. Это в наибольшей степени характерно для идеального дифференцирующего звена (9). Инерционность дифференцирующего звена с замедлением (10) ограничивает возможности усиления высокочастотных сигналов.
Рис.103.
Следует отметить, что побочным отрицательным эффектом таких динамических свойств может быть низкая помехозащищенность систем, содержащих дифференцирующие звенья и подверженных влиянию шумовых (с ярко выраженной высокочастотной составляющей) помех.
Анализ динамических свойств типовых звеньев, отражаемых ФЧХ
Позиционные звенья
На рис. 104 показано семейство ФЧХ типовых позиционных звеньев.
Рис.104.
Общее свойство звеньев данной группы – масштабирование входного сигнала – не вызывает внесения фазового сдвига в преобразуемый сигнал, что и демонстрирует ФЧХ безынерционного звена (1). Инерционность остальных звеньев данной группы определяет отрицательный фазовый сдвиг, возрастающий с увеличением частоты. Порядок инерционности определяет диапазон изменения фазового сдвига: до -90° у апериодического звена 1-го порядка (2), до -180° у остальных звеньев данной группы.
Интегрирующие звенья
Семейство их ФЧХ показано на рис. 105.
Все интегрирующие звенья вносят в преобразуемый сигнал отрицательный фазовый сдвиг, обусловленный выполняемой операцией интегрирования сигнала. Об этом непосредственно свидетельствует ФЧХ идеального интегрирующего звена (6). Инерционность интегрирующего звена с замедлением (7) определяет увеличение вносимого им отрицательного фазового сдвига по мере увеличения частоты преобразуемого сигнала. Улучшенные динамические свойства изодромного звена (8) здесь проявляются в форме снижения вносимого им отрицательного фазового сдвига по мере увеличения частоты.
|
|
|
Рис.105. Рис.106.
Дифференцирующие звенья
Противоположные динамические свойства демонстрируют фазо-частотные характеристики дифференцирующих звеньев (рис. 106).
Выполняя операцию дифференцирования, звенья этой группы вносят в преобразуемый сигнал положительный фазовый сдвиг. Однократное дифференцирование (9) определяет фазовый сдвиг +90°. Инерционность дифференцирующего звена с замедлением (10) определяет снижение положительного фазового сдвига с увеличением частоты.
Анализ динамических свойств типовых звеньев, отражаемых
переходной характеристикой
Позиционные звенья
Рис.107.
На рис. 107 показаны переходные характеристики типовых позиционных звеньев.
На основе их сравнительного анализа можно сделать следующие выводы:
1. Общим свойством звеньев данной группы является пропорциональность выходного сигнала входному, обеспечиваемая по окончании переходного процесса. Именно это свойство является единственным для идеального звена данной группы – безынерционного (1).
2. Общее отличие всех звеньев от безынерционного состоит в наличии переходного процесса, вызванного их инерционностью. Различия же между звеньями внутри группы определяются количеством и соотношением постоянных времени, то есть характером инерционности.
Так, процесс в звеньях второго порядка – апериодическом 2-го порядка (3), колебательном (4) и консервативном(5) – в отличие от апериодического звена 1-го порядка (2), начинает развиваться не мгновенно, так как здесь и начальная скорость изменения сигнала – нулевая.
|
|
|
Интегрирующие звенья
Рис. 108.
На рис. 108 показаны переходные характеристики типовых интегрирующих звеньев.
На основе их сравнительного анализа можно сделать следующие выводы:
1. Общее свойство звеньев данной группы отражается характеристикой идеального интегрирующего звена (6) – в установившемся процессе выходной сигнал пропорционален интегралу от входного.
2. У остальных звеньев данной группы проявляются дополнительные динамические свойства: инерционность у интегрирующего звена с замедлением (7) и противоположный эффект у изодромного звена (8), приводящий к тому, что процесс в данном звене ускоряется по сравнению с процессом в идеальном звене. Формально такая разница в динамических свойствах отражается расположением постоянной времени в передаточной функции: в знаменателе при наличии инерционности и в числителе в противоположном случае.
Дифференцирующие звенья
На рис. 109 показаны переходные характеристики типовых дифференцирующих звеньев.
На основе их сравнительного анализа можно сделать следующие выводы:
Рис.109
1. Общее свойство звеньев данной группы отражается характеристикой идеального дифференцирующего звена (9) – в установившемся процессе выходной сигнал пропорционален производной входного.
2. Наличие инерционности у дифференцирующего звена с замедлением (10) приводит к переходному процессу.
Полный перечень характеристик типовых динамических звеньев представлен в [1].
Порядок выполнения работы
1. После запуска пакетного файла ознакомьтесь с информацией на заставке программы (рис. 110) и снимите ее нажатием любой клавиши.
Рис.110.
2. Внимательно изучите справочную информацию и инструкции на экране (рис. 111). Следуйте инструкциям о порядке использования клавиш в процессе выполнения работы.
Рис.111.
3. Для заданного динамического звена необходимо подобрать график требуемой характеристики.
В лабораторной работе рассматриваются следующие характеристики:
1) амплитудно-частотная характеристика АЧХ A (ω);
2) фазо-частотная характеристика ФЧХ φ (ω);
3) амплитудно-фазовая характеристика (годограф) АФХ;
4) логарифмическая амплитудная характеристика ЛАХ L (ω);
5) переходная характеристика h (t);
6) весовая характеристика w (t).
4. Условием успешного выполнения работы является правильный подбор десяти характеристик подряд. Информация о количестве правильных ответов размещается в нижней части экрана. В случае ошибки при подборе очередной характеристики счетчик оставшихся до зачета вопросов устанавливается в исходное значение 10, и выполнение работы должно быть продолжено.
|
|
|
При ошибочном ответе программа указывает правильный вариант.
Контрольные вопросы
1. Назовите основные группы динамических звеньев.
2. Какие основные свойства присущи этим группам?
3. Назовите типовые динамические звенья для каждой из групп.
4. Приведите примеры технической реализации этих звеньев.
5. Перечислите временные характеристики динамических звеньев.
6. Перечислите частотные характеристики динамических звеньев.
7. Как влияет инерционность динамического звена на величину пропускаемых высокочастотных сигналов?
8. Как ведут себя дифференцирующие звенья в условиях шумовых помех?
9. К какому фазовому сдвигу приводит инерционность позиционных звеньев?
10. Какой фазовый сдвиг вносят интегрирующие звенья в преобразуемый сигнал?
11. Какой фазовый сдвиг вносят дифференцирующие звенья в преобразуемый сигнал?
12. Перечислите принципиальные различия в динамических свойствах интегрирующих и дифференцирующих звеньев. Как они проявляются на рассмотренных характеристиках: переходных, АЧХ, ФЧХ?
13. Какое общее свойство можно обнаружить по переходным характеристикам для:
- позиционных звеньев;
- интегрирующих звеньев;
- дифференцирующих звеньев.
Лабораторная работа № 5
|
|
|
