Угловые кинематические характеристики

Всякое твердое тело можно представить в виде совокупности бесконечно большого числа материальных точек. Если не учитывать деформации, то можно говорить об абсолютно твердом теле, то есть о системе материальных точек, расстояния между которыми остаются неизменными. При вращении абсолютно твердого тела вокруг неподвижной оси все его точки описывают окружности. Линейные скорости этих точек различны, но угловая скорость для всех точек одинакова и поэтому может характеризовать движение всего тела. Для простоты будем говорить о движении, происходящем в одной плоскости (например, в плоскости 0 XY декартовой системы координат). Положение точки на окружности можно задать углом поворота Δφ радиус-вектора r, соединяющего ее с центром вращения, выбранным в качестве начала координат, по отношению к направлению оси Х. Чтобы с помощью элементарного угла Δφ определить не только изменение положения, но и направление движения материальной точки, введем псевдовектор Δ φ. Ему приписывается направление, перпендикулярное плоскости, в которой лежит дуга ΔS, по которой движется точка. Направление вектора Δ φ определяется правилом буравчика (правого винта): вращение рукоятки буравчика совпадает с движением точки, а поступательное движение буравчика указывает направление вектора Δ φ. Определим далее угловую скорость и угловое ускорение. Угловой скоростью называется вектор ω = d φ / dt. Численно угловая скорость ω равна углу поворота радиус-вектора точки в единицу времени, или углу поворота тела в единицу времени, если речь идет о вращении тела. Направлена угловая скорость по оси вращения. Угловое ускорение – это быстрота изменения угловой скорости. Его определяют из соотношения ε = d ω / dt. Угловое ускорение находят как вторую производную от угла поворота радиус-вектора по времени. При ускоренном движении направление вектора углового ускорения совпадает с направлением угловой скорости. При замедленном – противоположное. Линейные и угловые кинематические характеристики точки, движущейся по окружности, связаны между собой простыми соотношениями. Для модулей рассматриваемых величин эти соотношения имеют вид

            S = R φ; V = R ω; a = R ε.

Угловое перемещение φ измеряется в радианах. Угол, измеренный в радианах, находится через отношение стягивающей его дуги к ее радиусу. Радиан – безразмерная величина. Таким образом, размерность угловой скорости, будет с^-1, а размерность углового ускорения – с^-2. 

Динамика материальной точки

Законы Ньютона

Динамика изучает движение тел с учетом причин, вызвавших это движение. Основой классической механики являются законы Ньютона, сформулированные в результате обобщения большого количества экспериментальных фактов.

    Первый закон Ньютона: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить этого состояния.

Ускорение , если действующая на тело результирующая сила .

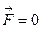    Второй закон Ньютона: скорость изменения результирующего импульса тела  равна действующей на тело результирующей силе :

.

Это уравнение еще называют законом движения. Поскольку импульс тела , где  – масса тела, а  – скорость, для тела постоянной массы возможен другой вариант записи второго закона Ньютона:                               

                   .

    Третий закон Ньютона: Силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению:            

.

Обратите внимание, что здесь речь идет о силах, приложенных к различным телам.

Импульс силы   позволяет вычислять величину сил реакции, возникающих при соударении. Импульс силы можно связать с изменением импульса тела, воспользовавшись вторым законом Ньютона и записав его следующим образом:

 .