 |
3. Способы задания кривых поверхностей на чертеже.
|
|
|
|
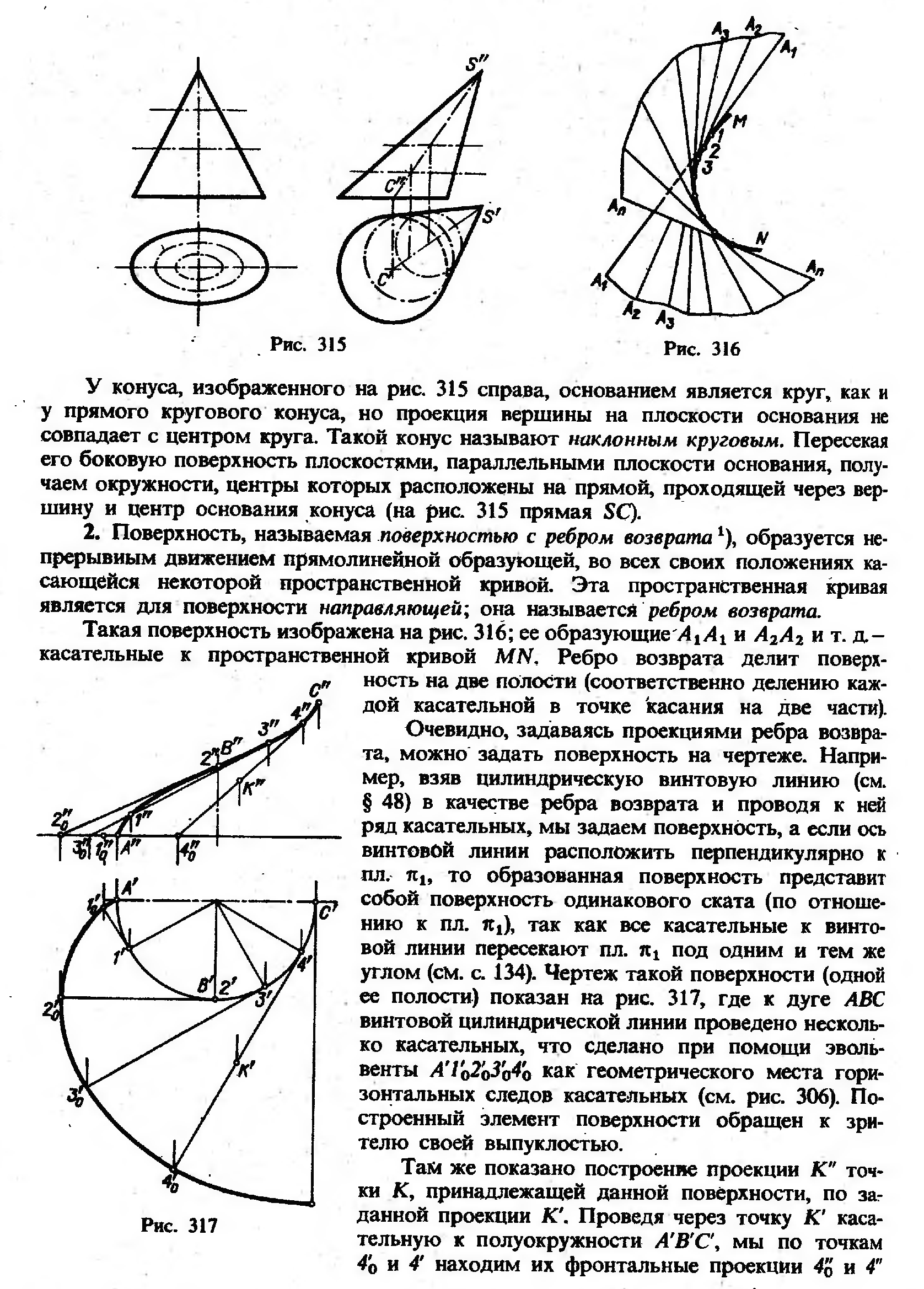
3. СПОСОБЫ ЗАДАНИЯ КРИВЫХ ПОВЕРХНОСТЕЙ НА ЧЕРТЕЖЕ.
Билет №14
1. ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ ОТ ТОЧКИ ДО ПЛОСКОСТИ.
Для определения расстояния от точки до плоскости необходимо из точки опустить перпендикуляр на плоскость. Известно, что прямая перпендикулярна плоскости, если она перпендикулярна любым двум пересекающимся прямым, принадлежащим плоскости. При этом перпендикуляр может не проходить через точку пересечения прямых, а скрещиваться с ними. Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на эту плоскость.
Алгоритм построения:
· Строится перпендикуляр из точки K на плоскость s (АВС): m1 h1, m2 f2.
· Находится точка N – точка пересечения перпендикуляра m с плоскостью s (АВС).
· Определяется расстояние от точки K до точки N с помощью прямоугольного треугольника K1N1M0. Длина гипотенузы N1M0 – это искомое расстояние: |KN| = N1M0.
Расстояние между параллельными плоскостями определяется длиной перпендикуляра, опущенного из произвольной точки одной плоскости до другой. Аналогично находится расстояние от плоскости до параллельной ей прямой. На прямой берется точка и находится расстояние до плоскости.
Все задачи на определение расстояний, углов, площадей, построение точек, прямых, плоских фигур по заданным параметрам могут быть решены на основе трех основных задач: построение перпендикуляра к плоскости, определение длины отрезка общего положения и построение точки пересечения прямой с плоскостью.
2. СЕЧЕНИЕ КРИВОЙ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ.
Билет № 17
1. ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ; ПАРАЛЛЕЛЬНОСТЬ ДВУХ ПЛОСКОСТЕЙ.
|
|
|
Определение . Прямая и плоскость называются параллельными, если они не имеют общих точек (а||α )
Признак параллельности прямой и плоскости.
Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.
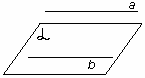
Рис 21.
Замечания.
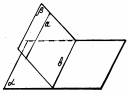Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Рис22.
Если одна из двух параллельных прямых параллельна данной плоскости, а другая прямая имеет с плоскостью общую точку, то эта прямая лежит в данной плоскости.
Выводы.
Случаи взаимного расположения прямой и плоскости:
а) прямая лежит в плоскости;
б) прямая и плоскость имеют только одну общую точку;
в) прямая и плоскость не имеют ни одной общей точки.
Определение. Две плоскости называются параллельными, если они не имеют общих точек.
Рис23
Параллельность плоскостей и обозначается так: ||. Рассмотрим признак параллельности двух плоскостей.
Теорема. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Случаи взаимного расположения плоскостей:
Плоскости α и β пересекаются.
Рис 24
плоскости α и β параллельны
Рис 25
Свойства параллельных плоскостей:
1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Рис 26
2. Отрезки параллельных прямых, заключённые между параллельными
плоскостями, равны.
Рис 26 а
|
|
|
2. РАЗВЕРТКА МНОГОГРАННИКА, МЕТОД РАСКАТКИ.
Разверткой многогранника называется плоская фигура, получаемая последовательным совмещением всех граней поверхности с плоскостью.
Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, ее построение сводится к определению величины отдельных граней поверхности – плоских многоугольников.
Существует три метода построения развертки многогранных поверхностей:
1. Метод треугольника.
2. Метод нормального сечения.
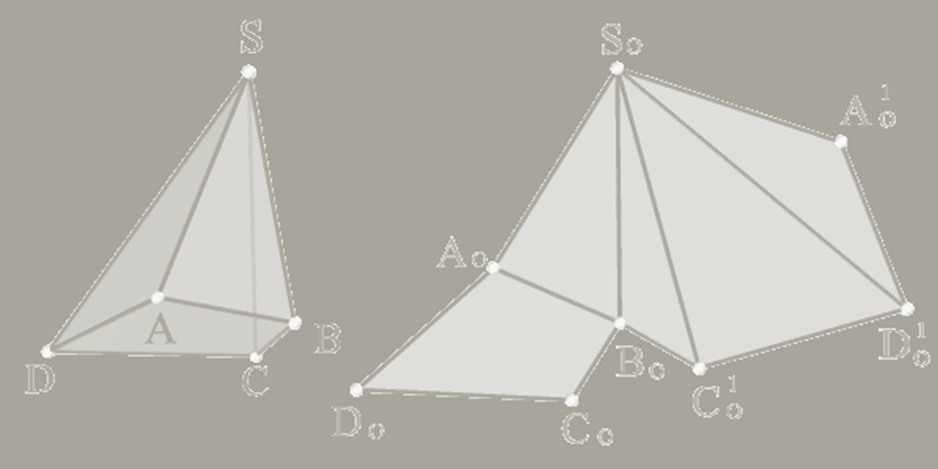3. Метод раскатки.
Способ раскатки целесообразно использовать для построения развёртки поверхности призмы, основание которой параллельно какой-либо плоскости проекций, а рёбра — параллельны другой плоскости проекций.
|
|
|
