 |
I. Положение прямой относительно плоскостей проекций, прямые частного положения.
|
|
|
|
Билет № 4.
I. ПОЛОЖЕНИЕ ПРЯМОЙ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ, ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ.
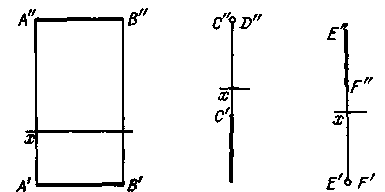
А. Прямая параллельна одной плоскости проекций.
1). Прямая параллельна пл. π 1. рис 50. В таком случае фронтальная проекция прямой параллельна оси проекций и горизонтальная проекция отрезка этой прямой равна самому отрезку: А’В’ = АВ. Такая прямая называется горизонтальной.
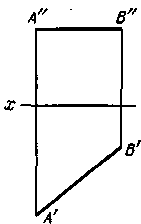Если, например, проекция А”В” совпадает с осью проекций, то отрезок АВ расположен в пл. π 1.
Рис. 50
2). Прямая параллельна пл. π 2. рис 51. В таком случае ее горизонтальная проекция параллельна оси проекций и фронтальная проекция отрезка этой прямой равна самому отрезку: C”D” = CD. Такая прямая называется фронтальной.
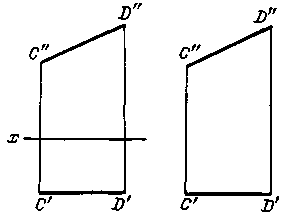Если, например, проекция C’D’ совпадает с осью проекций, то это соответствует положению отрезка CD в самой пл. π 2.
Рис. 51
3). Прямая параллельна пл. π 3. В таком случае горизонтальная и фронтальная проекции прямой располагаются на одном перпендикуляре к оси проекций Ох и профильная проекция этой прямой равна самому отрезку E”F” = EF. Такая прямая называется профильной.
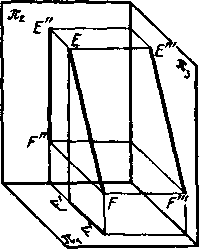
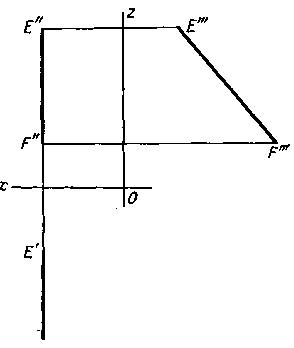Если же на чертеже в системе π 1 и π 2 обе проекции перпендикулярны к оси проекций, то проецирующие плоскости, проведенные через E’F’ и E”F”, сливаются в одну и оригиналом может быть не только прямая линия, но и некоторая плоская кривая.
|
|
|
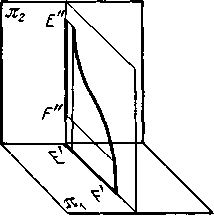
Рис. 52 рис. 53
Б. Прямая параллельна двум плоскостям проекций.
1). Прямая параллельна плоскостям π 1 и π 2, т. е. перпендикулярна к пл. π 3. Проекция на пл. π 3 представит собой точку.
2). Прямая параллельна плоскостям π 1 и π 3, т. е. перпендикулярна к пл. π 2. Проекция на пл. π 3 представляет собой отрезок прямой, равный C’D’.
рис. 54 рис. 55 рис. 56 рис. 57
3). Прямая параллельна плоскостям π 2 и π 3, т. е. перпендикулярна к пл. π 1. Проекция на пл. π 3 представит собой отрезок, параллельный и равный E”F”.
Рис. 58 рис. 59
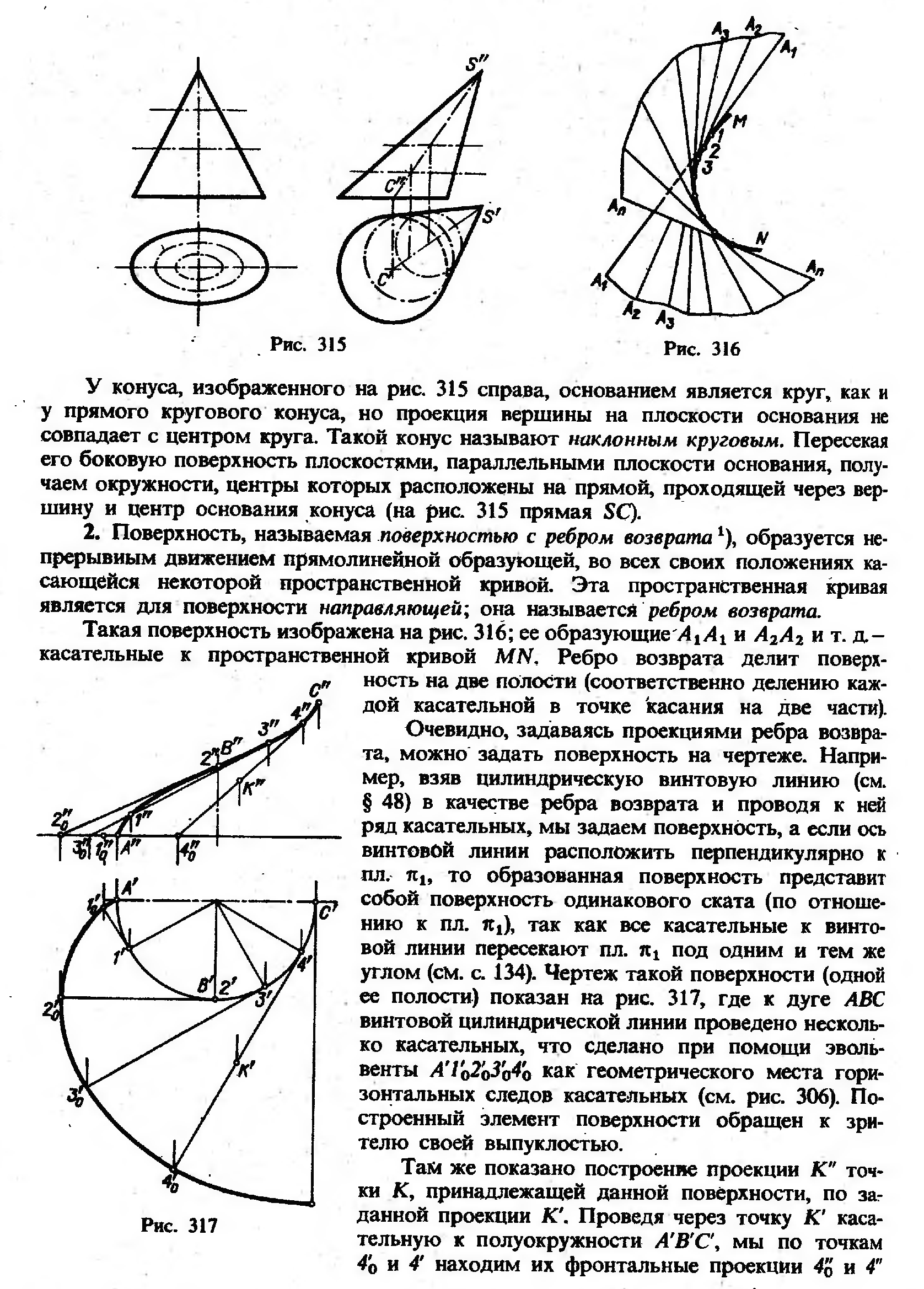
II. СПОСОБЫ ЗАДАНИЯ КРИВЫХ ПОВЕРХНОСТЕЙ НА ЧЕРТЕЖЕ.
Билет № 5
1. ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯ, ПОСТОЕНИЕ СЛЕДОВ ПРЯМОЙ.
А, Прямая общего положения – это прямая не параллельная не одной плоскости проекции. Любой отрезок такой прямой проецируется в данной системе плоскостей проекций искаженно. Искаженно проецируются и углы наклона этой прямой к плоскостям проекций.
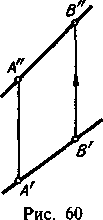
Рис 65 рис 66
Б, Построение следов прямой
На рис. 65 показаны точки M и N, в которых прямая, заданная отрезком АВ, пересекает плоскости проекций. Эти точки называются следами: точка M -- горизонтальный след прямой, точка N -- ее фронтальный след.
|
|
|
Горизонтальная проекция горизонтального следа (точка М') совпадает с самим следом, а фронтальная проекция этого следа М" лежит на оси проекций. Фронтальная проекция фронтального следа N" совпадает с точкой N, а горизонтальная проекция N ' лежит на той же оси проекций.
Следовательно, чтобы найти горизонтальный след, надо (рис. 66) продолжить фронтальную проекцию А" В" до пересечения с осью П2/П1 и через точку М" (фронтальную проекцию горизонтального следа) провести перпендикуляр к оси П2/П1 до пересечения с продолжением горизонтальной проекции А'В'. Точка М' -- горизонтальная проекция горизонтального следа; она совпадает с самим следом (= знак совпадения).
Для нахождения фронтального следа продолжаем горизонтальную проекцию А'В' до пересечения с П2/П1; через точку N' (горизонтальную проекцию фронтального следа) проводим перпендикуляр до пересечения с продолжением фронтальной проекции А" В". Точка N" -- фронтальная проекция фронтального следа; она совпадает с самим следом. Прямая не имеет следа на плоскости проекций в том случае, когда она параллельна этой плоскости. На рис. 67 прямая пересекает не только пл. П1 и П2, но и пл. П3. Точка Р -- профильный след прямой, т. е. след на профильной плоскости проекций. Этот след совпадает с его собственной проекцией на пл. П3, а фронтальная и горизонтальная проекции его лежат соответственно на осях z и у.
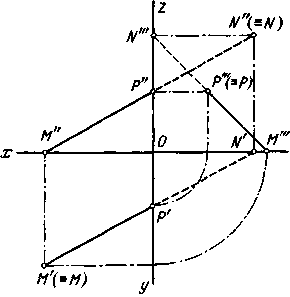
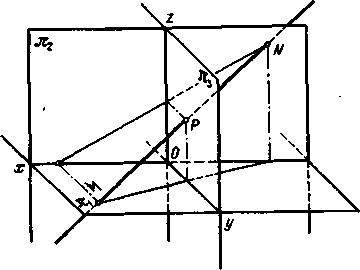
Рис 67
|
|
|
