 |
1. Построение развертки многогранников, способ триангуляции.
|
|
|
|
Билет №10
1. ПОСТРОЕНИЕ РАЗВЕРТКИ МНОГОГРАННИКОВ, СПОСОБ ТРИАНГУЛЯЦИИ.
Развертка – совмещенная с плоскостью поверхность многогранника без разрывов. Развёртка многогранной поверхности – плоская фигура, полученная в результате последовательного совмещения всех её граней с плоскостью.
Развёртка пирамиды. Способ триангуляции.
Сущность способа заключается в нахождении Н. В. всех рёбер пирамиды и построении на плоскости контуров боковых граней (треугольников), которые последовательно соединяют друг с другом смежными рёбрами. К ним присоединяется основание пирамиды.
В данном примере Н. В. рёбер определяем способом вращения вокруг проецирующей оси, которая проходит через вершину пирамиды.
Точка К – произвольная точка.
1. Находим Н. В. каждого из рёбер пирамиды;
2. Строим треугольники на развёртке методом засечек;
3. Основание пирамиды – треугольник АВС на П1 спроецирован в натуральную величину. Пристраиваем основание к ребру СА.
2. СПОСОБЫ ОПРЕДЕЛЕНИЯ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ ПЛОСКОЙ ФИГУРЫ.
Определение истинной величины плоской фигуры можно осуществить путем преобразования чертежа способом замены плоскостей проекций. На рис. 146, а дан комплексный чертеж прямоугольника ABCD. Ни одна из проекций прямоугольника не занимает частного положения. Задачу решаем последовательным решением третьей и четвертой основных задач. Заменив плоскость П2 на П4, приводим прямоугольник в частное положение, т. е. в виде проецирующей по отношению к П4 – Выполнив вторую замену, то есть замену П4 на П5, определяем истинную величину прямоугольника ABC.
Рис. 146 Определение натуральной величины плоской фигуры
|
|
|
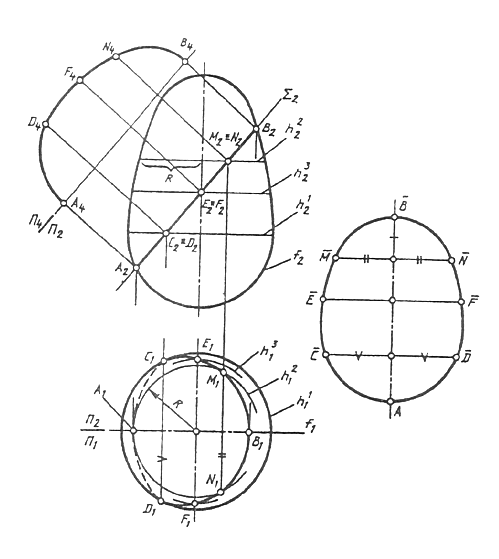Задачу определения истинной величины прямоугольника можно также решить способом вращения вокруг линии уровня плоскости этой фигуры до совмещения с соответствующей плоскостью уровня (рис. 146, б). В ряду рассматриваемых задач может быть также решена задача на определение истинной величины фигуры сечения поверхности проецирующей плоскостью. В этом случае достаточно одной замены плоскостей проекций (исходная задача 3). В этом случае истинную величину фигуры сечения можно легко построить путем непосредственного замера расстояний точек фигуры «вдоль сечения» и «поперек сечения» (рис. 147).
Рис. 147 Построение путем непосредственного замера расстояний
Длина фигуры сечения АВ изображается в истинную величину на плоскости П2, так как является отрезком фигуры фронтали секущей плоскости. Расстояние между симметричными точками «поперек сечения» изображается в натуральную величину на плоскости П1 так как является отрезками горизонталей секущей плоскости
Билет № 11
1. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ, ОПРЕДЕЛЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПЛОСКОСТЕЙ.
Две плоскости в пространстве могут быть либо взаимно параллельны, в частном случае совпадая друг с другом, либо пересекаться. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей.
1) Параллельные плоскости. Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Это определение хорошо иллюстрируется задачей, через точку В провести плоскость параллельную плоскости, заданной двумя пересекающимися прямыми ab (рис. 7. 1). Задача. Дано: плоскость общего положения, заданную двумя пересекающимися прямыми ab и точка В. Требуется через точку В провести плоскость, параллельную плоскости ab и задать её двумя пересекающимися прямыми c и d. Согласно определения если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости то эти плоскости параллельны между собой. Для того чтобы провести на эпюре параллельные прямые необходимо воспользоваться свойством параллельного проецирования – проекции параллельных прямых – параллельны между собой d||a, с||b; d1||a1, с1||b1; d2||a2, с2||b2; d3||a3, с3||b3.
|
|
|
2) Пересекающиеся плоскости, частный случай – взаимно перпендикулярные плоскости. Линия пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей. Рассмотрим построение линии пересечения двух плоскостей, когда одна из них проецирующая (рис. 7. 2).
Рис 7. 1 рис 7. 2 рис 7. 3
Рисунок 7. 1 – Параллельные плоскости
Рисунок 7. 2 – Пересечение плоскости общего положения с горизонтально проецирующей плоскостью
Рисунок 7. 3 – Пересечение плоскостей общего положения
Рисунок 7. 4 – Взаимно перпендикулярные плоскости
Некоторого упрощения при построении линии пересечения плоскостей можно достичь, если вспомогательные секущие плоскости проводить через прямые, задающие плоскость.
Взаимно перпендикулярные плоскости. Из стереометрии известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.
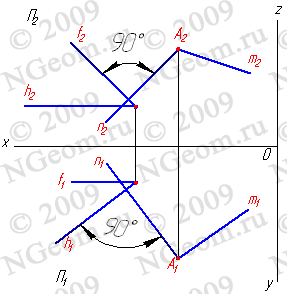
Рис 7. 4
|
|
|
