 |
2. Построение проекций сечения кривой поверхности плоскостью.
|
|
|
|
2. Построение проекций сечения кривой поверхности плоскостью.
Плоскостью, известна и ее проекции могут быть построены на основании их геометрических свойств.
Билет № 6
1. ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯ, ПОСТОЕНИЕ СЛЕДОВ ПРЯМОЙ.
А, Прямая общего положения – это прямая не параллельная не одной плоскости проекции. Любой отрезок такой прямой проецируется в данной системе плоскостей проекций искаженно. Искаженно проецируются и углы наклона этой прямой к плоскостям проекций.
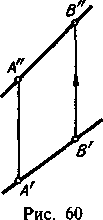
Рис 65 рис 66
Б, Построение следов прямой
На рис. 65 показаны точки M и N, в которых прямая, заданная отрезком АВ, пересекает плоскости проекций. Эти точки называются следами: точка M – горизонтальный след прямой, точка N – ее фронтальный след.
Горизонтальная проекция горизонтального следа (точка М') совпадает с самим следом, а фронтальная проекция этого следа М» лежит на оси проекций. Фронтальная проекция фронтального следа N» совпадает с точкой N, а горизонтальная проекция N ' лежит на той же оси проекций.
Следовательно, чтобы найти горизонтальный след, надо (рис. 66) продолжить фронтальную проекцию А»В» до пересечения с осью П2/П1 и через точку М» (фронтальную проекцию горизонтального следа) провести перпендикуляр к оси П2/П1 до пересечения с продолжением горизонтальной проекции А'В'. Точка М' -- горизонтальная проекция горизонтального следа; она совпадает с самим следом (= знак совпадения).
|
|
|
Для нахождения фронтального следа продолжаем горизонтальную проекцию А'В' до пересечения с П2/П1; через точку N' (горизонтальную проекцию фронтального следа) проводим перпендикуляр до пересечения с продолжением фронтальной проекции А»В». Точка N»–фронтальная проекция фронтального следа; она совпадает с самим следом. Прямая не имеет следа на плоскости проекций в том случае, когда она параллельна этой плоскости. На рис. 67 прямая пересекает не только пл. П1 и П2, но и пл. П3. Точка Р -- профильный след прямой, т. е. след на профильной плоскости проекций. Этот след совпадает с его собственной проекцией на пл. П3, а фронтальная и горизонтальная проекции его лежат соответственно на осях z и у.
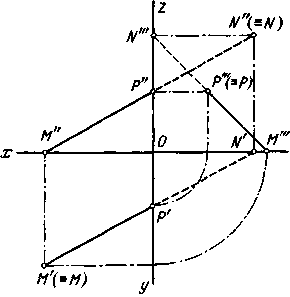
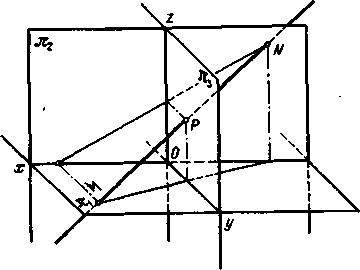
Рис 67
2. СПОСОБ ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ ПЛОСКОСТЕЙ ПРИ ПОСТРОЕНИИ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ.
При построении линии пересечения поверхностей особенности пересечения соосных поверхностей вращения позволяют в качестве вспомогательных поверхностей-посредников использовать сферы, с данными поверхностями.
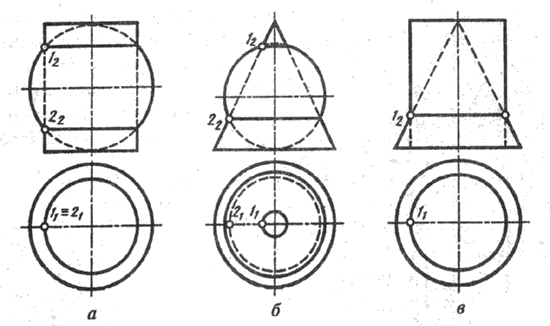
К поверхностям вращения относятся поверхности, имеющие общую ось вращения. На рис. 134 изображены цилиндр и сфера (рис. 134, а), конус и сфера (рис. 134, б) и цилиндр и конус (рис. 134, в).
Поверхности вращения всегда пересекаются по окружностям, плоскости которых перпендикулярны оси вращения. Этих общих для обеих поверхностей окружностей столько, сколько существует точек пересечения очерковых линий поверхностей. Поверхности на рис. 134 пересекаются по окружностям, создаваемым точками 1 и 2 пересечения их главных меридианов.
Вспомогательная сфера-посредник пересекает каждую из заданных поверхностей по окружности, в пересечении которых получаются точки, принадлежащие и другой поверхности, а значит, и линии пересечения.
|
|
|
Рис. 134
Если оси поверхностей пересекаются, то вспомогательные сферы проводят из одного центра-точки пересечения осей. Линию пересечения поверхностей в этом случае строят способом вспомогательных концентрических сфер.
При построении линии пересечения поверхностей для использования способа вспомогательных концентрических сфер необходимо выполнение следующих условий:
· пересечение поверхностей вращения;
· оси поверхностей – пересекающиеся прямые – параллельны одной из плоскостей проекций, т. е. имеется общая плоскость симметрии;
· нельзя использовать способ вспомогательных секущих плоскостей, так как они не дают графически простых линий на поверхностях.
Обычно способ вспомогательных сфер используется в сочетании со способом вспомогательных секущих плоскостей. На рис. 135 построена линия пересечения двух конических поверхностей вращения с пересекающимися во фронтальной плоскости уровня Ф (Ф1) осями вращения. Значит, главные меридианы этих поверхностей пересекаются и дают в своем пересечении точки видимости линии пересечения относительно плоскости П2 или самую высокую А и самую низкую В точки. В пересечении горизонтального меридиана h и параллели h', лежащих в одной вспомогательной секущей плоскости Г(Г2), определены точки видимости С и D линии пересечения относительно плоскости П1. Использовать вспомогательные секущие плоскости для построения дополнительных точек линии пересечения нецелесообразно, так как плоскости, параллельные Ф, будут пересекать обе поверхности по гиперболам, а плоскости, параллельные Г, будут давать в пересечении поверхностей окружности и гиперболы.
|
|
|
