 |
2. Преобразование проекций, плоско–параллельное перемещение.
|
|
|
|
2. ПРЕОБРАЗОВАНИЕ ПРОЕКЦИЙ, ПЛОСКО–ПАРАЛЛЕЛЬНОЕ ПЕРЕМЕЩЕНИЕ.
Преобразование проекций используется для наиболее выгодного изображения геометрических фигур при их исследовании и решение методических и позиционных задач. В итоге при преобразовании чертежа объекты занимают частное положение относительно плоскостей проекций. Существуют несколько способов преобразования.
- способ замены плоскостей проекций.
- способ вращения вокруг проецирующих прямых и прямых уровня.
- способ плоскопараллельного перемещения.
Принципиальная разница первого способа (замены плоскостей проекций) в том, что объект не меняет своего положения в пространстве, а вводятся новые дополнительные плоскости проекций. При использовании способов вращения и плоскопараллельного перемещения – система плоскостей остаётся неизменной, а объект перемещается относительно системы плоскостей.
Способ плоскопараллельного перемещения основан на том, что при параллельном переносе геометрического тела относительно плоскости проекций проекция его на эту плоскость не меняет своей формы и размеров, хотя и меняет положение. При этом если точка перемещается в плоскости, параллельной П1, то ее фронтальная проекция изображается в виде прямой, параллельной оси П2/П1. Если же точка перемещается в плоскости, параллельной П2, то ее горизонтальная проекция изображается в виде прямой, параллельной той же оси.

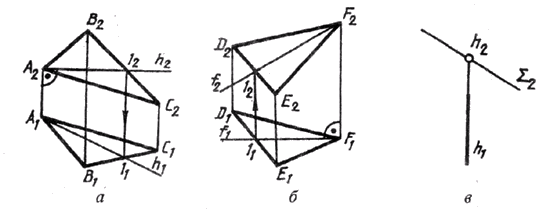
На рис. 107 показан комплексный чертеж прямой АВ. Прямая не параллельна ни одной из плоскостей проекций. Требуется с помощью плоскопараллельного перемещения задать ей такое положение, чтобы она была параллельна одной из плоскостей проекций, например П2. Через произвольную точку А1, проводим прямую l1 параллельную оси П2/П1, и от этой точки на прямой откладываем отрезок, равный А1В1. Из точки А1 проводим вертикальную линию связи, а из точки AT, — горизонтальную линию, на пересечении которых и будет новое положение фронтальной проекции А2'. Аналогично проведем вертикальную линию связи из точки В1 до пересечения с горизонтальной линией, проведенной из точки B2. Новое положение фронтальной проекции точки В получим на пересечении этих линий в точке В2'.
|
|
|
После преобразования чертежа горизонтальная проекция прямой АВ стала параллельна плоскости П2, а значит, спроецировалась она на эту плоскость в натуральную величину.
Применяя метод плоскопараллельного перемещения, можно решать многие задачи, связанные с определением натуральной величины отрезков, углов, плоских фигур, а также заданием им нужного положения. Однако он связан с изменением положения геометрической фигуры в пространстве. В практике же встречаются задачи, при решении которых при преобразовании комплексного чертежа удобнее оставить положение проецирующего тела неизменным, а изменить положение плоскостей проекций.
Билет № 12
1. ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ.
Прямые уровня – это прямые, принадлежащие плоскости и параллельные какай – либо плоскости проекций. Эти прямые называют прямыми уровня, так как они принадлежат плоскости уровня. Существует три вида прямых уровня:
· h – горизонталь плоскости – прямая принадлежащая данной плоскости и || П1;
· f – фронталь плоскости – прямая принадлежащая данной плоскости и || П2;
· w – профильная прямая плоскости – прямая принадлежащая данной плоскости и || П3.
Рассмотрим построение прямой уровня на примере горизонтали. Возьмем плоскость ABC общего положения. Искомая прямая параллельна плоскости П1 а это значит, что ее проекция на П2 будет горизонтальной линией. Нарисуем эту проекцию в любом месте. В любом потому, что горизонталей у плоскости бесконечное количество, а нам не имеет значения, какую из них строить. Найдем точки пересечения K2 и L2 со сторонами треугольника ABC. Опустив линии связи находим вторые проекции K1 и L1 и достраиваем вторую проекцию горизонтали.
|
|
|
2.
|
|
|


