 |
1. Взаимно – перпендикулярные плоскости. Общий алгоритм
|
|
|
|
Билет №7
1. ВЗАИМНО – ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ. ОБЩИЙ АЛГОРИТМ
ПОСТРОЕНИЯ ВЗАИМНО – ПЕРПЕНДИКУЛЯРНЫХ ПЛОСКОСТЕЙ.
Взаимно – перпендикулярные прямые – это те прямые, если угол между ними равен девяноста градусам.
Построение плоскости β , перпендикулярной к плоскости α, может быть произведено двумя путями: 1) пл. β проводится через прямую, перпендикулярную к пл. а; 2) пл. проводится перпендикулярно к прямой, лежащей в пл. α или параллельной этой плоскости. Для получения единственного решения требуются дополнительные условия.
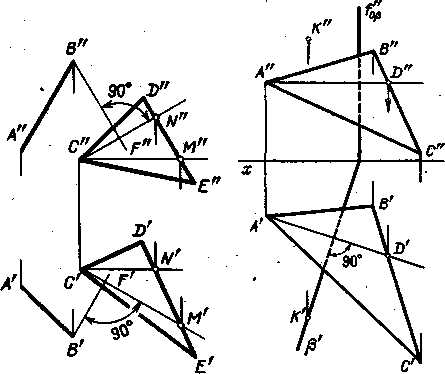На рис. 193 показано построение плоскости, перпендикулярной к плоскости, заданной треугольником CDE. Дополнительным условием здесь служит то, что искомая плоскость должна проходить через прямую АВ. Следовательно, искомая плоскость определяется прямой АВ и перпендикуляром к плоскости треугольника.
Рис 193 рис 194
Итак, перпендикулярность горизонтальных следов плоскости общего положения и горизонтально-проецирующей соответствует взаимной перпендикулярности этих плоскостей. Очевидно, перпендикулярность фронтальных следов фронтально-проецирующей плоскости и плоскости общего положения также соответствует взаимной перпендикулярности этих плоскостей.
Но если одноименные следы двух плоскостей общего положения взаимно перпендикулярны, то самые плоскости не перпендикулярны между собой. В заключение рассмотрим рис. 196. Здесь имеет место случай взаимной перпендикулярности одноименных следов в обеих их парах и перпендикулярности самих плоскостей: обе плоскости особого (частного) положения – профильная γ и профильно-проецирующая α
|
|
|
2. ПРЕОБРАЗОВАНИЕ ПРОЕКЦИЙ, ВРАЩЕНИЕ ВОКРУГ ЛИНИИ УРОВНЯ.
Этот способ применяется в основном для решения задачи преобразования плоскости общего положения в плоскость уровня. Суть способа заключается в том, что плоскость общего положения, поворачивается вокруг прямой уровня до состояния, параллельного горизонтальной плоскости проекций П1 либо фронтальной П2.
Рассмотрим поворот точки А вокруг горизонтали a до уровня горизонтали. Точка А движется по дуге окружности радиуса R с центром в точке O, принадлежащей горизонтали a. Радиус R является гипотенузой прямоугольного треугольника А0А1O, где один катет А1О – горизонтальная проекция радиуса вращения, другой – равен Dz – расстояние между точкой A и прямой a по вертикали. А' – новое положение точки А.
Алгоритм графических построений:
1) Через А1 проводим горизонтальную проекцию дуги по которой поворачивается точка А. Это будет прямая, перпендикулярная прямой a1;
2) На пересечении прямой a и проекции дуги отмечаем точку O1;
3) Строим прямоугольный треугольник A1A0O1. Попутно мы решили задачу нахождения расстояния между прямой и точкой. Отрезок A0O1 – расстояние от точки A до прямой a;
4) Обратите внимание, на то, что построения, выполняемые на верхнем демонстрационном чертеже выполняются в вертикальной плоскости, а на ортогональном чертеже мы делаем те же построения, только в горизонтальной плоскости. На результат построений такой прием не влияет;
5) Проводим дугу A0A1' с центром в точке O1. А1' – новая проекция точки А;
6) Подняв от A1' линию проекционной связи до пересечения с a2 находим A2'.
|
|
|
