 |
2. Проекции плоских углов. Рис 91 рис 92. 4. Если проекция некоторого угла, у которого одна сторона параллельна плоскости проекций, представляет собой прямой угол, то проецируемый угол тоже прямой
|
|
|
|
2. ПРОЕКЦИИ ПЛОСКИХ УГЛОВ.
1. Если плоскость, в которой расположен некоторый угол, перпендикулярна к плоскости проекций, то он проецируется на эту плоскость проекций в виде прямой линии.
2. Если плоскость прямого угла не перпендикулярна к плоскости проекций и хотя бы одна его сторона параллельна этой плоскости, то прямой угол проецируется на нее в виде прямого же угла.
3. Если проекция плоского угла представляет собой прямой угол, то проецируемый угол будет прямым лишь при условии, что, по крайней мере одна из сторон этого угла параллельна плоскости проекций.
4. Если проекция некоторого угла, у которого одна сторона параллельна плоскости проекций, представляет собой прямой угол, то проецируемый угол тоже прямой
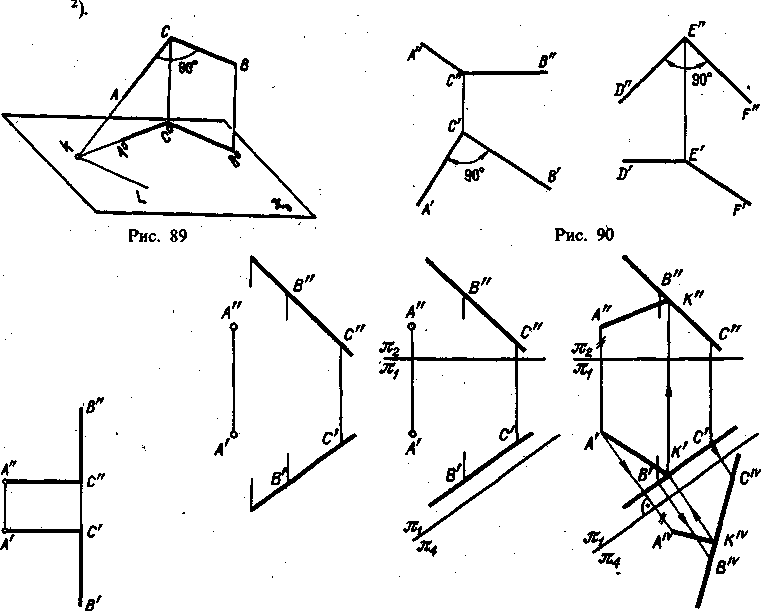
Рис 91 рис 92
5. Если плоскость тупого или острого угла не перпендикулярна к плоскости проекций и хотя бы одна сторона угла параллельна плоскости проекций, то проекция тупого угла на эту плоскость представляет собой тупой угол, а проекция острого угла - острый угол.
6. Если обе стороны любого угла, параллельны плоскости проекций, то его проекция равна по величине проецируемому углу.
Рис93 Рис 94
7. Если стороны угла параллельны плоскости проекций или одинаково наклонены к ней. то деление проекции угла на этой плоскости пополам соответствует делению пополам и самого угла в пространстве.
8. Деление угла в пространстве пополам соответствует делению пополам и его проекции только при условии, что стороны угла составляют с плоскостью проекций равные углы.
|
|
|
9. Если стороны угла одинаково наклонены к плоскости проекций, то угол-проекция не может равняться проецируемому углу.
рис 95 рис 96 
10. Проекции острого и тупого углов могут равняться проецируемому углу не только при условии параллельности сторон угла плоскости проекций.
Билет № 21.
1. ПОСТРОЕНИЕ РАЗВЕРТКИ ПОВЕРХНОСТИ МНОГОГРАННИКА СПОСОБОМ ТРИАНГУЛЯЦИИ.
Развертка многогранника представляет собой плоскую фигуру, полученную при совмещении всех его граней с плоскостью. Следовательно, построение развертки многогранника сводится к построению истинных величин его граней. Выполнение этой операции связано с определением натуральных величин его ребер, которые являются сторонами многоугольников - граней, а иногда и некоторых других элементов. Грани многогранника условно разделяются на боковые и стороны основания. Существуют три способа построения разверток многогранных поверхностей:
1) способ треугольников (триангуляции);
2) способ нормального сечения;
3) способ раскатки.
Построение развертки пирамиды способом триангуляции.
Общим методом построения разверток криволинейных поверхностей является метод триангуляции, при котором поверхность аппроксимируется (заменяется) вписанной или описанной многогранной поверхностью, грани которой – треугольники, а затем строится развертка многогранной поверхности, которая будет приближенной или условной разверткой криволинейной поверхности.
Этот метод применяется при построении развертки конической поверхности, которая аппроксимируется вписанной (реже описанной) пирамидальной поверхностью. Построение развертки конуса сводится к построению развертки пирамиды, у которой боковые грани являются треугольниками.
Метод триангуляции рационально использовать при построении развертки неразвертывающихся линейчатых поверхностей (цилиндроида, коноида, косой плоскости). При этом поверхность разбивают образующими на криволинейные четырехугольники, а затем в каждом четырехугольнике проводят диагонали, т. е. поверхность триангулируют. В этом случае поверхность аппроксимируется многогранной поверхностью, все грани которой треугольники.
|
|
|
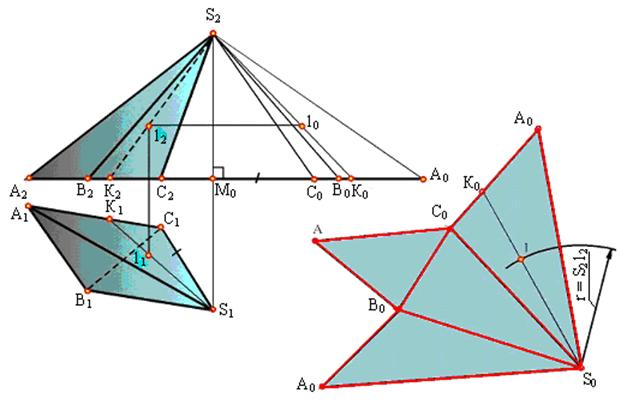
Изображенной на рисунке пирамиды стороны основания являются горизонталями и проецируются на плоскость П1 в истинную величину. Истинные величины боковых ребер определены способом прямоугольных треугольников. S2M0C0, S2M0B0 и S2M0А0, у которых одним катетом является высота пирамиды (S2М0 - разность высот точки S и точек А, В, С), а другим - горизонтальная проекция соответствующего ребра.
Натуральные величины ребер пирамиды могут быть определены способом вращения вокруг оси, проходящей через вершину S и перпендикулярной плоскости П1.
Следующая операция состоит в построении каждой боковой грани как треугольника по трем сторонам. В результате получается развертка боковой поверхности пирамиды в виде ряда примыкающих друг к другу треугольников с общей вершиной S. Присоединив к полученной фигуре основание ( АВС), получим полную развертку пирамиды. Построение на развертке точки 1, принадлежащей поверхности пирамиды, понятно из чертежа. Такой способ построения развертки поверхности называется способом триангуляций.
|
|
|
