 |
Модальные регляторы состояния
|
|
|
|
Рассмотрим объект несколькими входами, дискретная модель которого описывается РУ состояния
 ; (1)
; (1)
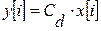 .
.
Предположим, что все собственные значения 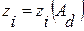 ,
,  вещественны и различны.
вещественны и различны.
Используя преобразование подобия
 или
или  (2)
(2)
получим

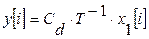
Теперь, умножив на матрицу T слева, получим
 (3)
(3)
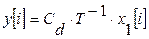
Если обозначить  ;
;  ;
;  ,
,
то РУ (3) примем вид
 ; (4)
; (4)
 .
.
В качестве преобразований подобия для оговоренного случая можно выбирать такие, что преобразованная матрица системы станет диагональной, т.е.
 (5)
(5)
Характеристическое уравнение исходной модели
 (6)
(6)
для преобразованной модели характеристическое уравнение имеет вид
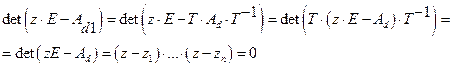 (7)
(7)
Перепишем (5) в виде
 или
или  (8)
(8)
Матрицу  можно рассматривать в виде векторов-столбцов
можно рассматривать в виде векторов-столбцов
 (9)
(9)
Теперь выражение (8) можно рассматривать так
 (10)
(10)
Для каждого столбца равенства (10) можно получить
 ,
,  (11)
(11)
или
 ,
,  (12)
(12)
Матричное уравнение (12) развертывается скалярным уравнением для n неизвестных векторов  , состоящих из координат
, состоящих из координат 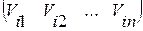 . Особенность уравнения (12) состоит в том, что оно однородно, поэтому, если
. Особенность уравнения (12) состоит в том, что оно однородно, поэтому, если  есть его решение, то и
есть его решение, то и  ,
,  также решение. Для выбора одного решения требуются дополнительные условия. Векторы
также решение. Для выбора одного решения требуются дополнительные условия. Векторы 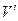 называют собственными векторами матрицы Аd. Они удовлетворяют уравнению (11). Для объектов с одним входом и одним выходом представление в пространстве состояний в диагональной форме соответствует разложение дискретной ПФ
называют собственными векторами матрицы Аd. Они удовлетворяют уравнению (11). Для объектов с одним входом и одним выходом представление в пространстве состояний в диагональной форме соответствует разложение дискретной ПФ 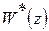 по «n» собственным значениям.
по «n» собственным значениям.
 (13)
(13)
Из разложения непосредственно видно, что значения коэффициентов  нельзя определить однозначно. Если задаться, например
нельзя определить однозначно. Если задаться, например  ,
,  , то теперь
, то теперь  (14)
(14)
Матрица λ может иметь не только действительные, но и комплексно-сопряженные значения  .
.
В этом случае можно поступить следующим образом:
1. Вводится вектор  (
(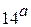 )
)
|
|
|
Уравнение (4) пример вид
 (15)
(15)
2. Рассматривается управление
 (16)
(16)
Получается РУ
 (17)
(17)
3. Если матрица ОС 
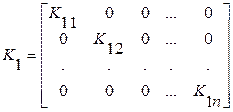 (18)
(18)
также диагональна, то результирующее характеристическое уравнение замкнутой системы будет иметь вид
 (19)
(19)
Собственные значения  ,
,  объекта теперь изменены независимо друг от друга. За счет выбора
объекта теперь изменены независимо друг от друга. За счет выбора  ,
,  , поскольку матрицы
, поскольку матрицы 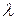 и
и  – диагональны.
– диагональны.
Вектор  реального управления вычисляется следующим образом
реального управления вычисляется следующим образом
 (20)
(20)
Так как согласно (20) необходимо обращать матрицу 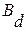 , то она должна быть регуляторной (квадратной) и
, то она должна быть регуляторной (квадратной) и  . Это означает, что n собственных значений
. Это означает, что n собственных значений  матрицы
матрицы  или
или 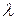 можно изменять независимо друг от друга только тогда, когда в объекте имеется n независимых входов, т.е. число управляющих координат
можно изменять независимо друг от друга только тогда, когда в объекте имеется n независимых входов, т.е. число управляющих координат  ,
,  равно порядку объекта.
равно порядку объекта.
Блок-схема системы с модальным регулятором по состоянию имеет вид

Модальный Модальный Модальный синтезатор регулятор анализатор
Переменные состояния 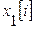 развязаны за счет преобразования модальным анализатором. Вектор
развязаны за счет преобразования модальным анализатором. Вектор  преобразованного управления формируется в модальном регуляторе
преобразованного управления формируется в модальном регуляторе  . Истинное управление
. Истинное управление  восстанавливается из преобразованного модальным регулятором. Следует заметить, что объекты, у которых имеется n управляющих входов, встречаются крайне редко. Чаще всего объекты имеет m-входов
восстанавливается из преобразованного модальным регулятором. Следует заметить, что объекты, у которых имеется n управляющих входов, встречаются крайне редко. Чаще всего объекты имеет m-входов  . Следовательно, матрица B имеет размер
. Следовательно, матрица B имеет размер  . Следовательно независимо могут быть изменены только m собственных значений
. Следовательно независимо могут быть изменены только m собственных значений  ,
, 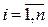 матрицы
матрицы  объекта. Остальные
объекта. Остальные 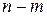 собственных значений, останутся прежними.
собственных значений, останутся прежними.
Рассмотрим объект, где  (один вход) его преобразованное уравнение
(один вход) его преобразованное уравнение
 (21)
(21)

Здесь  ,
, 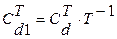 (22)
(22)
Для управления этим «преобразованным» объектом используется ОС по состоянию
 (23)
(23)
Подставив выражение для  в (21) получим
в (21) получим
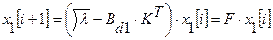 (24)
(24)
Если для исходного описания выбрано преобразование, в результате которого все элементы  , то
, то
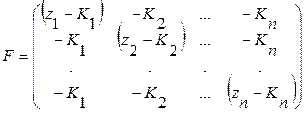 . (25)
. (25)
В этом случае отдельные координаты состояния уже не будут развязаны и собственные значения  матрицы F в отличии от матрицы λ будут изменяться взаимосвязано. Поэтому ОС по состоянию в данном случае не дает преимуществ модального управления. Если формировать ОС только по одной переменной
матрицы F в отличии от матрицы λ будут изменяться взаимосвязано. Поэтому ОС по состоянию в данном случае не дает преимуществ модального управления. Если формировать ОС только по одной переменной  , т.е.
, т.е.
|
|
|
 ,
,
то изменится только одно собственное значение  ,
,  остальные собственные значения
остальные собственные значения 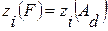 ,
,  ,
,  согласно матрице
согласно матрице

Характеристическое уравнение, соответствующее этой матрице,
 =0
=0
Выше, для упрощения, предлагалось, что все собственные значения  ,
,  матрицы
матрицы  различны. Если объект имеет кратные собственные значения, то вместо диагональной формы λ следует использовать жорданову форму.
различны. Если объект имеет кратные собственные значения, то вместо диагональной формы λ следует использовать жорданову форму.
|
|
|


