 |
Регуляторы состояния с конечным временем установления
|
|
|
|
Рассмотрим управляемый объект порядка n с одним входом
(1)
Ранее было показано, что объект может быть переведен из произвольного начального состояния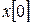 
в начало координат 
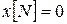за 
шагов (апериодический регулятор). Необходимая последовательность 
, 
управляющих воздействий может быть сформирована с помощью ОС по состоянию
(2)
В результате получим
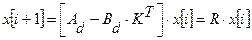(3)
теперь
; 
;…; 
(4)
Из условия 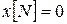следует чтобы 
(5)
Рассмотрим характеристическое уравнение замкнутой системы
(6)
Каждая матрица удовлетворяет условию характеристическому уравнению (теория Кели-Гамильтона), т.е.
Уравнение (4) удовлетворяется при ; 
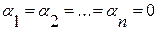
Характеристическое уравнение примет вид
Наличие полюса в начале координат кратности n является признаком системы управления с конечным временем длительности переходного процесса.
Если объект представлен РУ в канонической форме управляемости 
, то апериодический регулятор состояния можно получить, задавая 
, т.е.
При использовании канонической формы наблюдаемости 
структура объекта принимает вид, показанный на рисунке
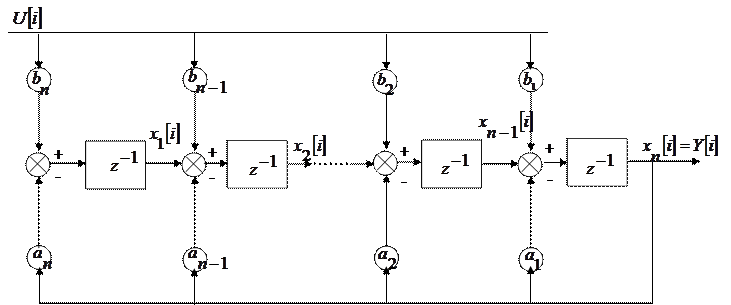
РУ имеет вид
Каждая из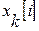 
, 
умножается на коэффициент 
, 
и заводится как ООС на вход объекта. Такой апериодический регулятор приводит объект из произвольного начального состояния 
за n-тактов к постоянному значению
при постоянном входе
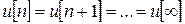
Поэтому такой регулятор называют «апериодическим регулятором выхода»
Наблюдатели состояния
Поскольку все координаты 
, вектора 
состояния для большинства объектов не могут быть непосредственно измерены, их приходится вычислять по данным некоторых измерений.
Рассмотрим объект
, (1)
.
Предположим, что в объекте можно измерить точно только:
|
|
|
1) вектор выхода 
;
2) вектор входа 
.
остальные координаты следует вычислять.
Вычислитель координат состояния называют наблюдателем состояния.
В качестве модели наблюдателя используется в данном случае РУ (1). В результате модель объекта с наблюдателем имеет вид
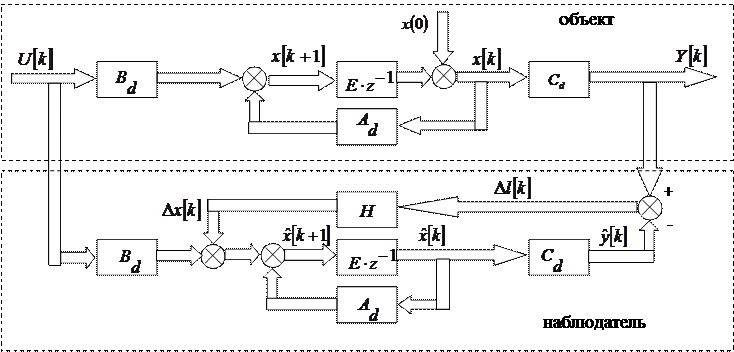
Из рисунка видно, что наблюдатель имеет ту же структуру, что и объект. Разность выходов 
(2) объекта и наблюдателя, умноженная на матрицу Н, используется в качестве обратной связи для подгонки 
. Если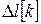 
станет равным 0, то станет 
. Такая модель наблюдателя называется Льюинбергера.
Динамические свойства наблюдателя зависят от матрицы Н. Она должна выбираться так, чтобы вектор состояния наблюдателя 
асимптотически сходился к вектору состояния объекта, т.е. 
, при 
. Из рисунка следует, что
(3)
Вектор ошибки оценки состояния равен
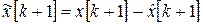(4)
Вычитая уравнение (3) из (1), получим РУ
(5)
Таким образом, ошибка задается решением однородного РУ (5). Ее значения зависят от значения начальной ошибки 
и не зависят от входного сигнала 
. (Это возможно только тогда и только тогда, когда РУ (1) объекта и РУ (3) наблюдателя имеют одинаковые матрицы 
и 
, 
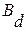. Практически модель (1) никогда не может быть полностью адекватна объекту. Но при теоретических исследованиях принятая гипотеза оправдана.
Для того чтобы процесс сходился, необходимо, чтобы
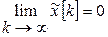
Требуется, чтобы характеристическое уравнение
именно корни 
, внутри окружности единичного радиуса, т.е. 
, . Это условие можно осуществить за счет выбора соответствующей матрицы H наблюдателя.
Одна методика выбора матрицы Н состоит из следующих действий.
Используется свойство определителей матриц
.
На его основании имеем
(6)
Это позволяет от уравнения (3) наблюдателя перейти к более удобному уравнению, когда заменяются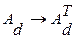 
, 
, 
.
Вместо модели (1) объекта
При управлении с ОС
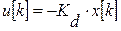
рассмотрим «дополнительный» объект
(7)
с обратной связью
(8)
|
|
|
Теперь матрицу Н наблюдателя можно выбирать различными способами. Один из них следующий:
1) определение характеристического уравнения
, (9)
как уравнения с заданными значениями корней.
Для одномерного объекта, когда и 
– скаляры, то матрица Н станет вектором-столбцом h из n координат. Уравнение наблюдателя примет вид
(10)
Здесь удобно использовать каноническую форму наблюдаемости вместо канонической формы управляемости. Таким образом:
(11)
Отсюда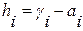 
, , где 
– коэффициенты желаемого характеристического многочлена 
.
Второй способ определения характеристического уравнения (4) заключается в том, что
2) все 
, . Поэтому при 
,
получим наблюдатель с минимальной длительностью переходного процесса равной 
(как и в случае с апериодическим регулятором).
3). Параметры характеристического уравнения выбираются из условия минимизации квадратичного критерия качества. (не рассматривается этот случай)
Таким образом, характеристики наблюдателя можно выбирать различными способами. Разумеется, разным характеристикам соответствуют и разные решения однородного РУ (5).
При практической реализации наблюдателей возникают различные затруднения.
1. Шумы, неизбежно присутствующие в сигналах, не позволяют сделать наблюдатель с конечной длительностью переходного процесса за .
2. Рассмотренный выше наблюдатель предназначен для оценки всех координат , вектора состояния объекта. Однако на практике некоторые из координат 
, 
можно измерить непосредственно соответствующими датчиками. Например, выходной сигнал системы часто является одной из координат состояния. В таком случае оценке путем вычисления подлежат только остальные не измеряемые координаты состояния. В такой ситуации требуется наблюдатель пониженного порядка (их не рассматриваем).
|
|
|
