 |
Вводная часть второго урока
|
|
|
|
Урок 1-4 «Сначала займёмся повторением.
Самостоятельная работа»
Предметные задачи:
- повторение основных вопросов программы 3-го класса: письменная нумерация многозначных чисел; поразрядное сравнение многозначных чисел; правило деления на «круглое» число; приёмы устного деления двузначного числа на двузначное; разностное и кратное сравнение чисел и величин; вычисление значения выражения, порядок действий; способы умножения многозначного числа на однозначное число и многозначного числа на двузначное число столбиком; геометрический материал: вычисление периметра и площади прямоугольника, измерение площади прямоугольника с помощью палетки; формулирование задачи по краткой записи, составленной в виде таблицы и на основании данного решения, представление данных в виде диаграммы сравнения; нахождение рационального пути решения задачи; усвоение нового: установление того, что прямоугольники могут иметь одинаковую площадь, но разный периметр;
Формирование УУД: Познавательные: выполнение заданий с помощью таблиц, выбор наиболее рационального способа решения задачи. Регулятивные: умение определять задачи урока, анализировать достигнутые результаты Коммуникативные: умение излагать своё мнение и аргументировать свою точку зрения, управлять действиями партнёра Личностные: ориентация на самоанализ и самоконтроль результата, на анализ соответствия результатов требованиям конкретной задачи, на понимание предложений и оценок учителей, товарищей
Пропедевтика: решение задач на «сумму и разность» и задач на «сумму и частное»
Методы и приёмы организации деятельности учащихся: беседа с целью воспроизведения и расширения ранее изученного материала (понятий, правил), самостоятельная работа учащихся по учебнику и тетради для самостоятельных работ.
|
|
|
Учебно-методическое обеспечение: У – 1, Т – 1, линейка, простой карандаш, угольник, таблица с темами для повторения
Ход урока
Вводная часть первого урока
– Сообщаем учащимся, что первые уроки по математике посвятим повторению.
– Предлагаем просмотреть задания № 1 – № 7, далее в своих таблицах отметить R темы для повторения на первом уроке.
| Темы для повторения | |
| Поразрядное сравнение многозначных чисел | R |
| Вычисление периметра и площади прямоугольника | |
| Выбор рационального пути решения задачи | |
| Разностное и кратное сравнение чисел | R |
| Разностное и кратное сравнение величин | |
| Вычисление значения выражения, порядок действий. | R |
| Измерение площади прямоугольника с помощью палетки | |
| Правило деления на «круглое» число | R |
| Представление данных в виде диаграммы сравнения | |
| Формулирование задачи по краткой записи, составленной в виде таблицы или по предложенному решению | |
| Способы умножения многозначного числа на однозначное число и многозначного числа на двузначное число столбиком | R |
Продолжение урока
Задание № 1, 2 (У – 1, с.7)
– Предлагаем ученикам с помощью разрядной таблицы записать шестизначное число, каждая цифра записи которого совпадает с номером разряда, следующего за разрядом, в котором она находится(765432)
| Разряд сотен тысяч | Разряд десятков тысяч | Разряд единиц тысяч | Разряд сотен | Разряд десятков | Разряд единиц |
– Предлагаем учащимся придумать подобные задания и предложить для выполнения в классе. Например, записать пятизначное число, каждая цифра записи которого совпадает с номером разряда, в котором она находится(54321)
|
|
|
– Просим учащихся с помощью разрядной таблицы записать самое большое шестизначное число, в записи которого три раза встречается цифра 1.
– Вспоминаем, что наибольшее число получится только тогда, когда, начиная со старшего разряда, все разряды заполняться самыми большими возможными числами.
– Учащиеся конструируют искомое число.
Ожидаемый ответ: В первых трёх старших разрядах можно записать цифру 9. В оставшихся трёх разрядах нужно записать цифру 1, так как другой возможности использовать три раза цифру 1 уже не будет. Если же цифру 1 записать ранее, то полученное шестизначное число будет меньше, чемто, запись которого начинается с трёх девяток.
– Делаем вывод, что искомое число 999111.
Задание № 3 (У – 1, с.7) Учащиеся читают задание.
– Выясняем, что нужно составить и записать пары чисел, каждая из которых состоит из пятизначного и шестизначного числа, а результат разностного сравнения чисел в паре равен 5.
– Обращаем внимание учащихся на то, что все эти пары будут располагаться вблизи границы, разделяющей на числовом луче пятизначные и шестизначные числа, и предлагаем, вспомнить наименьшее шестизначное число (100000) и наибольшее пятизначное число(99999). – Предлагаем учащимся начать конструирование искомых пар. – Организуем проверку на доске: 100000 и 99995; 100 001 и 99996; 100002 и 99997; 100003 и 99998; 100004 и 99999.
Задание № 4 (У – 1, с.7)
– Сами читаем первую часть задания: выполни кратное сравнение между следующими разрядными единицами: 1000 и 10.
– Вспоминаем, что выражение, с помощью которого можно узнать восколько раз одно число отличается от другого называется кратнымсравнением.
– Просим учащихся самостоятельно выполнить кратное сравнение между разрядными единицами 1000 и 10.
–Проверяем на доске:
1000: 10 = 100
– Читаем вторую часть задания: составь и запиши ещё четыре пары разрядных единиц с таким же результатом кратного сравнения.
– Записываем на доске выражения, которые предлагают учащиеся:
10000: 100 = 100
100000: 1000 = 100
1000000: 10000 = 100
Примечание: Может возникнуть трудность с тем, что такие числа мы пока не рассматривали. Но если учащиеся назовут числа более миллиона правильно, можно записать и их. Например, 10000000: 100000 = 100.
|
|
|
– Делаем вывод, что для получения такого же результата кратного сравненияможно уменьшить делимое и делитель в одно и то же число раз.
– Выясняем, что делимое и делитель пары разрядных единиц 1000: 10 = 100
можно уменьшить в 10 раз. Записываем получившееся равенство: 100: 1 = 100.
– Задание № 5 (У – 1 с. 7)
– Предлагаем учащимся устно вычислить значение следующего выражения: (45863 + 75981): (75981 + 45863) – (982564 - 982560) Рассуждаем так: значение выражений, записанных в первых двух скобках, равны (45863 + 75981= 75981 + 45863 - переместительное свойство), значит, не выполняя вычислений, можно сказать - результат деления числа на само себя равен 1.
Остаётся вычислить значение разности в третьей скобке (4) и выполнить умножение (1 – 4 = 4).Значение данного выражения равно 4.
Задание № 6 (У – 1, с.7)
– Предлагаем устно вычислить значение первого выражения:
983657 – (983657 – 144)
– Обращаем внимание учеников на уменьшаемое 983657 и вычитаемое 983657 – 144. Вычитаемое на 144 меньше уменьшаемого. Это позволяет легко найти значение выражения (144)
– Вспоминаем, какие правила будут использованы при вычислении значения выражения: 14400: 100 – (569873 – 569872)
Ожидаемый ответ: правило деления на «круглое» число, правило умножения числа на 1.
– Учащиеся устно вычисляют значение выражения (144)
– Далее просим учащихся выполнить 3 – часть задания – составить и записать равенство или неравенство данных двух выражений, устно
проверяя его: 983657 - (983657 – 144) = 14400: 100 – (569873 – 569872)
Задание № 7 (У – 1, с.8)
– Предлагаем учащимся сначала самостоятельно выполнить умножение многозначного числа на однозначное число, а затем многозначного на двузначное столбиком (пауза)
– Одновременно вызываем к доске 2 – х учеников, которые работают с нашей помощью.


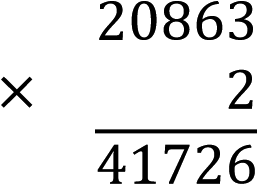

Задание на дом: № 3 (Т – 1, с. 3)
Вводная часть второго урока
– Предлагаем просмотреть задания № 8 – № 15 и продолжить заполнение таблицы, начатой на первом уроке.
| Темы для повторения | |
| Поразрядное сравнение многозначных чисел | R |
| Вычисление периметра и площади прямоугольника | R |
| Выбор рационального пути решения задачи | |
| Разностное и кратное сравнение чисел | R |
| Разностное и кратное сравнение величин | R |
| Вычисление значения выражения, порядок действий. | R |
| Измерение площади прямоугольника с помощью палетки | R |
| Правило деления на «круглое» число | R |
| Представление данных в виде диаграммы сравнения | |
| Формулирование задачи по краткой записи, составленной в виде таблицы или по предложенному решению | |
| Способы умножения многозначного числа на однозначное число и многозначного числа на двузначное число столбиком | R |
Продолжение урока
|
|
|
Задание № 8 (У – 1, с.8)
– Спрашиваем у учащихся, как вычислить периметр и площадь прямоугольника и предлагаем самостоятельно выполнить задание.
– Организуем проверку на доске:
Р = 5 см 5 мм – 2 + 3 см – 2 = (5 см + 5 мм) – 2 + 3 см – 2 = 10 см + 10 мм +
+ 6 см = 17 см
S = 5 см 5 мм – 3 см = (5 см + 5 мм) – 30 мм = 55 мм – 30 мм = 1650 кв.мм
Задание № 9 (У – 1, с.8)
– Учащиеся самостоятельно читают задание, чертят в тетрадях прямоугольники со сторонами 4 см и 3 см, 6 см и 2 см, находят их периметры и площади.
– Задаём вопрос.
– Могут ли прямоугольники иметь равные площади, но разные периметры? Ожидаемый ответ: периметр первого прямоугольника равен 14 см, периметр второго прямоугольника равен 16 см, при этом площадь каждого из них 12 кв. см. Значит, прямоугольники могут иметь одинаковую площадь, норазный периметр.
– Учащиеся читают задание и выполняют его аналогично предыдущему.
– Делаем вывод, что прямоугольники могут иметь одинаковый периметр, норазные площади.
Задание № 11* (У – 1, с.9)
– Просим учащихся прочитать задание и предлагаем составить план действий:
1. Найти длину стороны квадрата, периметр которого 32 см
2. Установить, на сколько дециметров нужно увеличить сторону квадрата, чтобы его периметр увеличился на 12 дм
3. Вычислить сторону «нового» квадрата
4. Вычислить площадь «нового» квадрата
5. Вычислить площадь «старого» квадрата
6. Выполнить разностное сравнение
– Далее учащиеся выполняют действия по плану, проводим пошаговую проверку:
1. Чтобы найти длину стороны квадрата, нужно его периметр разделить на 4. (32 дм: 4 = 8 дм)
2. Так как все четыре стороны квадрата имеют одинаковую длину, то чтобы узнать на сколько увеличится сторона квадрата, нужно 12 дм разделить на 4. (12 дм: 4 = 3 дм)
3. Вычисляем сторону «нового» квадрата (8 дм + 3 дм = 11 дм)
4. Вычисляем площадь «нового» квадрата» (11 дм – 11 дм = 121 кв. дм)
5. Вычисляем площадь «старого» квадрата (8 дм – 8 дм = 64 кв. дм) 6. Выполняем разностное сравнение (121 кв. дм - 64 кв. дм = 57 кв. дм) Делаем вывод, что площадь «нового» квадрата увеличится на 57 кв. дм.
|
|
|
Задание № 12 (У – 1, с.9)
– Предлагаем ученикам вспомнить, способ измерения площади прямоугольника с помощью палетки.
Ожидаемый ответ: для измерения площади прямоугольника нужно, совместить левый нижний угол палетки с левым нижним углом прямоугольника и посчитать количество квадратов с площадью 1 кв. см, которые уместились в данном прямоугольнике.
– Проводим устную проверку результатов измерений (15 кв. см)
Задание № 13 (У – 1, с.9)
– Учащиеся самостоятельно читают задание.
– Спрашиваем, на сколько минутных делений должна повернуться минутная стрелка, чтобы получился поворот на прямой угол?
Ожидаемый ответ: минутная стрелка повернётся на 15 делений.
– Выясняем, какую часть от 15 минут составляет 5 минут (Третью часть,
так как 15 мин: 5 мин = 3 раза)
– Делаем вывод, что угол поворота минутной стрелки на 5 минут составляет третью часть от прямого угла.
Задание № 14 (У – 1, с.9)
– Учащиеся самостоятельно читают задание, чертят квадрат со стороной 4 см, разбивая его на два прямоугольных треугольника.
– Выясняем, что равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью сторону основанием равнобедренного треугольника.
– Предлагаем учащимся составить из двух прямоугольных треугольников равнобедренный треугольник с основанием 8 см, начертить его в тетрадях. – Даём время на выполнение задания, просим учащихся доказать, что начерченный прямоугольник является равнобедренным.
| 8 |
| см |
Задание № 15* (У – 1, с.9)
– Записываем на доске формулу: S = a – b и просим учащихся, высказать предположения о том, какими могут быть длина и ширина прямоугольника, если его площадь равна 20 кв. см.
– Записываем предположения учеников на доске, предлагая проверить их. – Выясняем, что стороны прямоугольника могут быть 5 см и 4 см, 10 см и 2 см или 20 см и 1 см.
– Далее просим учащихся высказать предположения о том, как, зная длину сторон прямоугольника начертить треугольник с площадью 10 кв. см.
Ожидаемый ответ: если прямоугольники со сторонами 4 см и 5 см,
10 см и 2 см или 20 см и 1 см разделить на два равных прямоугольных треугольника, то площадь каждого из них будет равна 10 кв. см.
– Предлагаем ученикам начертить такой треугольник в тетрадях.
Задание на дом: № 4, 5 (Т – 1, с. 4)
|
|
|


