 |
Решение. По 2-му закону Ньютона mg + T = ma
|
|
|
|
Практические занятия нацелены на закрепление знаний, полученных при изучении теоретического материала.
1. Необходимо проработать решения приведенных ниже задач по механике и термодинамике.
2. Задачи по электричеству приведены в файле «Практическое занятие Электричество заочн. docx». Необходимо ознакомиться с содержанием приведенных задач и разобрать половину решений задач, приведенных в данном файле.
Решение задач
1. Перед разбором конкретных задач для повторения изученного материала приводятся определённые сведения, с которыми необходимо ознакомиться.
2. Прочитать и осмыслить условие задачи. Понять смысл физических величин известных по условию задачи и тех, которые предстоит отыскать. Если нет уверенности в правильной интерпретации смысла величин, необходимо обратиться к теоретическому материалу.
3. Перейти к разбору приведенного решения задачи. При необходимости обращаться к теоретическому материалу, изложенному на стр. 2 – 25.
4. Разбирать решения задач следует с авторучкой в руках, повторяя и осмысливая ход решения, повторяя рассуждения и выкладки решения, а не просто прочитывая текст по «диагонали». Только в этом случае решения задач действительно принесу реальную пользу, даже если не всё будет понято до конца и не все задачи будут проработаны.
Задача 1. Кинематическое уравнение движения материальной точки по прямой (ось Х) имеет вид х = А + Bt +Ct2 , где А = 4 м, В = 2м/с, С = -0, 5 м/с2 . Для момента времени t1 = 2 с определить 1) координату х1 точки; 2) мгновенную скорость V1; 3) мгновенное ускорение а1.
Решение. Координату точки в момент времени t1 найдем, подставив в уравнение исходные данные и произведя вычисления. Х1 = 4 м
|
|
|
Мгновенную скорость найдем, продифференцировав координату х по времени
V = 
В + 3Сt2 В момент времени t1 V1 = - 4 м/с (точка движется в отрицательном направлении координатной оси).
Мгновенное ускорение найдем, продифференцировав уравнение скорости по времени
а =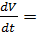 
6Сt В заданный момент времени а1 = - 6 м/с2
Задача 2. Груз массой m = 45 кг вращается на канате длиной l = 5, 0 м в горизонтальной плоскости, совершая n = 12, 0 об/мин (см. рис. ). Какой угол с вертикалью образует канат и какова сила его натяжения?
Решение. По 2-му закону Ньютона mg + T = ma
Так как движение по окружности происходит с постоянной скоростью, то полное ускорение тела – это нормальное ускорение, направленное к центру окружности радиуса R.
a = an = V2/R = 4p2n2R
Выберем оси X и Y (см. рис). Тогда проекции уравнения на оси
ОХ: T sina = m 4p2n2R (1)
OY: T cosa - mg = 0 (2)
Из чертежа видно, что R = l sina (3)
Решая совместно (1), (2), (3), получаем
T = 4p2n2m l a = arcos(g/ 4p2n2 l)
Числовая подстановка дает значения Т = 0, 64 кН, a = 45о
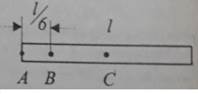Задача 5. Определить момент инерции J тонкого однородного стержня длиной l = 50 см и массой m = 360 г относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на 1/6 его длины.
Решение. Момент инерции стержня можно определить по теореме Штейнера:
Jв = Jc + ma2,
где Jс – момент инерции стержня относительно центра масс (т. С), а = ВС
Jв = m l 2/12 + m(1/2 – 1/6)2 = 7m l 2/36
Сделав числовую подстановку, находим Jв = 1, 75 10-2 кг м2
Задача 6. Круглая платформа радиусом R = 1, 0 м, момент инерции которой J = 130 кг м2, вращается по инерции вокруг вертикальной оси, делая n1 = 1, 00 об/с. На краю платформы стоит человек, масса которого m = 70 кг. Сколько оборотов в секунду n2 будет совершать платформа, если человек перейдет в ее цент? Момент инерции человека рассчитать как для материальной точки.
Решение. Для системы человек-платформа выполняется закон сохранения момента импульса:
|
|
|
L1 = L2
Рассчитаем эти моменты
Человек находится на краю платформы L1 = J1w1 = (J + mR2) 2pn1
Человек находится в центре платформы L2 = J2w2 = J 2pn2
Решая систему уравнений, находим n2 = n1(J+mR2)/J
Подставив числовые значения, находим n2 = 1, 5 об/с.
Задача 7. Какое количество кислорода выпустили из баллона емкостью V = 10, 0 л, если при этом показания манометра изменились с 14, 0 до 7, 0 ат, а температура понизилась от t1 = 27оС до t2 = 7оС.
Решение. Масса выпущенного кислорода Dm равна разности между начальной массой m1 кислорода в баллоне и конечной m2
Dm = m1 - m2
Так как условия в баллоне не отличаются от нормальных, воспользуемся уравнением состояния идеального газа
p1V = m1RT1/µ p2V = m2RT2/µ
Из данных уравнений получим Dm = µV(p1/T1-p2/T2)/R
Подставив числовые значения в системе СИ и учитывая, что у кислорода µ = 0, 032 кг/моль, рассчитаем Dm = 95 г
|
|
|
