1.6. Движение материальной точки по окружности

1. 6. Движение материальной точки по окружности

 

Для описания движения материальной точки по окружности вводятся угловые характеристики движения.

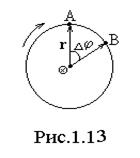
Угловым перемещением D 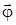 называется вектор, численно равный углу поворота радиуса - вектора за промежуток времени Dt и направленный вдоль оси вращения так, чтобы из конца его вращение было видно происходящим против часовой стрелки (рис. 1. 13).

Радиус-вектор  - это вектор, проведенный из центра окружности в рассматриваемую точку А.

Направление вектора D 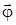  определяется по правилу правого винта (рис. 1. 14).

Единицей измерения D 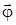  является радиан.

Мгновенной угловой скоростью называется векторная величина равная

  .

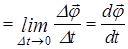Единицей измерения wявляется рад/с или с^-1.

Вектор направлен вдоль оси вращения по правилу правого винта также, как и вектор D 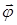(рис. 1. 15).

Если  = const, то движение точки равномерное по окружности                             

 =

и его можно характеризовать периодом Т - временем, за которое точка совершает один полный оборот, и частотой вращения n - величиной равной числу полных оборотов за единицу времени и обратной периоду вращения

n = 1/T,

w = 2pn,

 w = 2p/T.

Кинематическое уравнение равномерного движения    

j = j₀ ± wt.

Мгновенным угловым ускорением называется векторная величина, равная

 .  

Единицей измерения e является рад/с² или с^-2.

Если 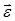 = const, то движение точки равнопеременное и

 

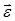
Кинематические уравнения равнопеременного движения точки по окружности                       

Связь между линейными и угловыми характеристиками движения

 

v = w r;   v = 2pnr;

a_t= e r;    a_n = w²r = 4p²n ² r = .

 

II. Динамика материальной точки

2. 1. Законы Ньютона. Масса тела. Сила

 

Раздел механики, в котором изучают причины появления ускорения тел, а также рассматриваются способы его вычисления, называют динамикой.

Основу динамики материальной точки составляют три закона Ньютона.

Первый закон Ньютона: существуют такие системы отсчета (инер-циальные), относительно которых материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние

 = const, если   = 0.

Второй закон Ньютона: в инерциальной системе отсчета сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение

= m .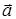

Третий закон Ньютона: две материальные точки действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны вдоль прямой, соединяющей эти точки

₁₂ = - ₂₁,

где ₁₂ - сила, действующая на первое тело со стороны второго, и ₂₁ - сила, с которой первое тело действует на второе (рис. 2. 1).

Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.

В разделе динамики вводятся понятия: масса и сила.

Масса - это количественная мера инертности тела при поступательном движении.

Сила - это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или деформацию или то и другое.

 

Принцип независимости действия сил

(принцип суперпозиции)

Если на материальную точку массой m одновременно действуют несколько независимых между собой сил ₁, ₂, ₃, . . . _n, то каждая из этих сил сообщает материальной точке ускорение, величина и направление которого не зависит от действия других сил.

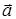    = ( ₁, ₂, ₃, . . . _n) /m = /m.

Механический принцип относительности Галилея

 

Никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить, покоится она или движется равномерно и прямолинейно.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: